改进粒子群算法在电力系统无功优化中的应用

熊军华 赵臣鹏 张翠影 王亭岭 曾 浩

（华北水利水电大学，河南 郑州 450011）

0 引言

美国社会心理学家J.Kennedy 和电气工程师R.Eberhart 在1995年提出粒子群算法（PSO）[3]，该算法根据仿生学的研究，尤其对兽群等群体活动的模仿，并结合生物学家F.Heppner 的生物群体模型及进化计算的思想，是一种高效的优化计算方法。粒子群算法具有容易实现、收敛性好及计算结果精确等优点[2]，适合解决非线性、多维数、有约束的复杂优化问题，因此近些年被广泛应用到电力系统无功优化、电力系统状态估计以及电力系统电压控制等方面。

1 标准粒子群算法及改进

1.1 标准的粒子群算法

标准PSO 算法：各个待优化问题的可能解可以抽象为解空间中的一个粒子，全部粒子有一个被目标函数指定的适应量；由N 个粒子构成的粒子群在m 维空间中进行搜索，各个粒子的绝对位置为xi=(xi1，xi2，…，xim)，各个粒子的绝对速度为vi=(vi1，vi2，…，vim)。在任何一次迭代中，粒子所跟踪的个体历史最优位置pm和整个粒子群的最优解pg来更新自己。更新公式为：

其中：t 为迭代次数；c1、c2为学习因子；r1、r2为介于[0，1]间的随机常数；ω 为惯性权重系数且在迭代过程中线性递减，其计算的公式如下：

其中：tmax为最大的迭代次数；ωstart和ωend分别为初始惯性权重系数和终止惯性权重系数。

1.2 改进的粒子群算法

引入共轭梯度的方法[4]，在计算过程中若陷入局部的最优解，则把该局部极值视为共轭梯度法的初始点。设待优化的问题为minf(x)，给出一个初值x1[5]，根据目前已知点的梯度确定搜索方向，计算下一个解。在第k 次迭代时，目前迭代点为xk，搜索方向为dk∈Rn，记梯度为g(x)=Δf(x)，共轭梯度法的公式如下：

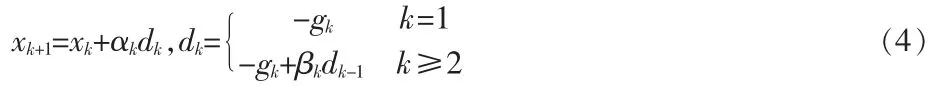
其中：αk为步长因子。从xk沿dk寻找一个好的点作为下一个迭代点，即：

其中：α＞0，参数βk满足下式条件：

2 电力系统无功优化数学模型

电网无功优化是具有多变量、多约束条件等特点的非线性优化问题[6]，主要通过调节发电机端电压、补偿电容切投容量、功率潮流分布以及可调变压器分接头档位来进行优化。

目标函数是系统有功损耗。

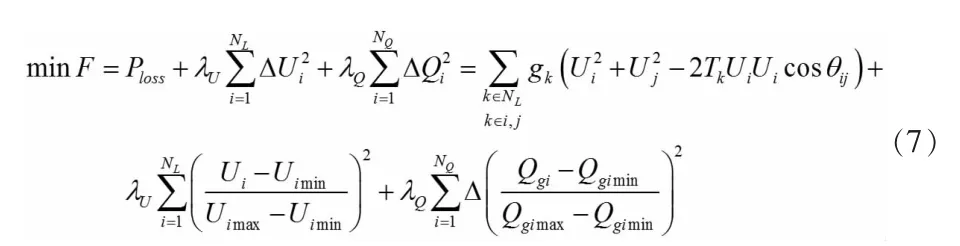
其中：Ploss为系统的有功损耗；Ui与Uj为负荷节点i 与j 的电压幅值；ΔQi与λQ分别为发电机无功越限值及其惩罚系数；ΔUi与λU分别为电压越限值及其惩罚系数；θij为负荷节点i、j 之间电压相位角；gk为支路k 的电导；Tk为电压器k 的变比；NL为系统节点数。

3 算法的实现

共轭梯度法的粒子群算法的具体步骤如下：

1）输入无功优化需要的原始数据和PSO 算法参数，初始化粒子的位置和速度；

2）评价每个粒子，潮流计算得到每个粒子的适应值，将该值与个体极值进行对比；

3）用式（1）、式（2）更新粒子位置和速度；

4）判断算法是否陷入停滞，如算法陷入局部最优，设此时的最优解为X；

5）以作为共轭梯度法的初始点，用共轭梯度法进行计算，得到的解为X；

6）判断算法是否结束，如是否达到最大迭代次数，是则停止运行输出结果，若不满足，则以为整个粒子群的最优解转至步骤2 继续计算。

4 结语

改进的粒子群优化算法比标准粒子群算法收敛速度快，求得无功优化结果更为精准，网络损耗也显著下降，极大地提高电压水平，使得系统供电更加经济有效，说明改进粒子群算法更适合解决电力系统复杂的无功优化问题。

［1］朱太秀.电力系统优化潮流与无功优化[J].电网技术，1990，14(4)：23-25.

［2］刘方.电力系统动态无功优化模型及混合算法的研究[D].重庆：重庆大学，2003.

［3］Shigenori Naka，Takamu Genji.A hybrid particle swarm optimization for distribution state estimation[J].IEEE Trans on Power Systems，2003，18(1)：60-68.

［4］袁晓辉，王乘，张勇传.粒子群优化算法在电力系统中的应用[J].电网技术，2004，28(19)：14-19.

［5］阳春华，谷丽姗，桂卫华.自适应变异的粒子群优化算法[J].计算机工程，2008，34(16)：188-120.

［6］王向臣.电网无功补偿实用技术[M].北京：中国水利水电出版社，2009：235-401.

［7］IEEE Committee Report.IEEE reliability test system[J].IEEE Trans PWRS，1979，98(6)：2047-2054.