基于GIS的长大引水线路优选的方法研究

余 国 谢谟文 王立伟

（北京科技大学土木工程系，中国 北京 100083）

0 引言

对长大引水线路工程地质条件复杂性、地质参数的不确定性，引水工程在施工过程中可能会存在突水、突泥等重大工程地质问题，而且也有可能引起区域岩溶地下水疏干而导致重大社会环境问题。传统的线路方案选择仅仅是由单个影响因素或几个因素各自直观地评价而确定，带有极大的经验成分，容易受到经验的影响而不能正确反映实际情况。

针对这些问题，许多学者进行了深入研究，如鲍新华等提出比选法与层次分析法在引水线路有选中的应用[1]，徐学军等提出模糊综合评价法在引水线路优选中的应用[2]，提出了综合考虑多个因素的线路优选方法。本文以滇中引水工程香炉山段的引水线路优选问题为研究对象，基于遥感技术、GIS 技术[3-4]，用层次分析法通过剖析影响长大引水线路优选方案决策的各种定性和定量因素，建立综合评判优选栅格模型[5]，从而确定最优的长大引水线路方案。

1 层次分析法模型的建立

1.1 层次分析法的基本原理

层次分析法（Analytic Hierarchy Process，简称AHP）是一种利用数学分析，把分析指标层次化、数量化，并且把定性指标定量化分析的方法。它可以把一些虽然独立，但是相互制约的影响因素综合起来考虑，并把这种综合用数值的方法显示出来。

采用“专家打分一层次分析法”来确定权重，得出判断矩阵，接着把每个专家构建的判断矩阵集中得到综合判断矩阵，最后应用方根法求权重。再结合工程实例，分析和计量影响因素的性状数据，计算出各方案的综合得分，应用于决策。

主要分析、评价的步骤如下：

（1）在分析影响因子的基础上，根据影响度不同和因子之间的隶属关系构建评价层次结构；

（2）确定各层次机构中影响因子之间的相关关系，构造判断矩阵；

（3）确定各因子的影响权重，进行层次单排序及一致性检验；

（4）根据层次单排序及层次结构确定层次总排序并进行一致性检验。

1.2 评价层次结构的建立

在对拟建该区域详细调查和深入研究的基础上，综合分析地质特点、生态环境特征和工程建设要求，利用层次分析法基本原理，可建立该区引水线路方案综合评价指标（U）体系，见图1。

1.3 判断矩阵的构造

在建立了图1 所示的综合评价指标体系后，可运用层次分析法确定各因素的权重分配问题。采用Satty 教授提出的1～9 级标度法给予数量标度[6]，从第2 层开始，对上一层某个元素与下一层相关的元素，进行两两对比，按其重要程度等级，得到由aij构成的n×n 阶矩阵即为判断矩阵：

式中，aij为因子i 相对因子j 的重要性。

图1 综合评价指标体系Fig.1 Index system for synthesis evaluating project

1.4 层次单排序及一致性检验

层次单排序是据判断矩阵去推算本层次所有元素对上一层次某一元素而言的权重。假设有一n 阶正规向量W∶AW=λmaxW，其中λmax为矩阵A 的最大特征根，W 为对应λmax的正规化特征向量。可采用方根法近似计算A 的特征值λmax和特征向量W[7]。

为使判断结果更好地与实际状况相吻合，需进行一致性检验。评价判断矩阵一致性的检验指标为:CR=CI/RI。其中CI为一致性检验指标，CI=(λmax-n)/(n-1)；n 为判断矩阵的阶数；RI为平均随机一致性指标，取值见表1。

表1 随机一致性指标表[8]Tab.1 Values of average stochastic coincidence indicators

1.5 层次总排序及一致性检验

从层次结构模型的第2 层开始，逐层计算各层相对于最高层(目标层)相对重要性的排序权值，称为层次总排序。假设第k 层包含m 个因素A1，A2，…，Am，相应的层次总排序权值分别为a1，a2，…，am；第k+1层包含n 个因素B1，B2，…，Bn，它们对影响因素Aj(j=1，2，…，m)的层次单排序为β1j，β2j，…，βnj；则第k+1 层因素Bi的层次总排序权值为：

层次总排序也需要进行一致性检验，公式为：

当CR＜0.1 时，该层次总排序计算结果具有满意的一致性。

1.6 计算权重向量

根据线性代数里求解特征向量和特征根的方法，利用如下方程式求解：

AW=λmaxW （4）

式中λmax为最大特征值，W 为对应于最大特征值的特征向量。W即为该层次的权重集。

1.7 综合评价

各个选线因子的对线路影响程度的分级栅格模型及综合权重，构建综合评判优选栅格模型，得出各个方案的评价指标值，选出最优方案。

2 工程实例分析

2.1 工程概况

滇中是云南省国民经济社会发展的核心区，人口集中、经济发展十分活跃，是云南省经济和社会发展的核心区域，但水资源短缺，已经成为制约滇中地区经济发展的重要因素。

为了解决滇中缺水问题，进行了滇中引水工程项目。其中香炉山段，由于岩溶发育，地质条件复杂，目前有4 个线路方案，为了科学选定最佳方案，研究中利用上述的基于GIS 的层次分析法构建的综合评判优选栅格模型对该线路拟选出的4 个方案进行综合评判，为实际工程提供决策依据。

2.2 构建综合评价指标体系

对于确立的指标体系(见图1)，邀请专家对各因素的相对重要程度给予建议，综合分析各种情况后可构造目标层对于准则层U-P 因素的判断矩阵(见表2)，同理可求得各准则层对于指标层P-C 判断矩阵，见表3～表5，同时通过方根法计算相应权重并列于表中。

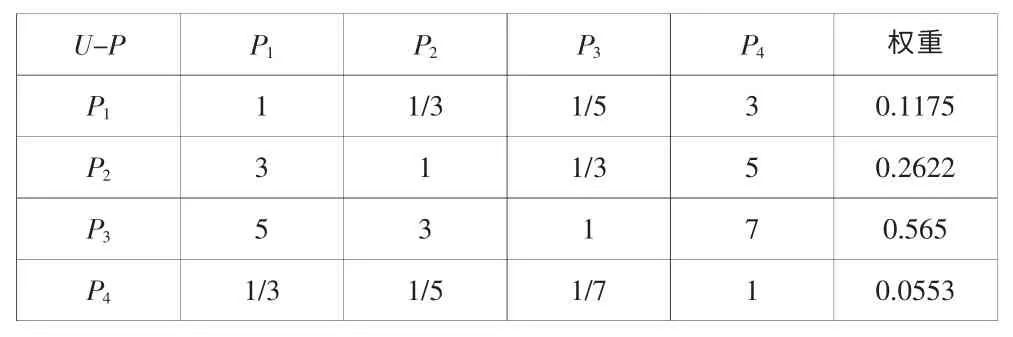
表2 U-P 判断矩阵Tab.2 Judgment matrix of U-P membership

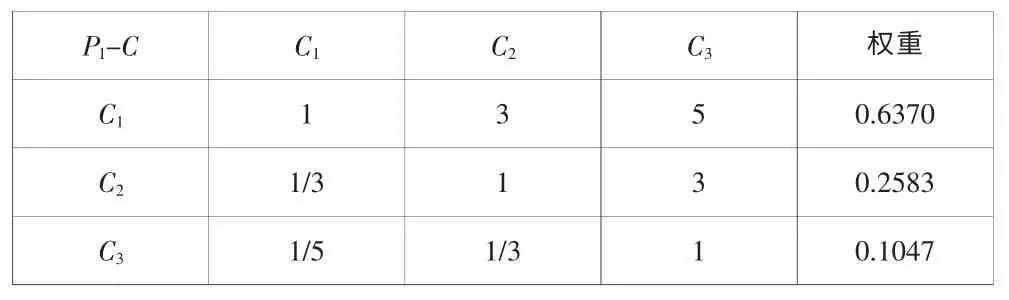
表3 P1-C 判断矩阵Tab.3 Judgment matrix of P1-C membership

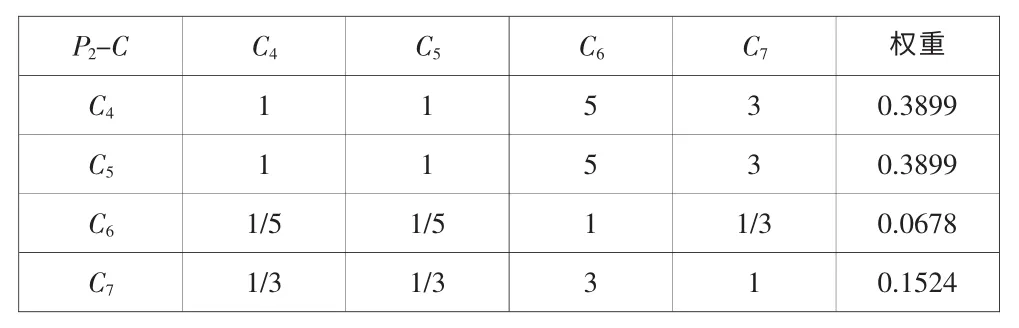
表4 P2-C 判断矩阵Tab.4 Judgment matrix of P2-C membership

表5 P3-C 判断矩阵Tab.5 Judgment matrix of P3-C membership

得出综合指标权重为C10.0748，C2为0.0304，C3为0.0123，C4为0.1022，C5为0.1022，C6为0.0178，C7为0.04，C8为0.0861，C9为0.2203，C10为0.2203，C11为0.0383，C12为0.0553。

2.3 综合评判优选栅格模型

根据选线评价因子的具体分析，在地形地貌、工程地质、水文地质和地震等数据重分类的基础上，结合层次分析法求得的权重值，进行叠加计算得到综合评判优选栅格模型，如图2 所示。

图2 综合评判优选栅格模型Fig.2 Comprehensive evaluation optimal grid model

2.4 确定最优方案

分别对香炉山隧洞线路方案Ⅰ、Ⅱ、Ⅲ、Ⅳ所穿过的栅格进行计算，得出各方案的评价指标值，如表7 所示。

中一线总分6420.5 分，平均值2.38；中二线总分6353.5 分，平均值2.36；中三线总分5882.9 分，平均值2.31；中四线总分6531.1 分，平均值2.31。

从以上的统计结果中可以看出，在综合考虑了费用总值和平均值的情况下，中三线的总费用和平均费用都是最小的，即本研究中的最优线路。

2.5 结论

（1）根据研究区域工程地质特点及生态环境特性，选取了11 个二级指标、4 个以及指标建立了长大引水线路方案综合评价指标体系，构造出研究区引水线路方案优选的评价与决策模型。

（2）基于GIS 技术，采用层次分析法（AHP），建立了一套快速对长大引水线路优选评价的方法。通过对影响因子的分析和评价，在GIS平台上把线路优选评价由定性评价实现了对线路优选评价的定量评价。

（3）本文根据云南省滇中引水工程线路选线特点进行相应优选评价研究，得出了中三线为最优线路，为实际工程建设提供了决策依据，对于类似特点的实际工程具有参考价值。

［1］鲍新华.比选法与层次分析法在农安支线供水线路优选中的应用[J].世界地质，2012，31(1):210-217.

［2］徐学军.模糊综合评价法在引江济巢工程引水线路优选中的应用[J].水资源与水工程学报，2011，22(3):138-141.

［3］卓宝熙，甄春相.遥感技术在铁路工程地质勘察中的应用[J].铁道工程学报，2005(S1).

［4］王明生，于金金.GIS 空间分析与铁路线路评价指标的量化[J].铁道勘察，2005(06).

［5］陈雪冬，杨武年.基于栅格数据道路选线模型算法的应用研究[J].公路，2004(05).

［6］陈守煜.系统模糊决策理论与应用[M].大连:大连理工大学出版社，1994.

［7］王新民，赵彬，张钦礼.基于层次分析和模糊数学的采矿方法选择[J].中南大学学报:自然版，2008，39(2):875.

［8］邓吉秋，鲍光淑.基于GIS 的层次分析法的应用[J].中南工业大学学报:自然科学版，2003，34(1):1-4.