基于议价博弈的卫星网络时隙分配算法

尹 译，梁 俊，肖 楠，王 轶，钟 贇

（空军工程大学 信息与导航学院，陕西 西安710077）

0 引 言

随着卫星通信技术的不断发展，业务传输QoS要求的提高与通信资源有限之间的矛盾日益突出，高效的卫星资源管理机制可以在满足用户传输需求的同时提高通信资源利用率，是卫星通信中需要解决的一个关键问题。资源管理问题的本质在于如何解决多个用户对通信资源的竞争，通过制定合理的资源分配方案，达到最优分配效能。作为解决竞争问题的典型理论，博弈论在资源调度领域被广泛应用［1］，通过建立相应模型有效地解决了某些资源竞争问题。文献 ［2］在协作博弈模型的基础上，提出分布式频谱的共享方法，解决了信道共享的问题；Niyato［3，4］在认知网络中定义多用户竞争主用户频段的效用函数，并基于此提出议价博弈的频谱价格问题；文献 ［5］对自私性CR 网络中的协作功率分配问题进行建模研究，通过求解纳什议价解，使节点间达到共赢的效果。文献 ［6］设计动态的二级博弈架构，实现了优化主次用户频率租借决策的目的。

目前博弈论应用研究主要关注功率和频率，对于时隙分配讨论较少。在MF－TDMA 卫星通信网络中，业务优先级差异引起的时隙分配公平性问题［7］是网络所面临的问题之一。针对该问题，本文引入博弈论观点，通过构建合理的收益模型，求解出系统最大收益点，并设计基于议价博弈的分配算法，在最大收益点的基础上获得理想的分配方案，提高业务间的公平性，改善低等级业务的服务质量。

1 卫星网络时隙分配问题

在MF－TDMA 卫星网络中，不同用户通过时隙分配的方式共享信道，如图1所示，由卫星根据时隙申请进行分配，用户利用时隙完成信息传输，实现多个用户对同一载波信道的共享。为保证通信质量，用户希望独享尽可能多的时隙，但受制于可分配时隙数目，用户获得的时隙有限，因此出现时隙的竞争行为。

图1 MF－TDMA 共享信道

根据业务QoS要求差异，ITU－T I.356标准将网络中业务分为恒定比特率CBR 业务、可变比特率VBR 业务、可用比特率ABR 业务、未定比特率UBR 业务，其中CBR、VBR、ABR 业务有严格的QoS要求，属于高等级业务，而UBR 业务则没有相关要求，属于低等级的尽力而为 （best efforts）业务。在具体时隙分配中，VBR 业务流速率可变且难以预测，系统为保证QoS，优先为其分配时隙资源，UBR 业务流则利用剩余时隙进行传输。这种分配的不公平严重损害了UBR 业务传输性能，特别是当VBR 业务流出现突发业务时，剩余时隙被过度占用，UBR 业务流缓冲队列增大，时延提高，某些情况下甚至造成阻塞。

上述时隙竞争的公平性问题可抽象为博弈参与者利益分配问题，通过借鉴议价博弈模型中出价—妥协—出价机制解决，使业务间做出合理让步，最终形成各业务均能接受的时隙分配方案，这是本文的出发点。

作为一种典型合作性博弈，议价博弈［7］假设参与者们虽存在利益冲突，但可以通过相互协商达成互惠的结果。议价博弈的进程可被描述为：

（1）议价周期开始，竞拍者A 向竞拍者B 提出利益分配方案。

（2）若B接受，议价周期结束，分配方案形成。若B不接受，向A 提出新的分配方案。

（3）若A 接受，议价周期结束，分配方案形成。若A不接受，开始新的议价周期。

根据无名氏定理 （folk theorem）［8］可以证明，在数轮的议价之后，最终的定价方案带来的收益能够达到A、B理性条件［9］下可行收益。

2 基于议价博弈的模型建立

2.1 网络模型

假设用户和卫星之间的往返时延为τ，用户 （假定每个用户只传输单类型的业务流）在t 时刻获得的时隙数n（t）实际是卫星对t－τ时刻发送的时隙请求n（t－τ）的响应，这种固有长时延τ的存在使用户与卫星间无法频繁交互博弈信息，不能满足议价博弈对于完全信息［10］的要求，故需在星上为用户配置代理，代替用户进行博弈，如图2所示。

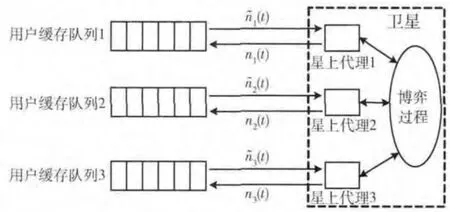
图2 博弈代理的设置

业务的缓存队列长度是星上代理在博弈中选择行为的依据，能反映业务到达的速率以及拥塞状态。由于星地交互时延，用户不能实时向卫星告知队列长度L（t），只能由星上代理根据已掌握信息完成有关队列状态的推断。下面介绍一种适用于星上代理的地面缓存队列状态的估计方法。

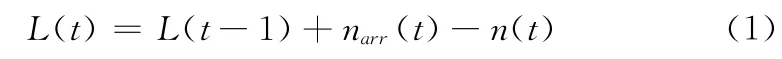
式中：narr（t）——t时刻到达队列的待发送信元数。

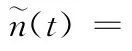
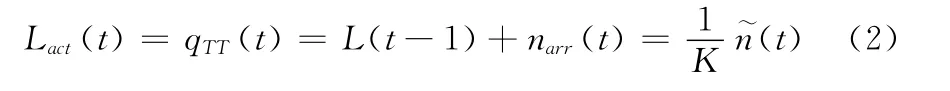
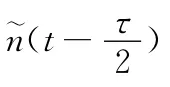
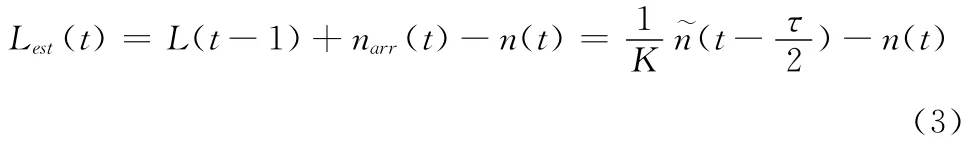
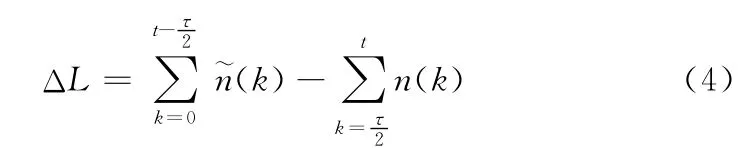
队列增量ΔL从时隙的需求和分配角度估计地面缓存队列的状态，若ΔL 较大，表明队列长度增加，用户时延增大，可能出现拥塞；若ΔL 较小，表明用户缓存队列空闲，可以适当为其他用户提供时隙。在博弈过程中，代理根据ΔL 值决定可妥协程度，使议价完全基于传输需求，避免业务类型差异带来不公平。

2.2 收益模型

博弈论定义收益是指参与者通过执行策略所获得的利润。本文中系统获得的收益包括：①经济收益，即系统为用户提供传输服务需收取一定的利润；②社会影响，指用户给予系统正面或负面的评价及在行业内产生的连锁效应。同理，用户在使用卫星实现业务传输时，也会为其自身带来相应的经济收益和社会影响。

卫星通信系统中，用户通过向系统申请时隙实现其数据传输，在这个过程中，卫星系统和用户都需要考虑各自收益。为了达到系统收益最大化，设其收益是关于为不同用户i分配时隙数ni的函数，构造以下系统收益函数

式中：c——待定变量，表示卫星 “出售”单位时隙的成本，包含系统损耗、功率开销等方面；pi——用户i “购买”单位时隙所支付给系统的价格。时隙价格一方面与用户需求满足程度相关，另一方面受到用户间的公平性影响，故时隙价格是关于分配时隙数ni的函数pi（ni）。

在经济学中，量化偏好间的相对关系采用序数效用，其描述模式［13］有完全替代模式、完全互补模式、准线性偏好模式、柯布—道格拉斯偏好模式。由于需求满足程度和用户公平性处于可相互替代关系，故按照完全替代模式构造单位时隙价格函数

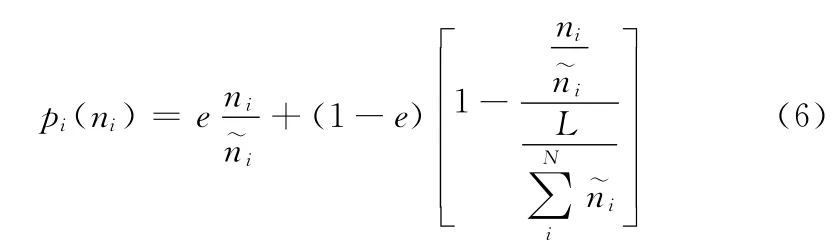
衡量用户间的公平性。

当用户获得n 个时隙进行业务传输，带来相应收益，而付出的代价是时延对于业务质量的影响。定义用户收益函数

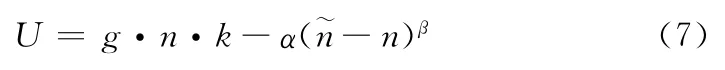
2.3 最佳收益点

在2.2节建立的系统收益模型中，卫星可以通过调节用户分配时隙数来获得最佳收益。为了便于研究系统最佳收益点及相应条件，假定参加时隙分配只有2个用户，令U′SS（n1，n2）＝0 可解得系统收益最大的时隙分配方案

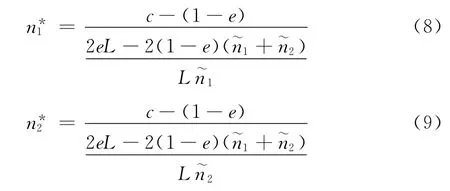
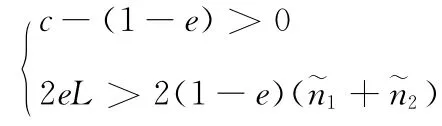
解得

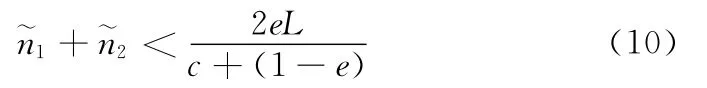
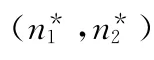
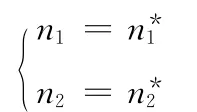
条件 （10）不成立时，（n1，n2）＝（n）无法在约束条件n1＋n2≤L 下取得，用户间形成时隙竞争，由星上代理代替用户进行议价，最终形成双方接受的分配方案。

3 时隙分配算法

当卫星不能提供（nA，nB）＝（n）的分配方案时，由用户的星上代理进行时隙竞争，通过博弈最终产生令双方都接受的时隙的分配方案。用户议价博弈过程可以用图3中算法框架描述。

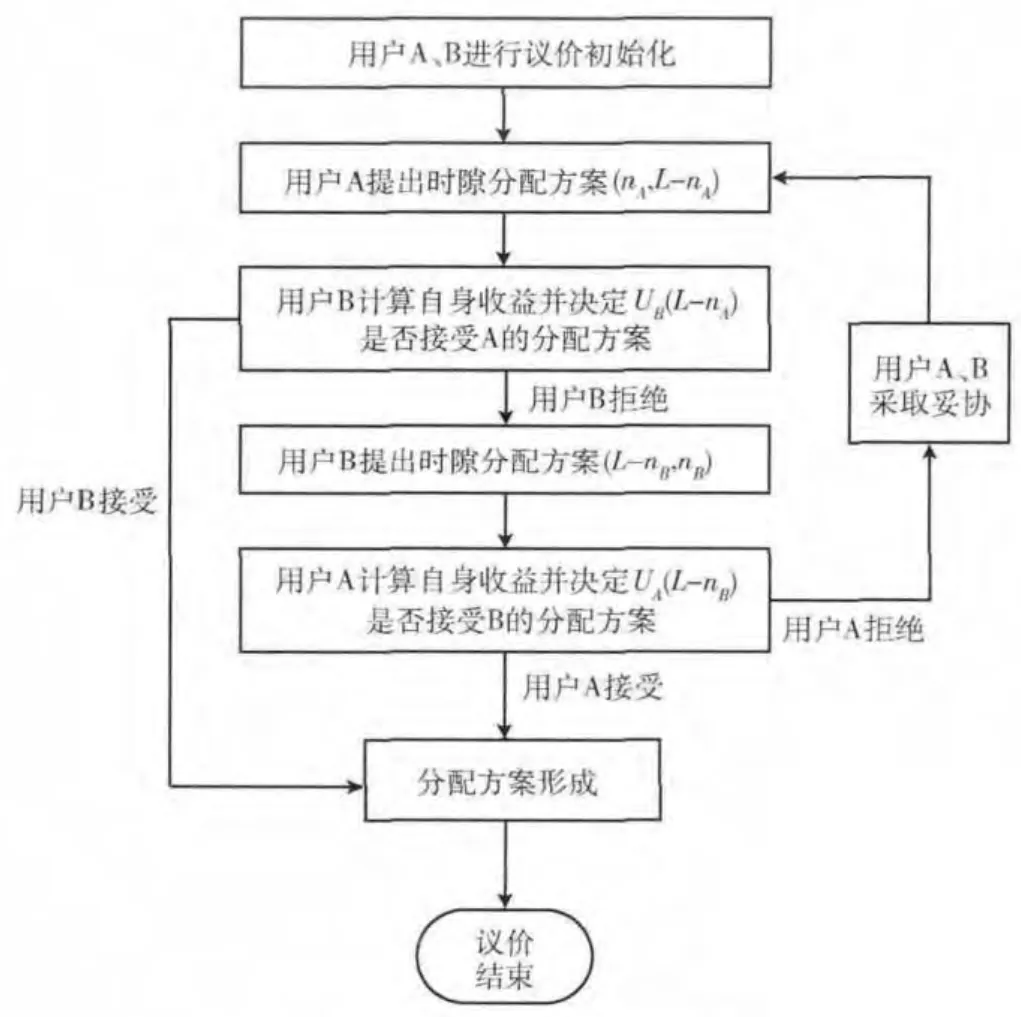
图3 议价博弈过程的算法

由于卫星处理分配的时间有限，数个失败的议价周期会导致待分配的时隙无法被利用，系统和用户均不能获得收益。所以在单个不成功的议价周期后，用户再次提出的分配方案时应进行某种程度的 “妥协”。描述妥协可引入博弈论中贴现因子δ（0＜δ＜1），根据文献 ［7］的解释，δ体现博弈参与人的耐心程度，其值越大说明议价的耐心越大，做出的妥协越小。用户A 在第k＋1次出价为

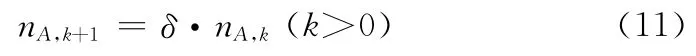
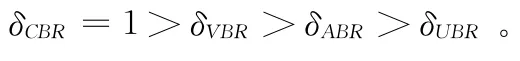
在决定是否接受A 所提分配方案时，用户代理由式（4）、式 （9）计算分配方案（nA，k＋1，L－nA，k＋1）对应的收益（UA，UB），将UB与B所期望收益U′B比较，有

4 仿真及结果分析

与传统分配算法优先保证高等级业务流所不同，本文所提时隙分配算法侧重于提升业务间的公平性，从而改善低等级业务的服务质量。为了验证该算法在系统中的性能，设置时隙获得数与请求数的比值和缓存队列长度2个指标，前者衡量时隙分配的公平性，后者反映业务的发送速率及拥塞程度，构建如下仿真环境：

用户A、B在MF－TDMA 卫星网络中利用某信道进行传输服务，其中A 以VBR 方式发送一段MPEG－4格式视频，每帧大小分布如图4所示；B以UBR 方式进行文件数据上传，限定上传峰值速率不超过1 Mbps。

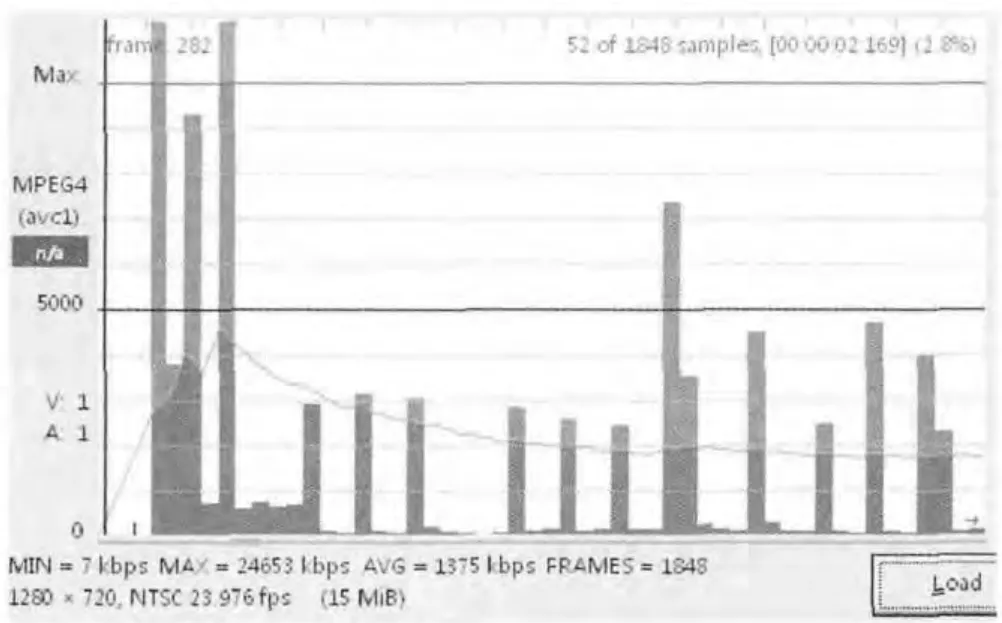
图4 视频帧大小分布

每帧中可供分配时隙总数L＝30，帧长40ms，信道最大速率3 Mbps。约定A、B的议价博弈贴现因子

由式 （4）可知，在n＜n 时，收益U 是分配时隙数n的单调增函数，故仿真中采用n 等价代替U。设定用户接受议价的收益条件

仿真通过上述信道传输用户A、B 数据，时隙分配采用基于议价博弈的分配算法；同时在另一相同系统中采用加权轮询 （weighted round robin）的分配方式，作为对照组进行实验。仿真结果如图5～图7所示。

图5 UBR 业务时隙供需比nB／n～B

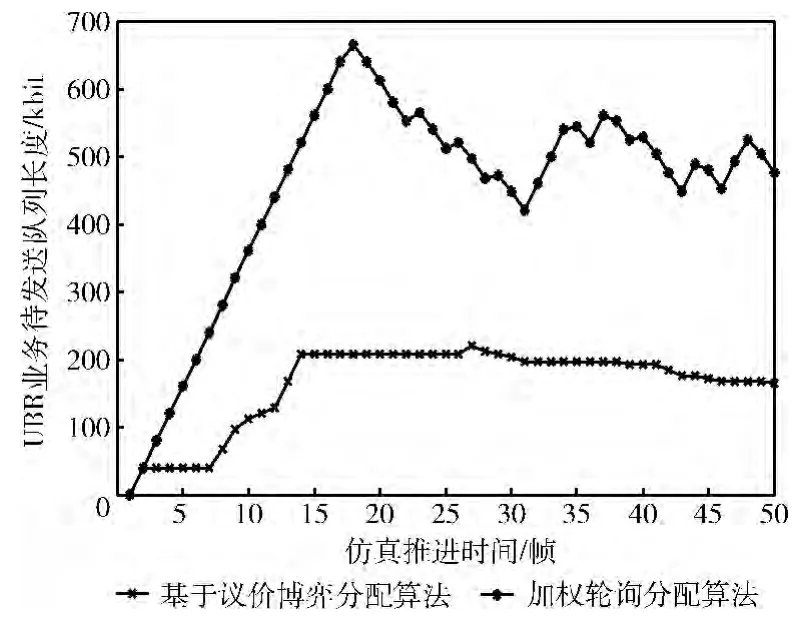
图6 UBR 业务缓冲区队列长度

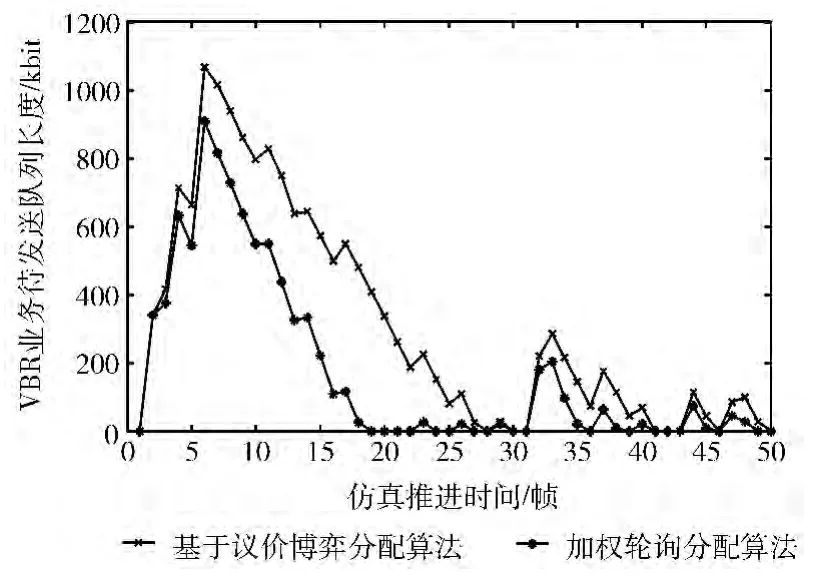
图7 VBR 业务缓冲区队列长度

由图5可知，加权轮询分配算法不能有效满足UBR 业务的时隙请求，特别是当用户A 出现突发业务时 （1～16帧），VBR 业务占据所有时隙，UBR 业务传输停滞，极大损害了业务间公平性。而基于议价博弈的时隙分配算法的值集中在1附近，即使出现VBR 突发业务，只造成短暂下降，不会中断UBR 业务传输，使UBR 业务获得较好的传输性能。这是因为加权轮询分配算法优先满足高权重VBR 业务流的时隙请求，低权重UBR 业务流只能使用部分剩余时隙，无法获得可靠的传输性能保证；而在基于议价博弈的时隙分配算法中，分配依据是传输需求而不是业务优先级，确保时隙分配给最需要的业务流，避免高等级业务在轻负载下过度占用时隙，改善了业务间的公平性。

图6、图7分别是2种分配算法下UBR、VBR 业务的缓冲区队列长度。从图6可以看出，基于议价博弈的分配算法能有效减少UBR 业务缓冲区队列长度和拥塞概率，提高传输速率，避免突发VBR 业务造成传输速率波动，改善用户的服务质量。在图7中，基于议价博弈的分配算法缓冲区队列长度变化趋势与加权轮询分配算法相同，表明其传输速率仍能根据业务的到达速率进行调整，对突发业务拥有良好的适应性。但是，VBR 业务传输性能出现部分下降，这是由于在议价过程中用户A 存在 “妥协”行为，减少了对时隙的需求。

5 结束语

针对MF－TDMA 卫星时隙分配公平性问题，本文从博弈论的观点出发，构建相应的网络结构和收益模型，并讨论系统最大收益的存在性问题，最终提出一种基于议价博弈的时隙分配算法。在该算法中，业务流之间在最大受益点的基础上，依据实际需求进行议价博弈，通过合理妥协退让，形成理想的分配方案。为使卫星能够克服长时延估计业务缓冲区队列状态，还设计了相应的队列长度估计方法。算法虽然没有明确考虑业务类型的优先级，但却将优先级包含在议价得可妥协程度中，不违背ITU 所提倡的业务分类原则。仿真结果表明，该算法以高等级业务性能部分下降为代价，有效提升业务间公平性，大幅改善低等级业务的服务质量。但是，本文仅讨论了算法在包含2个用户的系统中的性能，对于多用户系统的研究有待于以后完善。

［1］XU Li.Applications of game theory in wireless communication network ［M］.Beijing：Science Press，2012 （in Chinese）.［许力.博弈理论在无线网络中的应用 ［M］.北京：科学出版社，2012.］

［2］Suris JE.Cooperative game theory for distributed spectrum sharing ［C］／／IEEE International Conference on Communications，2007：5282－5287.

［3］Niyato D，Hossain E.Competitive spectrum sharing in cognitive radio networks：A dynamic game approach ［J］.IEEE Transactions on Wireless Communications，2008，7 （7）：88－94.

［4］Niyato D，Hossain E.Competitive pricing for spectrum sharing in cognitive radio networks：Dynamic game，inefficiency of nash equilibrium，and collusion ［J］.IEEE Journal on Selected Areas of Communications，2008，26 （1）：192－202.

［5］LIU Peng.Performance improvement algorithms based on bar－gaining game theory for wireless cooperative relay networks［J］.Telecommunication Engineering，2012，52 （5）：770－775（in Chinese）.［刘鹏.基于议价博弈论的无线协作中继网络性能改进算法 ［J］.电讯技术，2012，52 （5）：770－775.］

［6］Zhu Kun，Niyato D.Dynamic spectrum leasing and service selection in spectrum secondary market of cognitive radio networks［J］.IEEE Transactions on Wireless Communication，2012，11 （3）：1136－1145.

［7］ZHANG Weiying.Game theory and information economics［M］.Shanghai：Shanghai People’s Publishing House，2012（in Chinese）. ［张维迎.博弈论与信息经济学 ［M］.上海：上海人民出版社，2012.］

［8］Le Treust M，Lasaulce S.A repeated game formulation of energy－efficient decentralized power control ［J］.IEEE Transactions on Wireless Communications，2010，9 （9）：2860－2869.

［9］JIANG Junli.Logic study of epistemic and rational conditions of some game－theoretic solutions［J］.Computer Science，2010，37（5）：223－227（in Chinese）.［蒋军利.对博弈解概念认知和理性条件的逻辑分析［J］.计算机科学，2010，37 （5）：223－227.］

［10］Aumann RJ.Backward induction in games of perfect informa－tion ［C］／／27th Annual ACM／IEEE Symposium on Logic in Computer Science，2012：1－2.

［11］Vassaki S，Panagopoulos AD，Constantinous Philip，et al.Market－based bandwidth allocation for broadband satellite communication networks ［C］／／Second Conference on Advances in Satellite and Space Communications，2010：110－115.

［12］QIN Yong.MAC protocol based on bandwidth on demand（BoD）in DVB－RCS satellite communication systems ［J］.Journal of Astronautics，2010，31 （3）：838－843 （in Chinese）. ［秦勇.基于带宽按需分配的DVB－RCS 宽带卫星MAC协议 ［J］.宇航学报，2010，31 （3）：838－843.］

［13］LI Wenbian.A microeconomics based dynamic spectrum management algorithm for cognitive wireless networks ［J］.Journal of Electronics ＆Information Technology，2009，31（4）：897－902 （in Chinese）.［黎文边.认知无线网络中基于微观经济学的动态频谱管理算法 ［J］.电子与信息学报，2009，31 （4）：897－902.］

［14］Simeon O，Gunduz D，Poor HV，et al.Compound multipleaccess channels with partial cooperation ［J］.IEEE Transactions on Information Theory，2009，55 （6）：2425－2441.