模糊系统建模方法及其在微生物发酵中的应用

周 頔，孙 俊

（1.江南大学 数字媒体学院，江苏 无锡214122；2.江南大学 物联网工程学院，江苏 无锡214122）

0 引 言

在实际的微生物发酵工程中，经常需要根据现有的发酵结果来预测其它不同实验条件下相关微生物的产量。从节约成本的角度来说，最理想的方法应该是通过建立该种微生物发酵的模型来仿真整个发酵的过程，而不是通过不断投入人力、物力、时间做真实的测试实验。因为微生物发酵过程往往需要例如时间、温度、Ph值、以及多种反应物的共同参与，也就是说建立起来的应该是一种具有多输入变量的发酵模型。而输入变量数量越多，对模型建立提出的难度要求就越高。

自适应模糊推理系统 （ANFIS）［1］，是结合了模糊控制与神经网络形成的一种智能控制方法。这种方法基于T－S模糊模型［2，3］而建，用神经网络模拟并求解模糊系统中的模糊化、模糊推理和反模糊化3 个基本过程。因此，ANFIS实际是用神经网络的方法来完成模糊系统的功能。正因为ANFIS这样的特点，使之既可以利用神经网络的学习机制自动从输入输出数据中提取规则，又可以兼具有模糊系统清晰的语言表达能力。

为了进一步提高ANFIS建模的精度，并使之能应用到微生物发酵仿真中，本文将混合聚类算法与具有量子行为的粒子群算法引入传统的ANFIS 建模过程中：在ANFIS系统的前件参数识别部分，采用混合型模糊聚类算法对输入空间进行划分，每个聚类分布都拟合为高斯函数，从而可以得到对应的初始隶属度函数参数；通过具有量子行为的粒子群算法与最小二乘法相结合的策略迭代求解并优化整个ANFIS的前件及后件参数，直至获得符合精度要求的模糊系统模型。采用混合聚类算法的目的在于克服各种单一聚类算法［4－7］中需要事前指定聚类数目、聚类效果依赖聚类中心初始值等缺点。

1 核心算法

1.1 ANFIS

传统的具有式 （1）、式 （2）两条模糊规则的ANFIS，由图1可见，其结构共分五层。

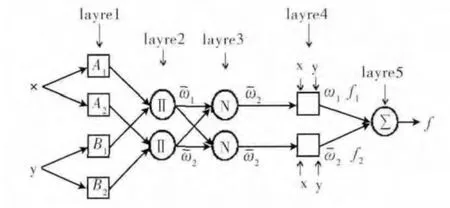
图1 ANFIS结构

第一层：隶属度函数层。该层的输入x，y 为精确输入值，输出O1为隶属度

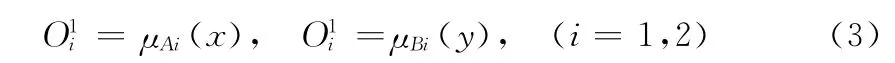
三角函数、高斯函数等往往是这一层中隶属度函数的较好选择。这些函数中的参数 （例如高斯函数中的c和σ）即被称为ANFIS的前件参数θ1

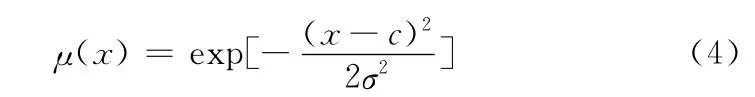
第二层：规则的权重计算层。该层输入为隶属度，输出O2为隶属度的乘积

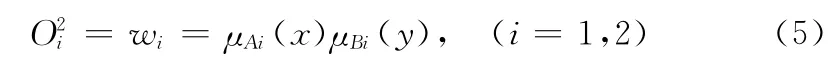
第三层：规则的权重归一化层

第四层：模糊规则输出层。该层输入为第一层中的输入x，y，和第三层中的归一化权重

wi，输出为每条模糊规则的加权结果O4

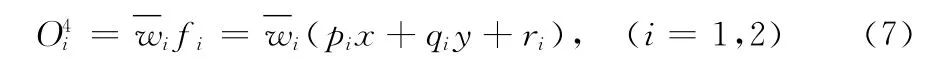
这一层中的参数 ｛qi，pi，ri，｝ （i＝1，2）即被称为ANFIS的后件参数θ2。

第五层：系统输出层。该层是一个求和操作，输出O5为精确值

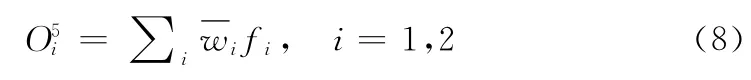
因此，整个ANFIS系统建模的过程就是识别θ1和θ2的过程。通常来说，假设前件参数已确定为θ′1，式 （7）也可重写为后件参数θ2的函数

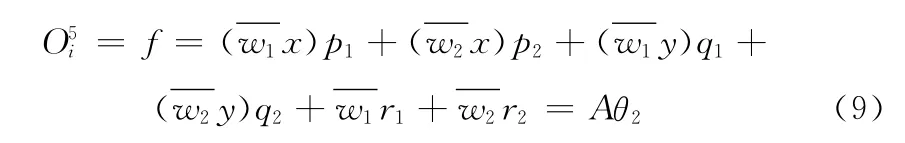
此时若有一定规模的系统输入输出值，就可以很容易地根据最小二乘法得到系统后件参数θ2的最佳估计值θ′2

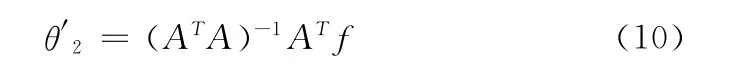
那么建立起来的ANFIS系统的实际输出为

则对于一个输入数据数目为n 的ANFIS系统来说，其实际输出与目标输出之间的差距可用均方根差E 来衡量

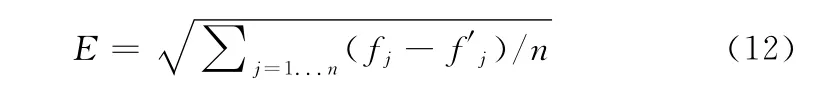
因此，ANFIS建模过程往往就是通过不断尝试确定前件参数θ2，并用最小二乘法确定此时的后件参数θ2，以及系统的均方根差E，然后通过调整θ1达到不断降低E 直至E 达到一定容错范围之内的过程。

1.2 具有量子行为的粒子群算法QPSO

QPSO 算 法［8，9］是 一 种 将 传 统 粒 子 群 算 法PSO 的 发 生环境转移到量子空间中，从而使每个粒子的行为都符合量子动力学的高性能粒子群类优化算法。QPSO 算法由波函数来描述粒子位置，并由薛定谔方程来决定粒子的状态变化。每个粒子的位置迭代更新方程为

其中u～U（0，1），mbest为所有个体最优位置的平均值，对于D 维空间来说，即

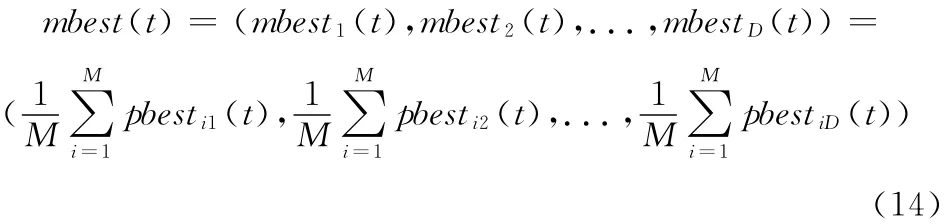
而qi则为局部吸引子

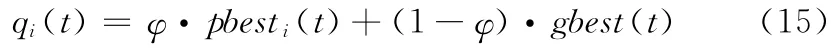
其中gbest为所有粒子的当前全局最优位置，φ ～U（0，1）。因此β是QPSO 算法中唯一的参数，被称为收缩扩张因子，用来控制整个算法的收敛速度。文献 ［10］证明，当β＜1.782时，算法可保证收敛。因为QPSO 算法通过借鉴群体中所有粒子的位置建立了分布概率模型，然后通过随机采样完成对群体的更新，所以QPSO 的算法性能大大优于PSO 算 法及很多遗 传算法［11，12］。

1.3 混合聚类算法

为解决传统模糊聚类算法FCM 中聚类数目需要事先指定、算法性能强烈依赖与初始聚类中心、聚类过程容易陷入局部最优值等缺陷，本文将减法聚类的思想融入传统FCM 算法中，将减法聚类算法确定出初始聚类个数和初始的聚类中心，作为初始值代入FCM 算法最终得到精确的聚类中心。这样做，使提出的混合聚类算法既不要事先指定聚类数目及聚类中心，又具有较高的聚类精度。

提出的混合聚类算法以下述式 （16）为目标函数，模糊聚类的过程就是最小化Jm的过程

具体的混合聚类算法步骤流程如图2所示。

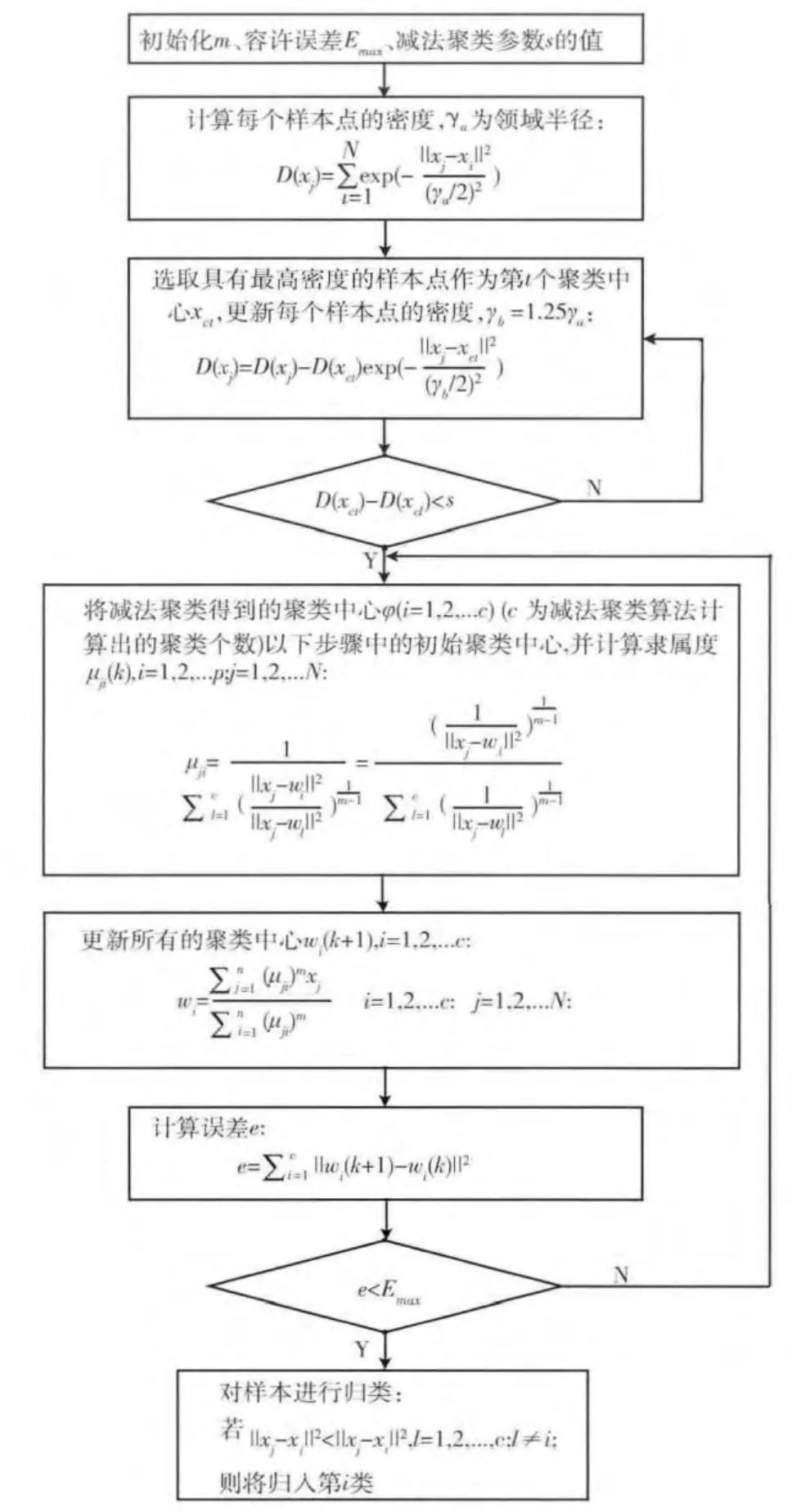
图2 混合聚类算法流程

2 具有量子行为模糊系统建模方法HQB－ANFIS

为了避免网格划分输入空间造成的维数灾难问题，也同时为了减少整个ANFIS 模糊系统建模过程中的人工干预、并提高精度，本文提出一种融合混合聚类和QPSO 算法的新型ANFIS 模糊系统建模方法 （hybrid quantum behaved－ANFIS，HQB－ANFIS）：采用1.3节中提出的混合聚类算法对输入空间进行自动划分，每一个聚类通过高斯函数的拟合产生一个隶属度函数，即完成ANFIS系统的前件参数——隶属度函数参数的初始识别，然后通过QPSO 算法与最小二乘法优化前件参数，直至达到停机条件，最终得到ANFIS的前件及后件参数。

用QPSO 实现ANFIS系统的参数识别过程中，每个粒子的维数即为ANFIS系统前件参数的个数，每一维都代表了ANFIS的一个前件参数，式 （12）即为整个算法的目标函数。

基于QPSO 算法的ANFIS参数优化流程如下所示：

步骤1 初始化：粒子维数等于前件参数的个数，第i个粒子的位置设为Xi（t），迭代计数t＝1；

步骤2 对每一个粒子，根据式 （3）～式 （5）计算所有规则的权重wj和归一化权重，（1＜＝j＜＝l，l为规则数），并由式 （9）根据输入数据集和得出系数矩阵A；再由式 （10）计算出后件参数的最佳估计值θ′2；最后由式 （11）、式 （12）计算出此时ANFIS 的均方根差E，作为该粒子的当前目标函数值f（Xi（t））；

步骤3 根据式 （14）计算粒子群的平均最优位置；

步骤4 判断是否更新粒子的个体最优位置Pi（t）：若f ［Xi（t）］＜f ［Pi（t－1）］，则Pi（t）＝Xi（t）；否则Pi（t）＝Pi（t－1）；

步骤5 计算群体当前的全局最优位置Pg（t），g＝min｛f ［Pi（t）］｝；

步骤6 判断是否更新群体的全局最优位置Pg（t）：若f ［Pg（t）］＜f ［Pi（t－1）］，则Pg（t）＝Pg（t）；否则Pg（t）＝Pg（t－1）；

步骤7 根据式 （12）的进化公式计算粒子新的位置；

步骤8 重复步骤2～步骤7，直至达到一定的循环结束条件。

3 实 验

为了验证本文提出的HQB－ANFIS算法的有效性，将算法应用到时间序列的预测问题、以及抗坏血酸2－葡萄糖苷 （AA－2G）的发酵生产模型预测中，与传统的基于标准网格划分的BP－ANFIS、基于网格划分和粒子群优化算法改进的ANFIS （PSO－ANFIS）、以及这2 种算法在本文提出的混合聚类方法下的算法HBP－ANFIS、HPSO－ANFIS，还有采用标准网格划分的QB－ANFIS算法进行对比实验。在所有实验中，QPSO 和PSO 中的粒子群个数均为50，QPSO 算法的α值从1递减到0.5，PSO 算法中的参数ω＝0.7，c1＝1.5，c2＝1.5。所有算法中的迭代次数均取为2000次。所有实验中的隶属度函数均定为高斯函数。

3.1 Machey－Glass混沌时间序列预测

Machey－Glass时间序列由如下差分延迟方程产生

需要用时间序列中t时刻前的值来预测未来t＋p 内点的值。为了获得每一个时间点的序列值，可用四阶龙格－库塔法求解，初始条件为x （0）＝1.2，τ＝1.7。按如下格式抽取1000个点作为系统的输入数据： ［x（t－18），x（t－12），x（t－6），x（t）；x（t＋6）］。其中118≤t≤1117。前500组数据用于训练，后500组用于测试。与非线性系统建模实验，三组采用混合聚类的实验中，判断减法聚类是否停止的参数s均取为0.5，得到的聚类个数为10类。其它使用网格划分的实验中，对每个变量均取2 个隶属度函数，即该系统有16条模糊规则。

对比实验结果见表1，RMSEtrn为训练均方误差，RMSEchk为检测均方根。从表1中可见，所有采用了混合聚类方法的算法都在只需要10条模糊规则的前提下，比对应的需要16条模糊规则的采用了标准网格划分方法的算法能达到更高的精度。说明混合聚类算法对输入变量较多的模糊系统识别十分有效。图3为系统在x （124）～x （1124）的实际输出与模糊系统在HQB－ANFIS算法下的输出，从图可见，两者基本完全吻合。

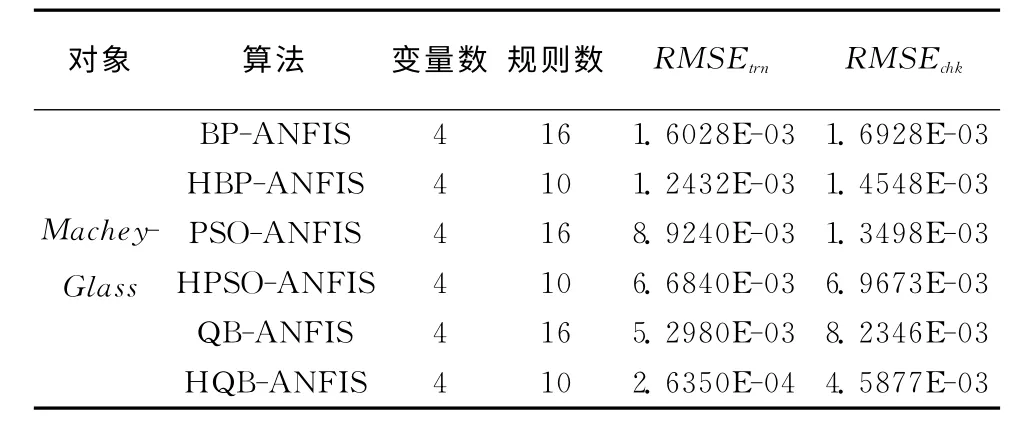
表1 Machey－Glass时序预测实验结果

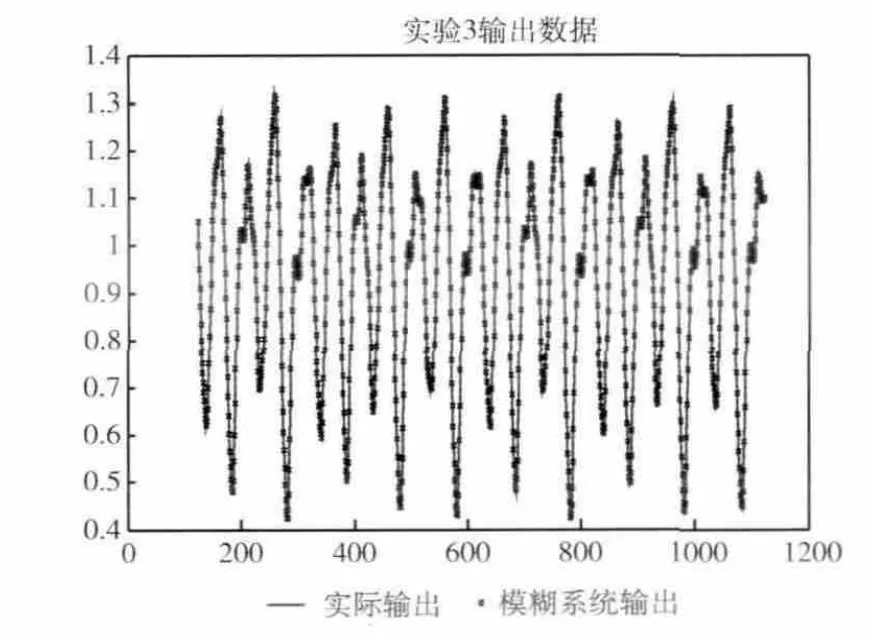
图3 Machey－Glass时序预测实验的实际输出与HQB－ANFIS方法下的系统输出对比

3.2 抗坏血酸2－葡萄糖苷生产发酵模型中的应用

将提出的HQB－ANFIS模糊系统建模方法应用到抗坏血酸2－葡萄糖苷 （AA－2G）的发酵生产模型预测中。抗坏血酸2－葡萄糖苷的产量与5个关键的输入变量有关：时间、温度、pH 值、vc浓度、环糊精浓度。表一是实际发酵过程中，50次不同实验输入变量下AA－2G 的产量，可以看到当这5个输入变量中的任何一个有微小不同时也会影响最终的AA－2G 产量。

根据表2 中的50 组数据，分别采用HBP－ANFIS、HPSO－ANFIS和HQB－ANFIS建立抗坏血酸2－葡萄糖苷的生产模型。将反应的时间、温度、pH 值、vc浓度、环糊精浓度这5个变量定为系统的输入：x1、x2、x3、x4、x5，并将AA－2G的产量定为y。HQB－ANFIS中混合聚类算法步骤中参数s的取值为0.5，产生了15个聚类，根据一个聚类产生一条模糊规则的系统辨识方法，即可得到模糊系统的15条模糊规则。所有算法迭代次数均为2000 次。所有实验中的隶属度函数均定为高斯函数。

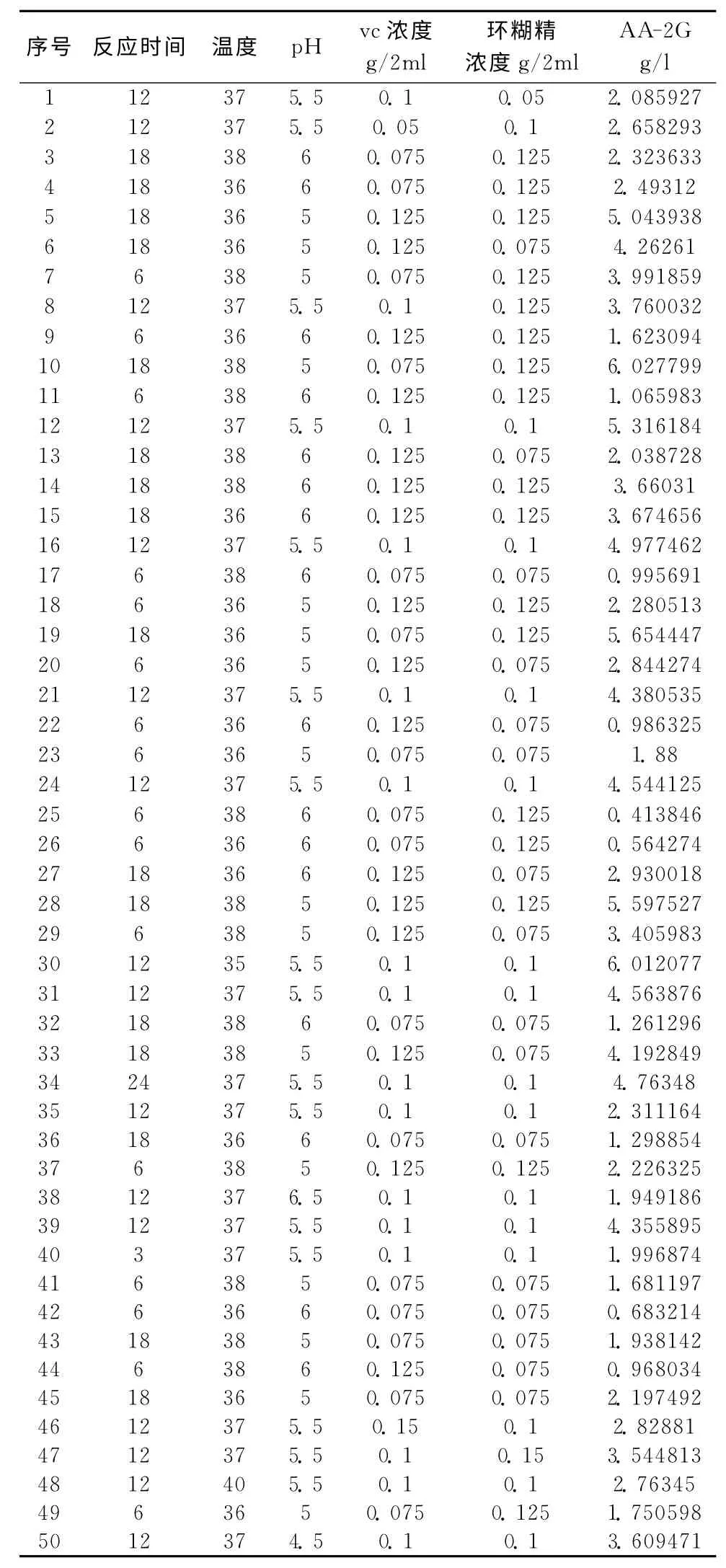
表2 50组实际试验的AA－2G 产量数据

3种算法建立出的模糊系统的输出预测值、以及与真实值之间的误差列于表3中，（－＊代表－ANFIS，例如：HBP－＊即表示HBP－ANFIS）。可以明显看出HQB－ANFIS模糊系统的精确度最高，误差最小。图4为HQB－ANFIS模糊系统对这50组数据的输出误差。从图4 （a）以及图4 （b）中均可看出，除了对序号为12、16、24、31、35这5个样本的预测误差较大外，其余45个样本的误差均在10－4左右，对实际工业微生物发酵生产中，完全可以忽略不计。

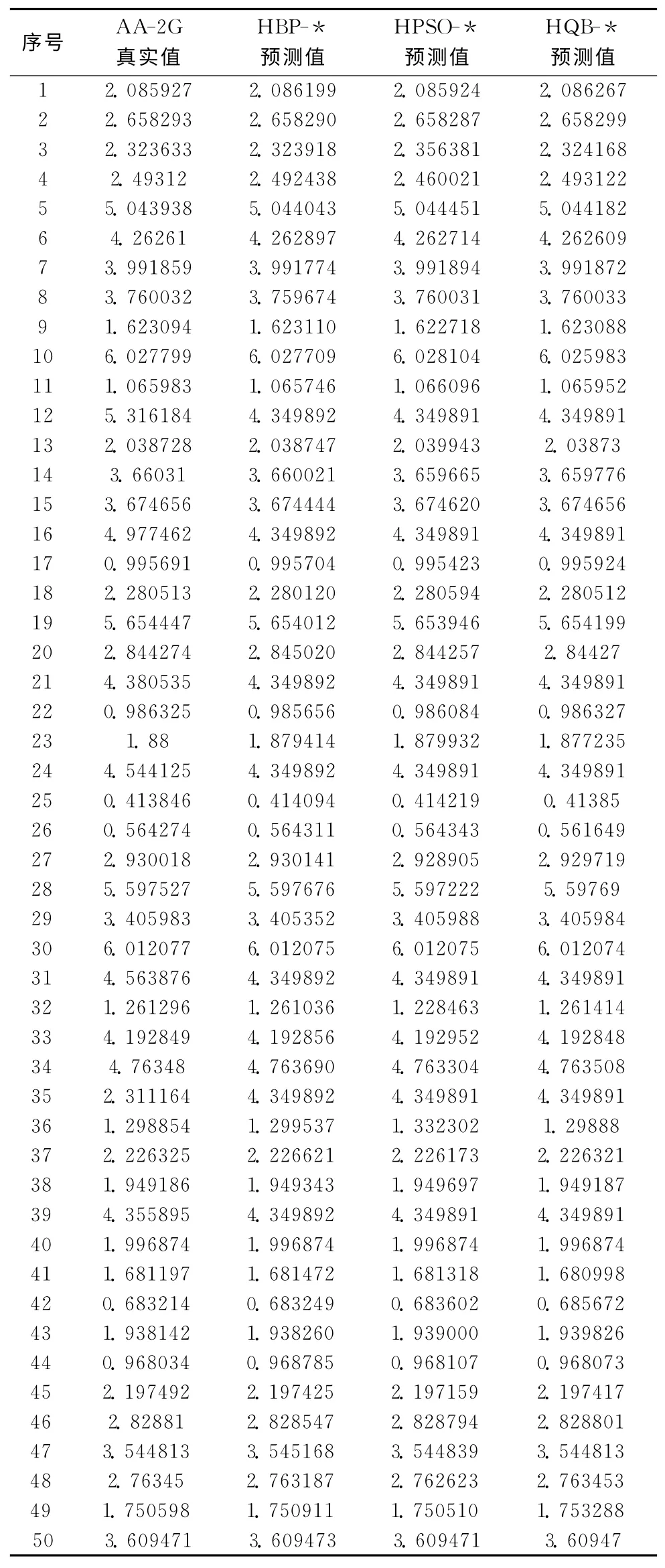
表3 3种对比算法得出的产量预测值及误差

图4 HQB－ANFIS模糊系统输出误差

4 结束语

本文提出了HQB－ANFIS算法，采用一种混合型模糊聚类算法来对模糊系统的输入空间进行划分，每一个聚类通过高斯函数的拟合产生一个隶属度函数，即完成ANFIS系统的前件参数——隶属度函数参数的初始识别，然后通过具有量子行为的粒子群算法QPSO 与最小二乘法优化前件参数，直至达到停机条件，最终得到ANFIS的前件及后件参数，从而得到满意的模糊系统模型。并将HQB－ANFIS算法应用到实际微生物发酵模型的建立中，通过50组实验数据的对比表明，提出的HQB－ANFIS与传统的基于BP算法或PSO 算法的ANFIS模型建立方法相比，具有更高的精确度，达到了实际应用的需求。

［1］Rajesh Singh，Ashutosh Kainthola，Singh TN.Estimation of elastic constant of rocks using an ANFIS approach ［J］.Applied Soft Computting，2012，12 （1）：40－45.

［2］Ahmad Kalhor，Babak N Araabi，Caro Lucas.A new systematic design for habitually linear evolving TS fuzzy model［J］.Expert Systems with Applications，2012，39 （2）：1725－1736.

［3］Raad Z Homod，Khairul Salleh Mohamed Sahari，Haider AF Almurib，et al.RLF and TS fuzzy model identification of indoor thermal comfort based on PMV／PPD ［J］.Building and Environment，2012，49：141－153.

［4］Mark Polczynski， Michael Polczynski.Using the k－Means clustering algorithm to classify features for choropleth maps［J］.The International Journal for Geographic Information and Geovisualization，2014，49 （1）：69－75.

［5］Krinidis S，Chatzis V.A robust fuzzy local information CMeans clustering algorithm ［J］.IEEE Transactions on Image Processing，2010，19 （5）：1328－1337.

［6］Tamalika Chaira.A novel intuitionistic fuzzy C means clustering algorithm and its application to medical images ［J］.Applied Soft Computing，2011，11 （2）：1711－1717.

［7］Cao Hongbao，Deng Hong－Wen，Wang Yu－Ping.Segmentation of M－FISH images for improved classification of chromosomes with an adaptive fuzzy c－means clustering algorithm ［J］.IEEE Transactions on Fuzzy Systems，2012，20 （1）：1－8.

［8］Sun Jun，Fang Wei，Wu Xiaojun，et al.Quantum－behaved particle swarm optimization：Analysis of individual particle behavior and parameter selection ［J］.Evolutionary Computation，2012，20 （3）：349－393.

［9］Sun Jun，Fang Wei，Vasile Palade，et al.Quantum－behaved particle swarm optimization with Gaussian distributed local attractor point ［J］.Applied Mathematics and Computation，2011，218 （7）：3763－3775.

［10］Sun J，Xu W－B，Feng B.Adaptive parameter control for quantum－behave particle swarm optimization on individual level［C］／／Proc of IEEE Int Conf on Systems，Man and Cybernetics.Hawaii：IEEE Press，2005：3049－3054.

［11］ZHOU Di，SUN Jun，XU Wenbo.Quantum－behaved particle swarm optimization algorithm with cooperative approach ［J］.Control and Decision，2011，26 （4）：582－586 （in Chinese）.［周頔，孙俊，须文波.具有量子行为的协同粒子群优化算法 ［J］.控制与决策，2011，26 （4）：582－586.］

［12］Sun J，Wu X，Palade V，et al.Convergence analysis and improvements of quantum－behaved particle swarm optimization［J］.Information Sciences，193，2012：81－103.