脑电数据近似熵与样本熵特征对比研究

李 立，曹 锐，相 洁，2＋

（1.太原理工大学 计算机科学与技术学院，山西 太原030024；2.北京工业大学 国际WIC研究院，北京100000）

0 引 言

脑电（electro encephalo gram，EEG）是一种非常复杂的非线性信号，近几年来非线性的方法已经开始广泛应用于脑电信号的分析中。非线性指标 （如熵）可以很好地揭示大脑的混沌行为［1］。而近似熵（approximate entropy，ApEn）和样本熵（sample entropy，SampEn）是量化时间序列复杂性和研究时间序列性质的重要工具，并被广泛应用于很多研究领域，特别是生物医学信号的研究与分析。

近似熵是一种量化信号复杂度的统计指标，在脑电信号的研究中得到了充分的体现。Seyyed Abed Hosseini提取了FP1，FP2，T3，T4和Pz等电极EEG 信号的ApEn作为特征，利用支持向量机（support vector machine，SVM）算法进行情感识别，正确率达到了73.25%［2］。Jianping Liu等用EEG 信号的ApEn 为特征，利用KPCA－HMM（kernel principal component analysis and hidden Markov mode）模型识别精神疲劳，准确率达到了84%［3］。尽管近似熵被广泛地用于脑电信号的复杂度分析，但是它也存在如下缺点：近似熵的值与数据长度有关；近似熵缺乏相对一致性。样本熵是由Richman提出的一种新的时间序列复杂性测度方法，比近似熵需要更少的数据量。不同领域的学者用样本熵在脑电数据上也做了大量的研究。Yuedong Song等提出一种优化的样本熵算法，利用该算法计算出EEG 信号的样本熵，并以其为分类特征，然后利用ELM （extreme learning machine，ELM）来识别癫痫发作，最高准确率达到99.00%［4］。周鹏等提出了基于脑电信号的样本熵特征进行运动想象分类的思想，并利用Fisher线性分类器对基于样本熵的左右手运动想象进行了动态分类，得到的平均最大分类正确率达到87.8%［5］。燕楠等提出利用样本熵作为特征进行注意力相关脑电信号的分析与分类处理，并采用支持向量机 （SVM）算法进行分类，其分类准确率可达85.5%［6］。

大量的研究结果表明，近似熵和样本熵在脑电信号上有很好的应用前景。但是哪种算法对于分析处理脑电信号更合适，需要更深入的讨论与研究。Roldan等的研究指出样本熵和近似熵均能明显地区分出正常人和癫痫患者的EEG 信号，但当样本大幅度丢失时，样本熵比近似熵显示出更健壮的性能［7］。白冬梅等研究指出癫痫发作时近似熵值和样本熵值均会显著的减小，但样本熵值的变化幅度会明显的大于近似熵，且样本熵值的变化幅度相比较于近似熵提高了大约15%～20%［8］。目前在脑电数据上近似熵和样本熵的对比研究还相对较少。论文通过两组公共数据集讨论近似熵与样本熵哪种更适合作为脑电特征。

1 近似熵和样本熵

1.1 近似熵

近似熵是20世纪90年代初由Pincus提出的，其物理意义是当模式维数m 发生变化时，时间序列产生出新模式的概率大小，产生出新的模式概率越大，序列复杂程度就越大，相对应的近似熵值也就会越大。假设原始信号序列为x（1），x（2），…，x（N），预先给出模式维数为m 和相似性容限为r，则近似熵的具体算法如下：

步骤1 将序列x（1），x（2），…，x（N）按顺序组成m 维矢量，即

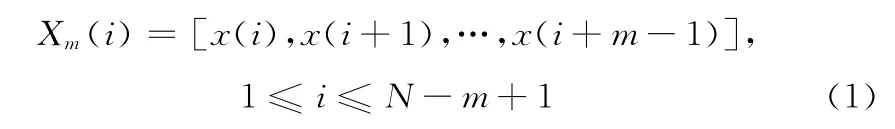
步骤2 定义矢量Xm（i）与矢量Xm（j）之间的距离为d［Xm（i），Xm（j）］，即

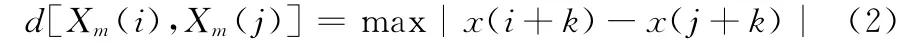
步骤3 给定相似容限r（r＞0），对于每个1≤i≤Nm＋1，统计出d［Xm（i），Xm（j）］＜r的数目与矢量总数Nm＋1的比值，记作

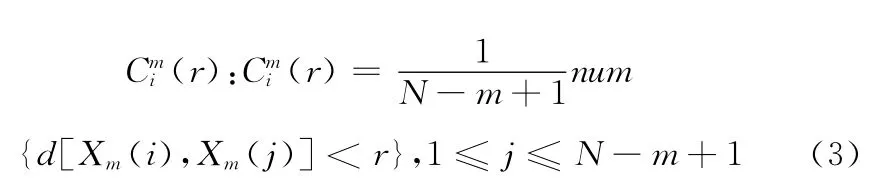
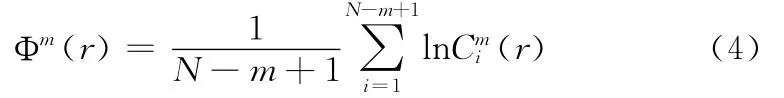
步骤5 再把维数m 加1，变成m＋1，重复步骤1到步骤4的过程，得到（r）和（r）

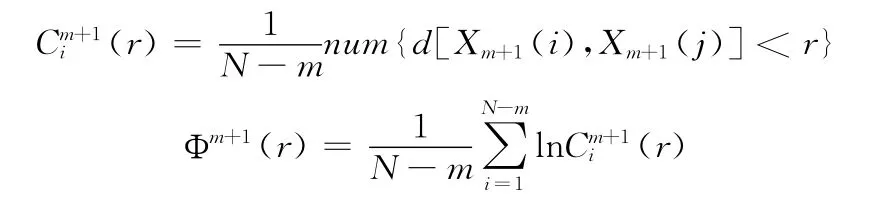
步骤6 此序列的近似熵为

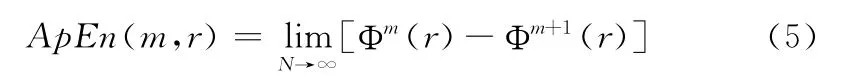
但是在实际计算中N 不可能为∞，当N 取有限值时，估计

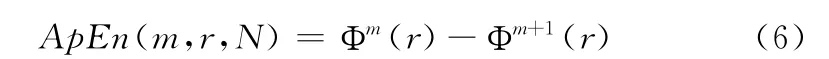
1.2 样本熵

样本熵是由Richman提出的一种新的时间序列复杂性测度方法，是近似熵的一种改进算法。

样本熵的具体算法如下：

步骤1 将序列x（1），x（2），…，x（N）按顺序组成m 维矢量，即

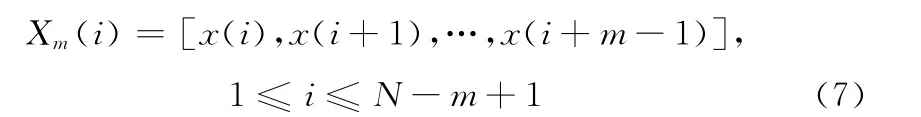
步骤2 定义矢量Xm（i）与矢量Xm（j）之间的距离为d［Xm（i），Xm（j）］，即

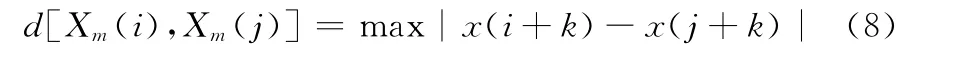
步骤3 给定相似容限r（r＞0），对于每个1≤i≤Nm，统计出d［Xm（i），Xm（j）］＜r 的数目与矢量总数Nm－1的比值，记作

式中：1≤j≤N－m，i≠j。求其对i所有的平均值

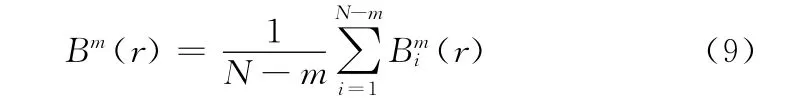
对于m＋1点矢量，同样有

式中：1≤j≤N－m，i≠j。求其对所有i的平均值

步骤4 此序列的样本熵为

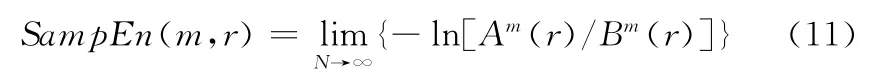
但是在实际计算中N 不可能为∞，当N 取有限值时，估计

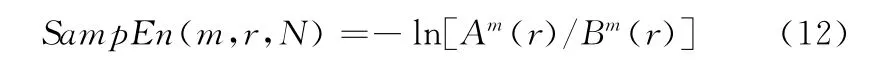
1.3 近似熵与样本熵理论上对比

为了便于分析，设B 为维数为m 时，序列的自相似概率；A 为维数m＋1时，序列的自相似概率，得出CP＝A／B［8］。从近似熵算法能够看出，近似熵的计算是以－ln（CP）为模型，并且计算出了所有模型的平均值。为防止出现ln（0），近似熵的计算过程中明显的比较了自身数据段，这种方式与新信息观点是不相容的，所以一定会存在偏差。而样本熵计算的是和的对数，所以样本熵算法中不包含自身数据段的比较，其优势在于包含更大的A、B，以及更加准确的CP 估计，因而样本熵的计算不依赖数据长度。所以，样本熵在理论上比近似熵有更高的精度。

相比较于近似熵算法，在样本熵算法中除了没有包括统计矢量自匹配这一差异外，其它的步骤与近似熵算法类似，但是计算时间上可以节约一半［9］。

2 实 验

理论上，样本熵是近似熵的一种改进算法。论文通过两组公共数据集讨论近似熵与样本熵哪种更适合作为脑电特征。一组数据是DEAP数据集关于情绪识别的脑电数据；另一组数据是UCI数据集关于嗜酒成瘾者与正常人的脑电数据。

从近似熵和样本熵的算法中，可以看到ApEn（m，r，N）、SampEn（m，r，N）的值与参数m，r和N 的选取有关。Pincus建议计算近似熵时，嵌入维数m 一般取1 或2，相似容限r一般在0.1SD～0.25SD 之间（SD 为时间序列的标准差），数据点数N 最好在100～5000之间。在论文中，计算近似熵和样本熵时，m 取2，r取0.2SD。

2.1 实验一

2.1.1 实验数据

DEAP数据集是供基于生理信号进行情绪识别研究的一个开放数据库［10］，该数据库包含32名被试观看40段音乐视频时的EEG 数据。这些视频均具有明显的情绪刺激作用，每段视频呈现1分钟。在数据采集之前，这些视频已经通过一些行为实验进行了情绪标注，标注方式采用通用的VAD（valence－arousal－dominance）模型，包含3个维度，其中V 表示愉悦度，A 表示唤醒度。被试在观看视频的同时，根据自身的情绪体验，对所观看的视频进行了VAD 每个维度的9点量表评价。根据V 和A 的取值，这些视频被划分为高唤醒高愉悦（HAHV）、低唤醒高愉悦（LAHV）、低唤醒低愉悦（LALV）、高唤醒低愉悦（HALV）4种类型的情绪，分别用1到4来标记这4类情绪。

EEG 信号的采样频率为512Hz，共采集40个通道（其中包括32个脑电信号通道）。该实验使用DEAP 数据集网站提供预处理之后的数据，共包含32（被试）＊40（视频）的EEG 数据。预处理后采样频率将为128Hz，采样时长为63s，包括3s的基线以及1分钟观看视频的EEG 数据。这些EEG 数据已经进行过伪迹去除和滤波处理，滤波后保留4.0－45.0Hz的数据。

2.1.2 实验结果

由于每一个视频均包含两个VAD 值，一个来自于行为实验的标注，一个来自于被试在EEG 采集过程中的标注。考虑到被试在实验过程中可能由于特殊原因导致自己标注的VAD 值不能准确反映真实的情绪，本实验选取了行为实验与被试标注一致的视频。表1为筛选后剩余的视频情况。

表1 数据筛选结果

另外，考虑到被试观看视频的情绪启动时间与疲劳效应，本实验去掉了前23s以及后20s的EEG 数据，只保留了中间20s的EEG 数据，共包含2560个时间点。实验中采用小波包分解进行数字滤波［18］，保留13－30Hz的β波段信号。滤波之后，计算每段数据的近似熵和样本熵。

由于电极安放位置不同，不同电极体现了不同脑神经细胞群的电生理活动。因此，并不是所有电极都能有效地反映不同情绪状态的差异，因此本实验期望通过筛选出差异比较显著的电极，来反映出情绪活动主要体现在哪些脑区。苗［12，13］等使用配对t检验筛选电极，但是该方法的前提是样本服从正态分布。经过分析，EEG 的近似熵与样本熵并不符合正态分布，不能直接使用配对t检验进行显著性差异检验。K－S（Kolmogorov－Smirnov）检验不要求样本服从正态分布，不仅能够检验单个总体是否服从某一理论分布，还能够检验两个总体分布是否存在显著差异。经验证是一种有效、稳定的非线性检验统计量，对噪声信号具有较强的抗噪能力，且对非线性信号具有较高的敏感性［14］。因此，本实验采用K－S双样本检验来筛选存在显著性差异的电极。

本实验分析了HAHV－HALV 两类情绪存在显著性差异的电极。采用K－S检验分析每个电极近似熵的差异显著性，并没有发现存在显著性差异（即p＜0.05）的电极；而采用K－S检验分析每个电极样本熵的差异显著性，存在显著性差异的电极分布情况见表2。

表2 HAHV－HALV 两类情绪样本熵值存在显著差异的电极

实验结果表明：使用近似熵对每个电极做显著性差异分析，并不能发现情绪识别活动存在的电极；而使用样本熵对每个电极做显著性差异分析，发现F3、CP5、FP2、Fz、FC2等电极所在的脑区对情绪活动影响显著。

2.2 实验二

2.2.1 实验数据

采用的嗜酒成瘾者（alcoholism）和正常被试的脑电数据集是美国加州大学信息与计算机科学系的公共EEG 数据集（1999年UCI KDD文件）［15］。实验参与者一共122人，每个参与实验的被试均进行了120次试验，每一次试验均对被试进行视觉刺激，刺激源来自于1980 Snodgrass 和Vanderwart图片集。在实验过程中，依据国际电极放置标准在参与实验被试的头部安放64导电极，脑电设备的采样率是256Hz，每一次的试验均记录了1s的脑电信号。但是因为数据集中的脑电信号不太完整，部分实验数据并没有被记录或已经损坏，所以为了能保证本研究中分析结果的可比性，随机的从数据集中选取了数据完整的30个嗜酒成瘾者和30个正常被试的脑电数据作为本研究中分析的两组EEG 数据［16，17］。

2.2.2 实验结果

首先，对选出的60个被试的第50次试验的64导电极EEG 数据，分别计算近似熵和样本熵的值。其次，采用KS检验分析每个电极近似熵和样本熵的差异显著性（p＜0.05），分别记录下近似熵和样本熵在64导电极中存在显著性差异的电极。然后，根据K－S检验结果，分别选用存在显著性差异电极的近似熵和样本熵形成识别嗜酒成瘾者和正常人的特征向量。最后，采用SVM－Weight算法进行嗜酒成瘾者和正常人分类，并采用3折交叉验证以及LOPO（leave one person out）两种验证方式。

图1反映了20次3折交叉验证的实验结果。其中，3折验证中以近似熵为特征的平均分类准确率为74.25%，而以样本熵为特征的平均分类准确率为80.25%。

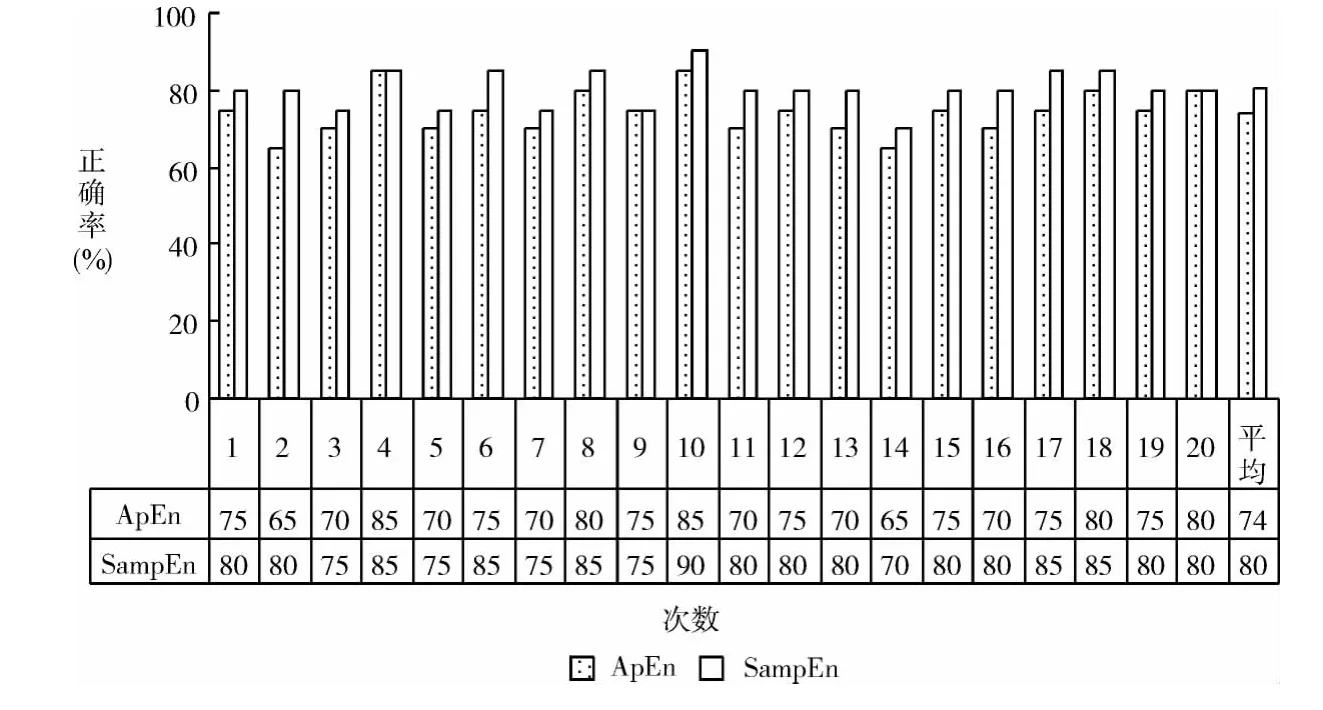
图1 3折交叉验证结果

本实验针对60个被试做了60次LOPO 验证，其平均分类准确率见表3。其中，LOPO 验证中以近似熵为特征的平均准确率为70%，而以样本熵为特征的平均准确率为73.33%。

表3 60次LOPO 交叉验证的平均准确率

2.2.3 时间复杂度对比

将被试编号为co2a0000364的嗜酒成瘾者的第000次试验的所有64导电极脑电数据作为近似熵算法和样本熵算法时间复杂度对比的测试数据。在此测试数据上，分别用近似熵算法和样本熵算法计算出近似熵值和样本熵值。图2反映了10 次近似熵算法和样本熵算法计算时间的实验结果。

从图2可以看出，对于同样的测试数据，样本熵算法的计算时间几乎比近似熵算法的计算节约一半。

3 讨 论

实验一结果表明：F3、CP5、FP2、Fz、FC2等电极的样本熵存在显著差异，这些电极主要集中在大脑前区，该结论与已有的研究结论基本一致。Petrantonakis PC［18］也通过FP1、FP2、F3、F4电极信号识别情绪；Seyyed Abed Hosseini［2］利用FP1、FP2、T3、T4和Pz等电极作为特征，取得了较好的研究效果。Sima［19］等也证实了FP2、F3、FZ等电极的另一种非线性指标——相关维也存在显著差异。

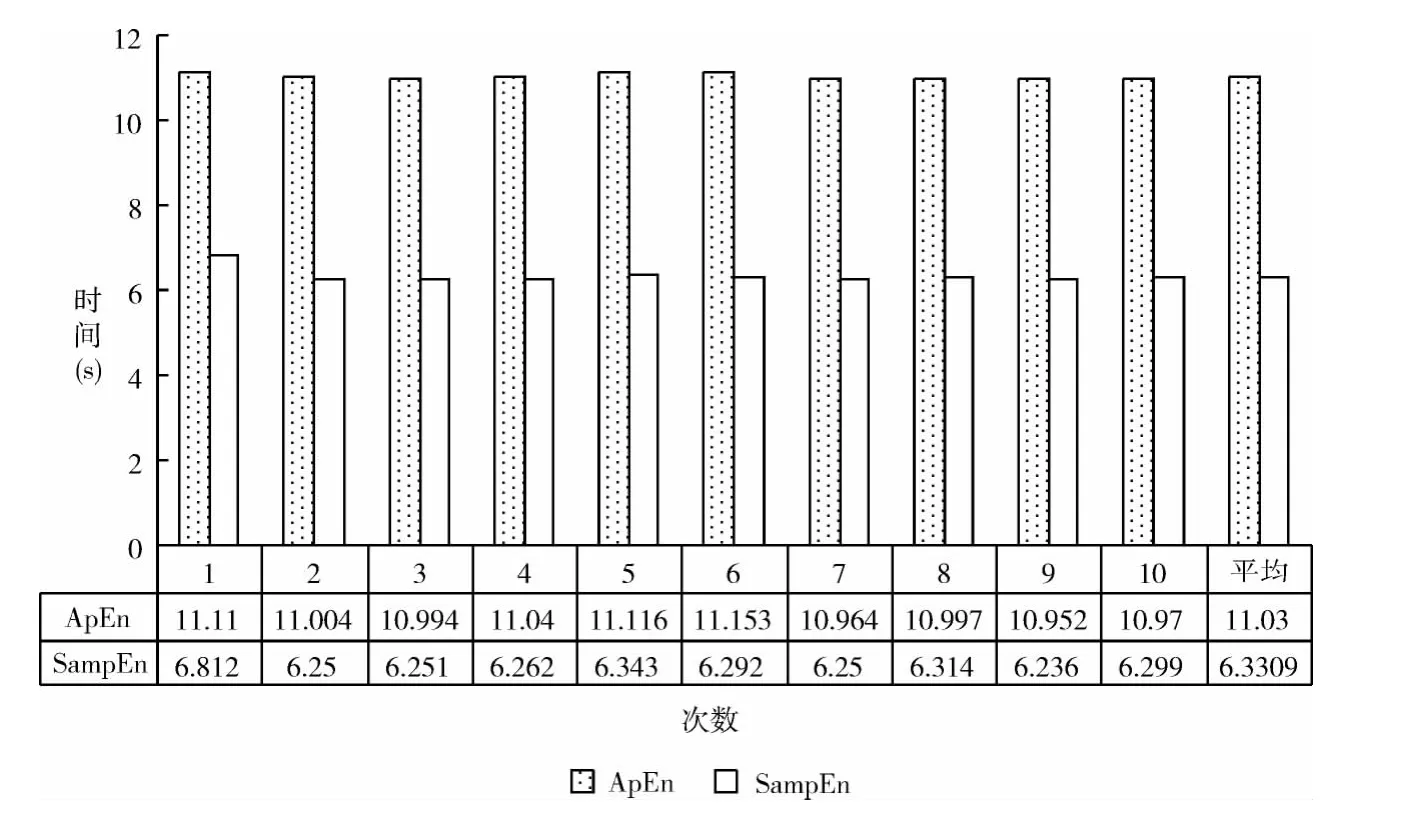
图2 近似熵与样本熵计算时间对比

实验二的分类结果表明：使用样本熵和近似熵作为特征的平均正确率均高于随机水平，说明利用近似熵和样本熵存在显著差异的电极，均能很好地识别出嗜酒成瘾者和正常人。但无论是采用3折交叉验证还是LOPO验证，以样本熵为特征的平均准确率均高于以近似熵为特征的平均准确率，说明样本熵特征更适合用来识别嗜酒成瘾者与正常人。另外，LOPO 验证结果表明：利用样本熵为特征区分嗜酒成瘾者与正常人，平均正确率为73.33%，说明该方法具有一定的泛化能力。从时间复杂度对比结果可以看出，样本熵算法的计算效率明显高于近似熵算法的计算效率，实验结果与理论也是一致的。

4 结束语

论文在两组脑电公共数据集上，讨论了近似熵与样本熵哪种更适用于作为脑电特征。实验结果表明，使用样本熵具有显著性差异的电极比近似熵具有显著性差异的电极能更好的反映出情绪活动主要集中的脑区；以样本熵为特征比近似熵为特征能更好的识别嗜酒成瘾者与正常人，并且论文中LOPO 验证的实验结果也说明了利用样本熵为特征区分嗜酒成瘾者与正常人的方法具有一定的泛化能力；对于同样的测试数据，样本熵算法的计算效率明显高于近似熵算法的计算效率。所以，对于脑电数据，甚至数据量较大的脑电数据，可以优先考虑使用样本熵来进行分析处理。当然，由于EEG 信号应用的广泛性，本研究还需要进一步深入，在其它领域的EEG 信号上继续进行近似熵与样本熵的对比研究，来支持论文的结论，即样本熵比近似熵更适合作为脑电特征。

［1］Azarnoosh M，Motie Nasrabadi A，Mohammsdi M R，et al.Investigation of mental fatigue through EEG signal processing based on nonlinear analysis：Symbolic dynamics ［J］.Chaos，Solitons ＆Fractals，2011，44 （12）：1054－1062.

［2］Hosseini S A，Naghibi－Sistani M B.Emotion recognition method using entropy analysis of EEG signals ［J］.International Journal of Image，Graphics and Signal Processing，2011，3（5）：30－36.

［3］LIU J，ZHANG C，ZHENG C.EEG－based estimation of mental fatigue by using KPCA－HMM and complexity parameters［J］.Biomedical Signal Processing and Control，2010，5（2）：124－130.

［4］Song Y，Crowcroft J，Zhang J.Automatic epileptic seizure detection in EEGs based on optimized sample entropy and extreme learning machine ［J］.Journal of Neuroscience Methods，2012，210 （2）：132－146.

［5］ZHOU Peng，GE Jiayi，CAO Hongbao，et al.Classification of motor imagery based on sample entropy ［J］.Information and Control，2008，37 （2）：191－196 （in Chinese）. ［周鹏，葛家怡，曹红宝，等.基于样本熵的运动想象分类研究 ［J］.信息与控制，2008，37 （2）：191－196.］

［6］YAN Nan，WANG Jue，WEI Na，et al.Feature exaction and classification of attention related electroencephalographic signals based on sample entropy ［J］.Journal－Xian Jiaotong University，2007，41 （10）：1237－1241 （in Chinese）. ［燕楠，王珏，魏娜，等.基于样本熵的注意力相关脑电特征信息提取与分类［J］.西安交通大学学报，2007，41 （10）：1237－1241.］

［7］Roldan E M C，Molina－Pico A，Cuesta－Frau D，et al.Characterization of entropy measures against data loss：Application to EEG records［C］／／Engineering in Medicine and Biology Society，Annual International Conference of the IEEE.IEEE，2011：6110－6113.

［8］BAI Dongmei，QIU Tianshuang，LI Xiaobing.The sample entropy and its application in EEG based epilepsy detection ［J］.Journal of Biomedical Engineering，2007，24 （1）：200－205（in Chinese）.［白冬梅，邱天爽，李小兵.样本熵及在脑电癫痫检测中的应用 ［J］.生物医学工程学杂志，2007，24 （1）：200－205.］

［9］ZHUANG Jianjun，NING Xinbao，ZOU Ming，et al.Agreement of two entropy－based measures on quantifying the complexity of short－term heart rate variability signals from professional shooters ［J］.Acta Physica Sinica，2008，57 （5）：2805－2811 （in Chinese）.［庄建军，宁新宝，邹鸣，等.两种熵测度在量化射击运动员短时心率变异性信号复杂度上的一致性 ［J］.物理学报，2008，57 （5）：2805－2811.］

［10］Koelstra S，Muhl C，Soleymani M，et al.Deap：A database for emotion analysis；using physiological signals ［J］.IEEE Transactions on Affective Computing，2012，3 （1）：18－31.

［11］HAN Qingpeng.Evaluation of human mental stress states based on wavelet package transformation and nonlinear analysis of EEG signals ［J］.Journal of Vibration and Shock，2013，32 （2）：182－188 （in Chinese）.［韩清鹏.利用EEG 信号的小波包变换与非线性分析实现精神疲劳状态的判定 ［J］.振动与冲击，2013，32 （2）：182－188.］

［12］Wang D，Miao D，Blohm G.Multi－class motor imagery EEG decoding for brain－computer interfaces［J］.Frontiers in Neuroscience，2012，6：151.

［13］Wang D，Miao D，Blohm G.A new method for EEG－based concealed information test［J］.IEEE Transactions on Information Forensics and Security，2013，8 （3）：520－527.

［14］HOU Shuyu，LI Yourong，LIU Guanglin.A new method of detecting nonlinear for time series based on KS test［J］.Journal of Electronics ＆Information Technology，2007，29 （4）：808－810 （in Chinese）.［侯澍昱，李友荣，刘光临.一种基于KS检验的时间序列非线性检验方法 ［J］.电子与信息学报，2007，29 （4）：808－810.］

［15］Tcheslavski G V，Gonen F F.Alcoholism－related alterations in spectrum，coherence，and phase synchrony of topical electroencephalogram ［J］.Computers in Biology and Medicine，2012，42 （4）：394－401.

［16］FAN Jinfeng，SHAO Chenxi，WANG Jian，et al.A comparative evaluation of nonlinear characteristics EEG for alcoholic and normal people ［J］.Chinese Journal of Biomedical Engineering，2008，27 （1）：18－22 （in Chinese）. ［范金锋，邵晨曦，王剑，等.醉酒者脑电和正常脑电非线性特性的比较评估 ［J］.中国生物医学工程学报，2008，27 （1）：18－22.］

［17］ZOU Yang，MIAO Duoqian，WANG Deng.Research on sample entropy of alcoholic and normal people ［J］.Chinese Journal of Biomedical Engineering，2010，29 （6）：939－942（in Chinese）.［邹阳，苗夺谦，王登.醉酒者和正常人脑电的样本熵研究 ［J］.中国生物医学工程学报，2010，29 （6）：939－942.］

［18］Petrantonakis P C，Hadjileontiadis L J.Emotion recognition from EEG using higher order crossings ［J］.IEEE Transactions on Information Technology in Biomedicine，2010，14（2）：186－197.

［19］Hoseingholizade S，Golpaygani M R H，Monfared A S.Studying emotion through nonlinear processing of EEG ［J］.Procedia－Social and Behavioral Sciences，2012，32：163－169.