谱分析法在路段行程时间预测中的应用

邓明君，曲仕茹，秦 鸣

（1.西北工业大学自动化学院，陕西 西安710072；2.华东交通大学土建学院，江西 南昌330013）

路段行程时间是交通诱导方案生成最重要的基础参数，也是出行者最关心的出行服务指标之一，但道路上的交通状态瞬息万变，直接用当前检测的数据制定下一时刻的交通管控或诱导方案，往往产生方案滞后于实际交通状态的结果，从而影响方案效益。若能从当前及历史检测数据中较精确地估算出将来某个时间段，如5～30分钟的路段行程时间数据，以此数据制定诱导方案，则方案的针对性和实时性将会得到提升。将此超前预报信息发布给出行者，则可使出行个体合理选择出行路径和出行方式，节约出行时间，均衡路网负荷。当前这些成果大致可分为两大类，一类是基于统计的方法，如参数回归、非参数回归［1］、自回归模型、卡尔曼滤波模型［2-3］、小波分析等［4-5］。第二类为智能学习模型：模糊预测模型［6-7］、遗传算法模型［8］、神经网络模型等［9］。这些模型或多或少都存在一些缺点，诸如需要历史数据量大、运算量大、预测速度慢、具有一定滞后性、易陷入局部极小点、泛化能力差等。

路段行程时间伴随路段流量的波动而动态变化，具有一定的随机性，同时也具有很强的规律性，对于同一条道路，全天各时段检测的行程时间可构成一个时间序列，交通流量随时间波动的随机性和规律性决定了行程时间也具有同样的随机性和规律性，路段行程时间序列可看成是一组具有一定规律的随机信号。信息理论中的谱分析方法可以揭示隐含在随机序列中的趋势信息和规律，从而实现对随机信号的估计。应用谱分析的这一功能，从看似随机的历史行程时间序列中挖掘出其波动规律，从而实现对下一时段行程时间的估计在思想上具有可行性。1974年，Nicholson andSwann［10］第一次将谱分析方法应用于交通流量预测，他将路段流量序列表示为若干正交向量的线性组合，应用最小二乘法建立了流量预测模型。虽然这一方法具有较高的预测精度，但是作者没有对这种方法做进一步的深入研究，预测精度和适应性还有进一步提高的空间。本研究在［10］基础上，应用谱分析中的分解与重构，在重构时，通过优化特征向量系数，实现对路段行程时间的预测。

1 谱分析原理

谱分析方法就是将随机序列分解为不同振幅、相位、频率的序列组合，通过这种分解，发现随机序列的主要分量成分，把握其主要变化规律，从而实现对随机序列的趋势进行估计和控制。应用于谱分析的变换有多种，其中离散Karhunen-Loeve（K-L）变换是以随机序列统计特征为基础的在均方意义下为最佳的正交变换。该变换在变换域中能量最集中，只要较少个数的系数就能恢复出精度不错的原随机序列。因此，在信号处理中得到大量的应用。

设M维间隔为k=1，2，…，N的离散随机序列信号定义为如下形式：

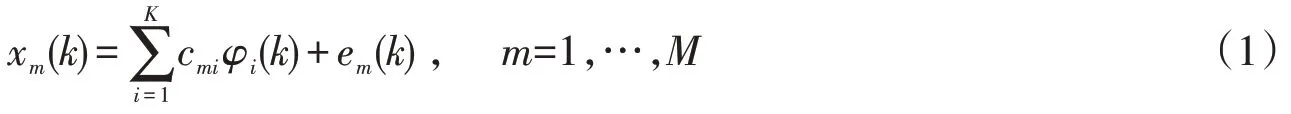
式中：xm(k)表示M维序列中第m个序列在第k个时间间隔时的值；em(k)为该时刻的误差；φi(k)为一组正交向量；cmi为对应的系数。由于K-L 变换的能量集中性，因此（1）式i的取值可做K步截断。即i=1，2，…，K。也即在有限的分解项数下，（1）式右侧就可很好地逼近xm(k)。

对（1）式用向量表示：

式中：

X=[xm(k)]，M×N

C=[cmi]，M×K

φT=[φi(k)]，K×N

E=[em(k)]，M×N

最小化误差矩阵：

因为φTφ=I，则特征向量系数矩阵：

C中的每一个元素相互独立，且对应于用于预测的互不相关的一个基。Davenport and Root［11］，发现可以用离散形式的K-L积分方程来表示随机序列协方差矩阵的分解。如式（5）

式中：

用（5）式可求得特征向量矩阵φ以及对应的特征根λi，将λi由大到小排列，其中较大特征根对应序列的主要分量，具有低频特性，表征序列的主要变化趋势特征，较小特征根对应序列的高频部分分量，体现序列的随机波动和噪音特征，文献［11］发现用部分较大特征根对应的特征向量重构原序列便可获得很小均方误差。

2 基于谱分析的行程时间预测方法

由上述原理，当求得系数C后，结合特征向量矩阵Q，由式（2）可反求时间序列，理论上，当式（1）中的k趋近与无穷时，=X。

对于同一条道路，相同工作日或周末所体现的交通相似性最强，因此，统计历史上某一个工作日该道路的15分钟间隔的平均行程时间序列值，全天共计96组数据，连续统计S周，获得一个S×96的历史序列矩阵，由（6）、（5）、（4）式可求得S×K维的系数矩阵Ch以及对应的特征向量矩阵φ。当前时段之前检测序列也对后续时段行程时间产生影响，为在预测中体现这种影响，构造一个新序列Xc，用以计算当前检测序列的特征向量系数Cc。

Xc=(T1,T2,...,Tt,Tt+1)，其中，T1～Tt为当前检测序列，Tt+1为对应时刻历史均值，由（4）式求得1×K维的系数向量Cc，将Ch与Cc合并为（S+1）×K维的矩阵C，并对C的行向量加权求和，得1×K维的系数加权和向量Ca，由（2）式可求得t+1个时间间隔的流量序列。

式中：W为组合权重向量。

由于距离当前时间越近的时段，其之间的相关性越强，反之则越弱，因此，预测中只考虑当前时段之前的A个时段的历史及当前检测数据，以减少不必要的计算量。对特征向量矩阵φ滚动处理可实现这一目标。即在求特征向量系数Cc时，选取特征向量

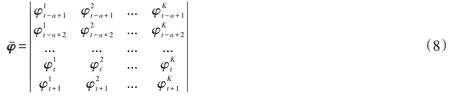
选取当前检测序列

3 Ca 合成的权值优化

Ch中的每行元素都由对应的一个历史序列计算而得，而当前要预测的序列与每一个历史序列存在相似性，合成中与当前检测到的序列越相似的历史序列，其对应的变换系数向量应占有较大权重，基于此，以当前检测序列与对应时段历史序列值之间的欧氏距离来描述其相似性。设当前检测值与各历史序列对应值的欧氏距离为d(i)，则Ch中各行的权重向量

式中：d(i)=；xc为当前检测序列；xhi为第i个历史序列，时间段为当前时段t及之前的A个时段。历史序列综合系数向量Ctmp=WCh，最终合成特征向量系数：Ca=αCc+(1-α)Ctmp，0 ≤α≤1。其中α的取值可根据实际情况确定。

4 预测流程

本方法的实现步骤如下：

1）读入历史行程时间序列矩阵Xi

2）计算历史行程时间序列相关性矩阵R

3）计算R矩阵的特征向量φ和特征根λ

4）计算特征向量系数Ch=Xφ

5）计算当前序列特征向量系数Cc=Xcφ

6）确定回朔时段A，在回朔时段内计算当前序列与对应时段历史序列的欧式距离，合成特征向量系数Ctmp=WCh

7）计算最终合成特征向量系数Ca=αCc+(1-α)Ctmp

8）做一步预测，确定时间窗为（A+1），在时间窗内选择对应的特征向量子矩阵，计算时窗内序列的估计值

10）当有新检测数据进入时，时间t=t+1，更新Xc返回（5）。

5 应用实例

利用南昌市洪都大桥连续六周，星期二检测的15分钟间隔行程时间数据应用本文介绍方法进行行程时间预测，其中前五周的数据作为统计分析的历史数据，第六周的数据为检验数据。预测中分别选取不同的回朔时段A的取值进行预测。为分析预测精度，分别选取平均相对误差，均方根误差，均等系数等指标对预测结果进行分析，在Matlab平台上，实现本文方法，输出的各误差指标如表1。

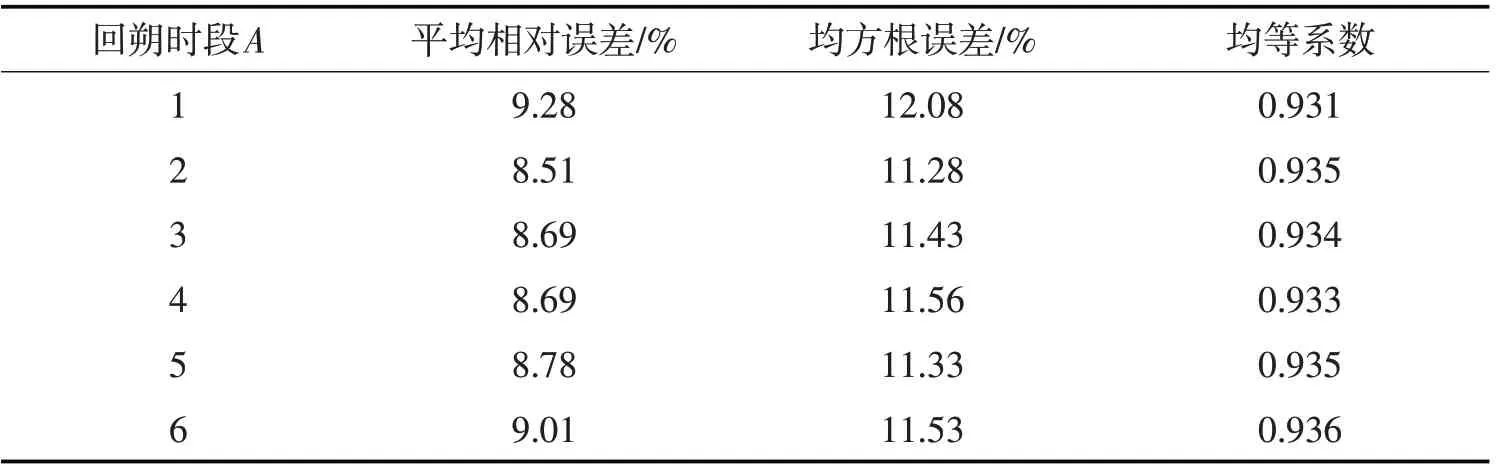
表1 预测数据统计表Tab.1 The prediction results

由上表可见，当回朔时段数是2时，各指标数据相对较好。为验证本方法与当前其他行程时间预测研究成果的性能，应用基于自组织映射及BP神经网络［12］方法预测本文第六周的数据，将前五周的每连续的8个序列作为一组输入模式，类别数为6，先进行自组织分类学习，输出为分类结果，而后对各分类，应用BP神经网络训练，用训练好的网络预测第六周的行程时间数据。本文方法与文献［12］方法预测曲线如图1。

图1 预测值与实测值对比图Tab.1 Comparison chart between prediction and detection

由图1 看出，在波动较大时段，两种方法的预测误差都相对较大，而平稳时段两种方法均拟合良好。用EPPR=来计算各时刻预测值得相对误差，绘制图2，其中是预测值，x(i)是实测值。由图2看出，本文方法在高峰时段，误差较大，部分预测周期，误差超过30%，但在平峰时段，其误差情况要好于文献［12］。比较两种方法EPPR的均值，本文方法为8.51%，文献［12］方法为7.78%。总体看，文献［12］的稳定性和精度均略好于本文方法。

在计算效率上，同样的基础数据和验证数据，本文方法从读入数据到滚动完成96个验证数据耗时仅需0.836 s，而在同一台电脑上，同样基于matlab平台，文献［12］完成自组织分类，耗时22.461 s，训练网络耗时27.895 s，应用训练好的网络完成预测耗时0.677 s，文献［12］完成预测总耗时51.033 s。显然，本文方法的计算效率要远好于文献［12］。

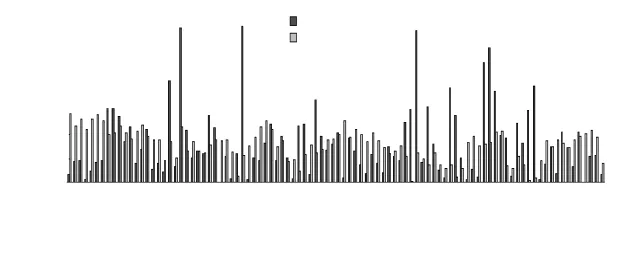
图2 全天预测误差分布图Tab.2 Prediction error distribution for the whole day

5 结论

将谱分析中的分解与重构思想应用于短时行程时间预测，其基础数据仅需要较少的对应时段的历史数据，如在本实例计算中，回朔时段为2时，可获得最好的预测精度，即只需要当前时刻前两个时段的历史数据就可进行预测、与现有成果相比计算效率高。从预测精度来看，预测相对误差为8.51%，处于现有成果的中等水平，从均等系数看，预测的均等系数都在0.9以上，这说明预测值与实测值还是有较好的拟合。当然该方法还有进一步优化的空间，比如，如何进一步利用分解、重构对时间序列特征的记忆和再现功能，如何从历史序列的纵向和横向两个方面，挖掘数据的相关性，优化历史序列特征向量系数，使最终系数能够更精确地体现当前交通状态和其变化趋势，以便获得更高的预测精度，同时如何扩展使该方法能够完成多步预测。

[1]DAVIS G A, NIHAN N L., Nonparametric regression and short-term freeway traffic forecasting[J]. J. Transp. Eng, 1991,117(2):178-188.

[2]张玉梅,曲仕茹,温凯歌.基于混沌和RBF神经网络的短时交通流量预测[J].系统工程,2007,25(11):25-30.

[3]沈国江,王啸虎,孔祥杰.短时交通流量智能组合预测模型及应用[J].系统工程理论与实践,2011,31(3):561-568.

[4]BIDISHA G,BISWAJIT B,MARGARET O’M.Random process model for urban traffic flow using a wavelet-bayesian hierarchical technique[J].Computer-Aided Civil and Infrastructure Engineering,2010,(25):613-624.

[5]冯金巧,杨兆升,孙占全,等.基于小波分析的交通参数组合预测方法[J].吉林大学学报:工学版,2010,40(5):1220-1224.

[6]YIN H, WONG S C, XU J, et al. Urban traffic flow prediction using a fuzzy-neural approach[J]. Transp. Res. Part C: Emerging Technol.,2002,10(2):85-98.

[7]李庆奎,吕志平,葛智杰.基于模糊综合评判的智能行程时间预测算法[J].华东交通大学学报,2012,29(4):6-10.

[8]SU HAOWEI, YU SHU. Hybrid GA based online support vector machine model for short-term traffic flow forecasting[C]//APPT 2007,LNCS 4847,pp.743-752.

[9]SONG GUOJIE,HU CHENG,XIE KUNQING,et al.Process neural network modeling for real time short-term traffic flow prediction[J].Journal of Traffic and Transportation Engineering,2009,9(5):73-75.

[10]NICHOLSON H, SWANN C D. the prediction of traffic flow volumes based on spectral analysis[J]. Transpn Res, 1974(8):533-538.

[11]DAVENPORT W B,ROOT W L.An introduction to the theory of random signals and noise[M].New York:McGraw-Hill, 1958:1-4.

[12]龚勃文,林赐云,李静,等.基于核自组织映射-前馈神经网络的交通流短时预测[J].吉林大学学报:工学版,2011,41(4):938-943.