基于分类预处理的协同供应商模糊综合评价
黄细燕,徐玉萍
(华东交通大学轨道交通学院,江西 南昌330013)
专业化和集约化的社会化大生产要求供应链的核心生产企业专注于自身核心业务,而将非核心业务外包,因此,供应商选择对核心企业的利益和发展具有重大影响,是企业供应链研究的重点和热点课题。
供应商选择是供应链管理[1]的重要问题之一,在上世纪较早时期就得到了国外研究者的关注[2];国内学者也在供应链合作伙伴的评价指标体系与评价问题上紧随外国研究开展了大量有效工作[3]。供应链协同对提高生产效率和整体具有重要作用,越来越受重视[4]。模糊综合评价方法是供应商评价与选择研究时很受欢迎的方法,其思想来自层次分析法(AHP),它综合了模糊理论和AHP方法的优点,能较好克服主观影响,是定性与定量结合的分析方法。许多工作利用各种模糊数来定量刻画事物属性,结合多层次多属性决策方法进行决策分析[5-6],但构造隶属函数不太容易且有一定主观色彩。为此,引入模糊互补矩阵,通过优先关系系数定量地描述待优选的若干方案在每一个因素下的优劣,避开了各个等级隶属度的确定问题。为了克服判断矩阵与人类思维之间的一致性差异,引入模糊一致矩阵[7]。模糊一致矩阵具有中分传递性,符合人类思维的一致性,可以保证优选结果的合理性。
模糊综合评价方法及其应用研究,较少对指标数据按定性与定量等不同类型进行分类预处理,本文将所有指标分为3类,利用梯形模糊数预处理其中一类定性指标,以设计评价指标的预处理方法;然后,对定性指标与定量指标采用不同方法构建模糊互补矩阵,并计算模糊一致矩阵,进而构建了面向协同管理的供应商模糊综合评判方法。在对某核心生产企业的5个待选择供应商企业的相关定量指标计算和定性指标模糊打分基础上,利用该综合评判方法,计算得到各供应商的综合评分,为供应商选择提供了客观、科学的决策依据。
1 协同管理中供应商选择的评价指标体系
供应商选择存在于供应链伙伴关系构建与维系的全程,建立良好伙伴关系是供应链协同管理的重要保障。核心生产企业对供应商的选择需要按照供应链协同管理的总体战略目标和资源计划的要求,以快速响应市场需求变化和提高市场竞争力为目标做出正确的决策。依据目的性原则、客观科学性原则、简明现实性原则、全面性、系统性原则、稳定可比性原则、通用性与发展性相结合原则等,构建了供应商选择的评价指标体系。供应商选择指标体系具有3个层次,把除最末层次之外的多于一个指标的其他层次视为由若干子系统构成,指标体系的第一层次视为由3个子系统即U1 产品竞争力、U2 同步协作能力以及U3 供应商企业总体状况构成,各子系统包括若干个二级子系统,而各二级子系统包括若干个第三层次的评价指标。一级评价指标3个,二级评价指标12个,三级评价指标共计29个。
U1 的下属指标IU1={U11 产品质量,U12 产品成本,U13 产品开发能力,U14 生产能力};IU11={U111 产品合格率,U112 产品抽样合格率和全检合格率,U113 返修退货率,U114 ISO 认证情况,U115产品匹配度};IU12={U121 产品获得成本,U122 数量折扣率,U123 降低成本计划,U124 成本投入产出比};IU13={U131 新产品开发周期,U132 产品开发成功率,U133 产品主动更新率};IU14={U141 生产批量要求,U142 生产线要求,U143 产品平均出产周期与同类产品周期比};IU2={U21 柔性,U22 交货,U23 信息技术能力,U24 合作兼容性};IU21={U211 数量柔性,U212 时间柔性,U213 品种柔性};IU22={U221 准时交货率,U222 订货满足率,U223 订货提前期,U224 订货批量};IU23={U231 信息集成度,U232 生产管理信息系统应用程度,U233 信息共享程度};IU24={U241 战略目标兼容性,U242 企业文化兼容性};IU3={U31 生产历史,U32 信誉度,U33 合作态度,U34 地理位置与交通}。
2 面向供应链协同管理的供应商模糊综合评价及其步骤
传统模糊评价常用单一方法,即把所有指标放在一起处理,这可能会掩盖部分指标的重要属性。因此,对评价指标体系中的不同定量指标和定性指标的原始数据进行分类分组处理,并结合梯形模糊数建立模糊互补矩阵和模糊一致矩阵,最后计算得到综合优劣次序。
步骤1定性与定量指标原始数据的分类预处理。
首先,在指标选择及数据收集整理过程中,指标体系的构建思路是尽量选择或通过处理使指标变为可直接比较的0~1范围内的参数作为评价指标。若指标取值在0~1范围内如U115,U233,则不作进一步处理。其次,对统计值大于1的评价指标如:U121,U131,U223等指标,按照一定的参考标准分为5个模糊等级,各等级对应的分值为以0.9,0.7,0.5,0.3,0.1为中位数的长度为0.2的区间,若相应指标值落在某区间,则取指标值为区间中位数。
对指标体系中其他定性指标,利用梯形模糊数及其运算规则,通过属性值规范化和取均值对这些指标进行量化和无量纲化。具体步骤如下:
1)设定性指标属性集为X={x1,x2,…,xn},方案集(专家集)为U={u1,u2,…,um}。m位供应链协同相关专家参考语言变量评价与梯形模糊数的关系对定性指标进行评分[8],得到各定性指标xi对应各专家uj的梯形模糊属性值=(aij,bij,cij,dij),aij<bij<cij<dij是区间[0,1]之间的实数。
由于供应商协同评价指标体系中的定性指标具有不同的量纲形式,且对系统总目标有正面和负面等影响(分别称为正指标和负指标),因此,为了消除不同物理量纲形式对决策结果的影响,根据梯形模糊数运算规则,对正指标和负指标分别按照(1)式和(2)式,将梯形模糊属性值转换为规范化梯形模糊属性值矩阵,其中,矩阵的元素=(αij,βij,γij,δij)仍是梯形模糊属性值。说明:与不是向量,而是一组数构成的序列。
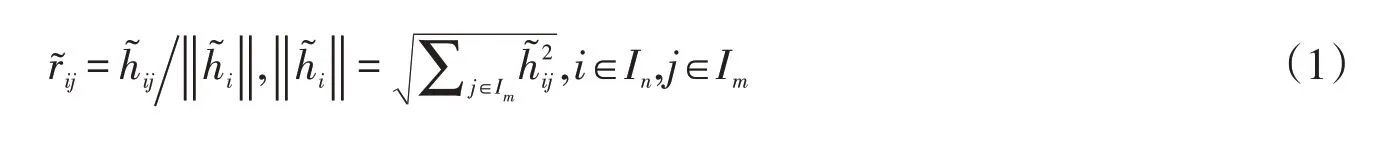
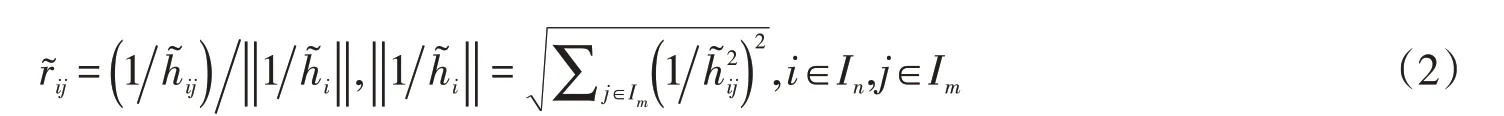
2)计算各定性指标对应各专家的去模糊化值zij=(αij+βij+γij+δij)4,并取∑j∈Imzij m为该供应商企业对应指标xi的评分值。
步骤2建立模糊互补矩阵。
要在M个指标下优选N个方案,建立M个单因素模糊互补矩阵R=(rikj)N×N,k=1,…,M,其中,rikj为在指标uk下Pi与Pj之间的优先关系系数。模糊互补矩阵是每一层次中的因素针对于上层因素的相对重要性两两比较结果所得的矩阵。对定性指标,按(3)式确定模糊互补矩阵R=(rij)n×n[7]。
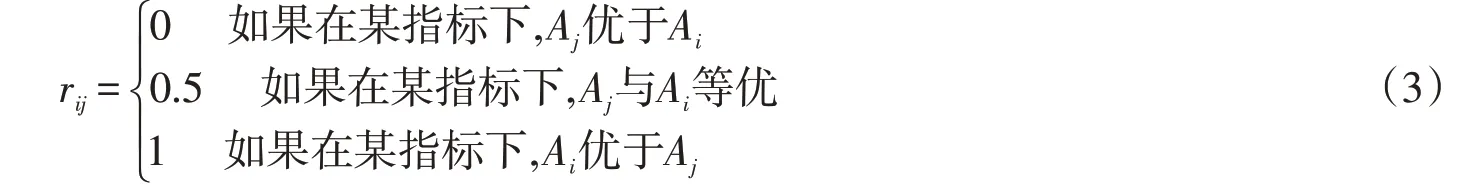
式中:rij为在某指标下Pi与Pj之间的优先关系系数。
在某一因素下,若采用这种方法,两个方案之间的优先关系系数的确能够反映两个方案的优劣,但却不能体现定量指标优劣的差异程度;而根据Suykens 与Vandewalle[9]研究表明,根据模糊一致判断矩阵的元素与权重的关系式给出的排序方法具有较高分辨率,能提高决策的科学性。并且,利用模糊一致矩阵可避免AHP方法的一致性检验。因此,仍采用0.1~0.9标度表示rij(满足rij+rji=1),将因素间两两重要性比较rij与因素重要程度权重wi,wj之间的关系表示为rij=0.5+( )wi-wj β,0 <β≤0.5,取β=0.4,易见Pi,Pj等优时有rij=0.5,Pi优于Pj时有rij>0.5。这样,便可以体现它们之间的差异程度。为了充分发挥定量指标在精确优选供应商中的作用,将对定量指标如U111采用这种方法确定rij;而对定性指标如U114,在大量专家调查的基础上给出评分等级,再采用前一种方法确定rij。
步骤3建立模糊一致矩阵。
将模糊互补矩阵通过变换改造成模糊一致矩阵FR=(rij)N×N,rij=α(ri-rj) (2n)+0.5,i=1,2,…,N,α=1 ∈( 0,1] 。矩阵FR=(rij)N×N满足:∀l=1,...,N,有rij=ril-rjl+0.5,i,j=1,…,N。
步骤4计算优度值。
首先,选择采用幂法计算供应商Pi在因素uk下的优度值。然后,计算各供应商关于指标子系统的综合优度值Wi,即将各层次间的重要性权值转化为相对于总目标的综合权重,并按Wi,i=1,…,N排序,得到N个供应商关于所有因素的综合优劣次序。
3 案例分析
某核心生产企业在进行供应链协同生产与管理时需要考察5个供应商企业P1,P2,P3,P4,P5,选取具有促进供应链协同潜质的企业。对供应商各三级指标分类获取数据,在利用梯形模糊数处理定性指标时,邀请m=5 位企业协同管理专家进行打分,所得数据如表1所示。
假定各层次的各个指标的权重值如下:一级评价指标权重为A=(0.4,0.35,0.25);二级评价指标权重为A1=(0.4,0.3,0.2,0.1),A2=(0.25,0.35,0.2,0.2),A3=(0.2,0.4,0.3,0.1);三级评价指标权重为A11=(0.2,0.3,0.2,0.1,0.2),A12=(0.3,0.1,0.2,0.4),A13=(0.3,0.3,0.4),A14=(0.2,0.175,0.20,0.125,0.3),A21=(0.4,0.35,0.25),A22=(0.3,0.3,0.15,0.25),A23=(0.2,0.3,0.5),A24=(0.6,0.4)。
对各个二级评价指标子系统,依据初始数据矩阵,计算模糊互补矩阵、模糊一致关系矩阵,得到各子系统的单指标下优度值,例如,U11子系统中5个指标下各供应商企业对单个指标优度值如表2所示。
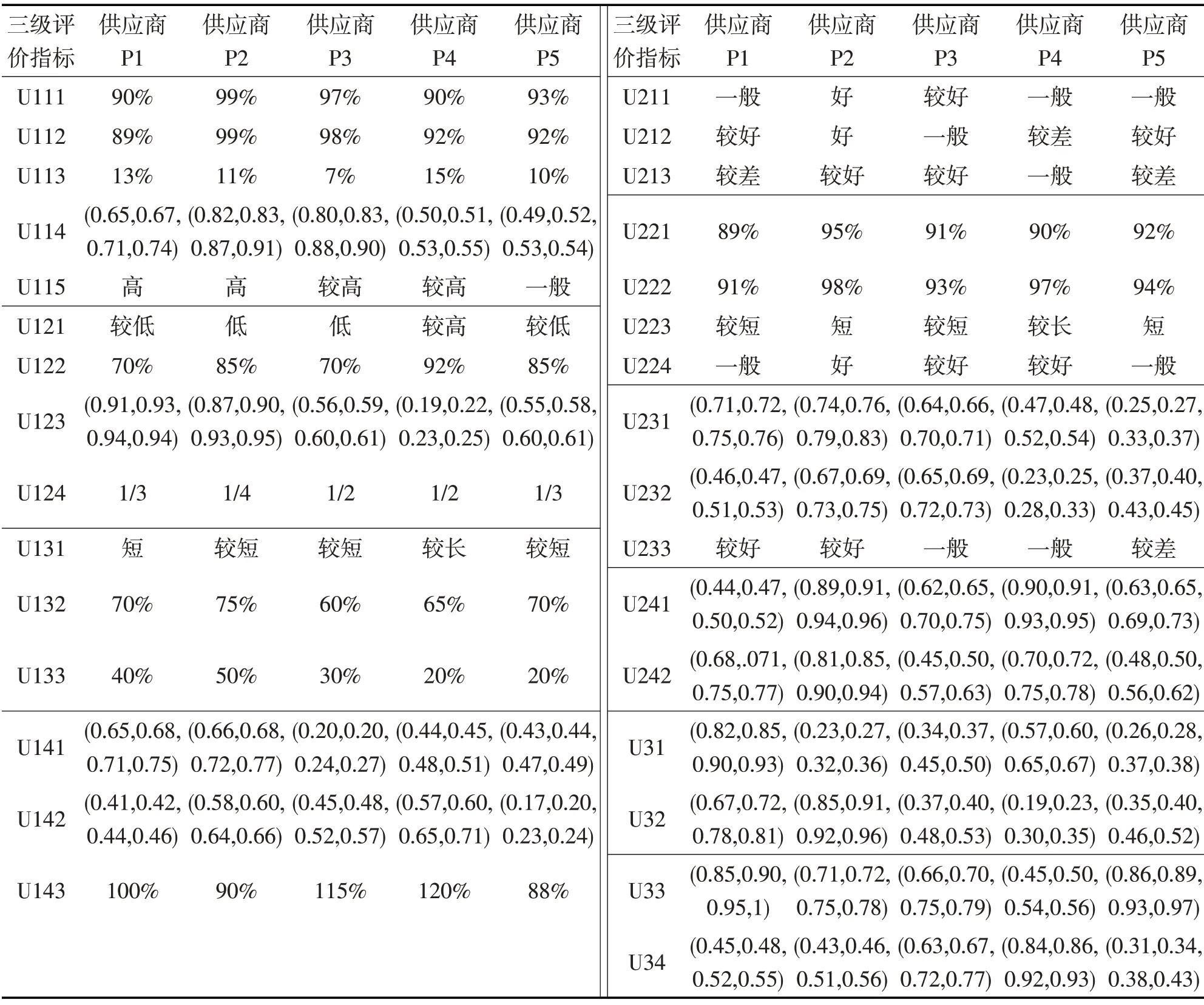
表1 面向供应链协同的供应商评价指标数据矩阵Tab.1 Supply chain collaboration oriented supplier evaluation data matrix
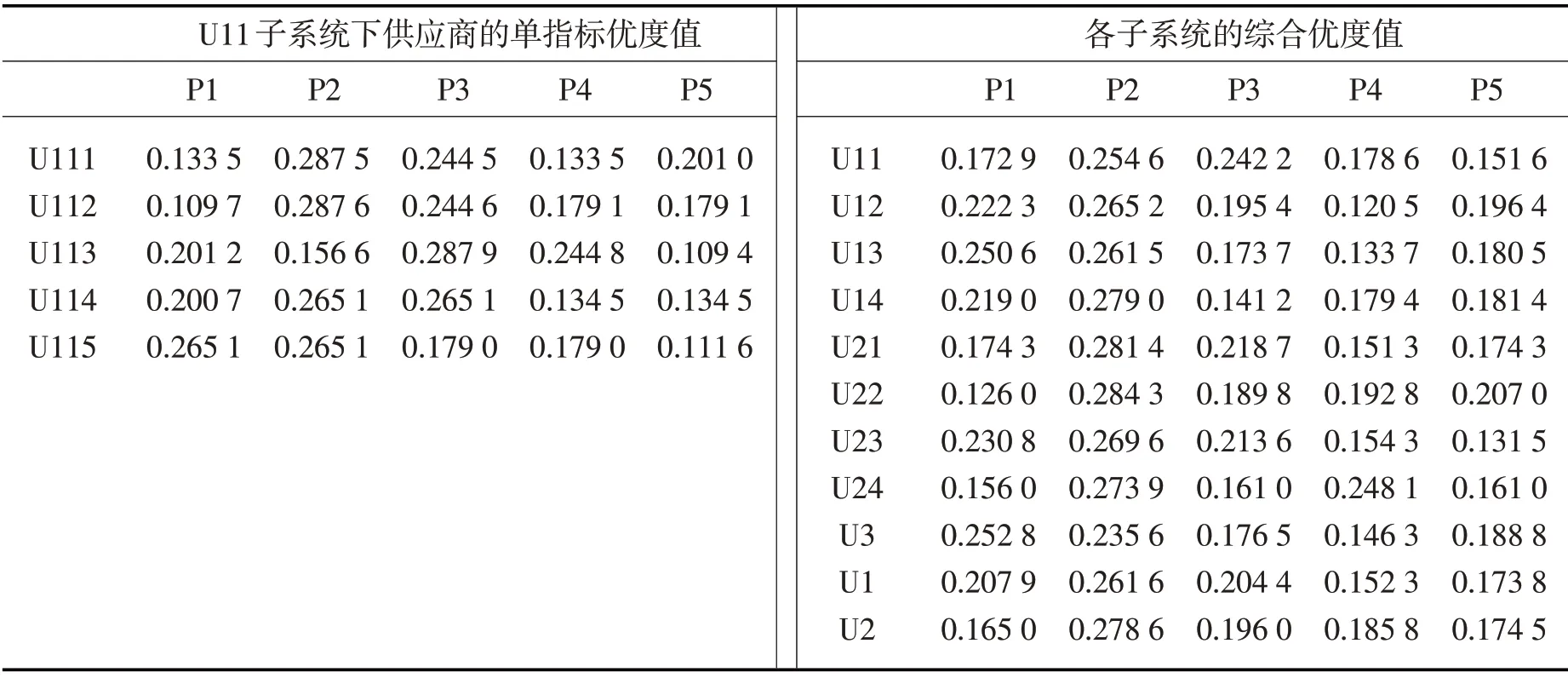
表2 单指标优度值和综合优度值Tab.2 Single index’s goodness value and comprehensive goodness value
从而,分别对各个二级评价指标子系统U11,U12,U13,U14,U21,U22,U23,U24以及U3,计算得到各子系统的综合优度值如表2所示。进一步,对各个一级评价指标子系统U1与U2,计算得到供应商企业相对各子系统的综合优度值。
最后,对所有一级评价指标子系统的综合优度值求加权和,得到供应商企业P1,P2,P3,P4,P5的综合评价分值依次为0.204 1,0.261 0,0.194 5,0.162 5,0.177 8。由此,获得所有供应商的综合排名为2,1,3,5,4,为核心生产企业面向协同生产管理的合作企业选择提供了科学合理的决策依据。
4 结论
以核心生产企业为主导的供应链协同管理,要求优选供应商节点企业,以核心生产企业自身利益与供应链集团利益最大化。基于供应商企业的产品竞争力、同步协作能力等的评价指标体系,构建面向供应链协同管理的供应商模糊综合评价方法。该方法可以克服传统模糊评判方法对定性指标处理的主观性及需要隶属度函数等缺点,主要体现在以下几个方面:
1)对原始数据的处理,充分考虑定性与定量指标、正指标与负指标的差异性等,把所有三级指标划分为3类,分别按照不同方法进行处理;特别地,对定性指标采用梯形模糊数及其运算规则进行处理。这样,在实现了无量纲化的同时,又避免了模糊评判法需要隶属度函数的缺陷。
2)区别定性指标与定量指标,结合普通的两两比较法以及模糊一致判断矩阵的元素与权重的关系式等两种方法来构建模糊互补矩阵。这样,克服了对定量指标不加区别地采用两两比较法的缺陷,提高了定量指标的分辨率。
利用所提出的模糊综合评判方法,通过计算分析得出核心生产企业的所有待选供应商企业的综合评估得分,为核心生产企业选择合适供应商提供科学决策支持。
[1] 张诚.我国供应链管理研究综述[J].华东交通大学学报,2011,28(3):92-97.
[2] DICKSON G W.An analysis of vendor selection systems and decisions[J].Journal of Purchasing,1966,2(1):5-17.
[3] LIU P, ZHANG X.Research on the supplier selection of a supply chain based on entropy weight and improved ELECTRE-III method[J].International Journal of Production Research,2011,49(3):637-646.
[4] ANBANANDAM R,BANWET D,SHANKAR R.Evaluation of supply chain collaboration:a case of apparel retail industry in India[J].International Journal of Productivity and Performance Management,2011,60(2):82-98.
[5] 迟国泰,王钰娟,刘艳萍.基于三角模糊熵的经济评价模型及副省级城市的实证研究[J].运筹与管理,2010,19(5):107-117.
[6] 虢柱,聂春龙.基于AHP分析的二级模糊综合评价模型及在边坡风险易损性评价中的应用[J].铁道科学与工程学报,2012,9(5):50-53.
[7] 姚敏.一种改进的模糊相似选择定序法[J].系统工程理论与实践,1994,14(8):18-21.
[8] 高岩,周德群,章玲,等.模糊语言群决策影响因素的分析方法[J].武汉理工大学学报:信息与管理工程版,2011,33(4):613-617.
[9] SUYKENS J A K, VANDEWALLE J.Least squares support vector machine classifiers [J].Neural Processing Letters,1999,9(3):293-300.

