无控航天器与空间碎片再入的工程预测方法研究现状

胡锐锋, 龚自正, 吴子牛

（1.西安电子科技大学 机电工程学院，西安 710071；2．北京卫星环境工程研究所 可靠性与环境工程技术重点实验室，北京 100094；3．清华大学 航天航空学院，北京 100084）

0 引言

无控航天器再入地球大气层时，在强烈的气动力和气动热载荷作用下，会发生解体并产生大量碎片；其中一部分碎片在空中被完全烧毁，其余存活下来的碎片可能会对地面建筑、人群和生态系统构成很大威胁。

人类有记录的再入事件之一发生于1997年1月22日：美国俄克拉荷马州图尔萨市的一位女士在日出前陪朋友散步，她突然看到一道火球从北向南穿过天空，之后一块碎片划过这位女士的左肩并撞击到地面。这块碎片来自于1996年4月24日发射的德尔塔火箭的第二级，与此同时德尔塔火箭第二级上的一个更大的不锈钢推进剂储箱落在德克萨斯州乔治城附近的一个农场内，此外还有一块钛制圆球落在了塞金镇外。美国1997年发射的“铱星33”通信卫星于2009年2月11日与俄罗斯 1993年发射的一颗卫星（已报废）在西伯利亚上空相撞，这是历史上首次卫星相撞事故，产生了大量碎片（约500～600 块），部分碎片再入大气层后降落在美国德克萨斯州等地。2011年9月，美国一颗名为“高层大气研究卫星”（UARS）的再入事件引起了全世界的关注和恐慌：NASA 相关专家预测UARS 坠落地球后，其碎片覆盖的区域将达到800 km 左右，而在重返地球前大约2 h，NASA才能将坠落区锁定在大约1万km之内；最终UARS于2011年9月24日坠落在南太平洋中，没有对人类产生威胁。

提前预报航天器及碎片再入轨迹和残存性是预防和减轻其危害的重要措施。近20年来，国内外在无控航天器和空间碎片再入预测方法和地面危险评估研究方面取得了很大进展，并开发了若干工程预测软件，如 NASA 的 DAS（Debris Assessment Software ）[1-2]和 ORSAT （ Object oRiented Surveillance Analysis Tool）[3]软件，ESA的SCARAB（SpaceCraft Atmospheric Re-entry and Aerothermal Breakup）[4]软件，以及国内由清华大学和中国空间技术研究院共同开发的 DRAPS（Debris Reentry and Ablation Prediction System）[5-6]软件等。

本文对航天器与空间碎片再入的工程预测方法研究现状进行跟踪和总结。

1 预测模型

1.1 航天器模型

Lips 和Fritsche[7]将航天器再入工程预测方法分为两类：基于集总参数模型的面向物体法和基于复杂表面网格模型的面向航天器法。

面向物体法中，航天器以及解体后产生的碎片外形是简单的基本几何模型，并且是集总参数类型，即其几何信息可用若干特征参数描述。工程软件DAS 和ORSAT 提供了圆球、圆柱、平板、六面体4 种基本几何模型[1-3]，DRAPS 则提供了15种基本几何模型[5-6]。面向物体法可通过定义物体之间的包含逻辑关系来模拟航天器及部件之间的多层嵌套结构。

在面向航天器法中，航天器最底层部件由基本几何模型构成，进而组成子系统，最后集成为整个航天器。基本几何模型不是集总参数类型，而是划分表面网格的三维模型。相比于面向物体法，面向航天器法不仅在几何建模水平上更接近实际情况，并且还能够准确模拟航天器的质量和惯量特性。

1.2 动力学模型

航天器几何建模方式决定所采用的动力学模型。

面向物体法由于采用集总参数的几何模型，所以采用仅确定质心运动的三自由度弹道模型，而通过预先给定的运动模式考虑物体姿态的变化对所受气动力的影响。运动模式包括静态模式和动态模式，其中静态模式中的物体再入姿态保持不变，而动态模式中的物体可绕定轴翻滚或无序翻滚，但仅考虑翻滚时的平均气动力。

与面向物体法不同，面向航天器法获得了沿物体表面的压力分布从而得到三个方向的气动力和力矩，因此采用六自由度动力学方程，即联立求解质心运动方程和姿态运动欧拉方程，计算中一般采用四元数代替欧拉角以避免求解时可能出现的奇异问题。

1.3 气动模型

钱学森[8]最早利用稀薄程度对流动进行分区。随着克努森数Kn（Kn=λ/L，λ是分子平均自由程，L是特征长度）的增加，流动可粗略分为连续流、过渡流和自由分子流三个流区，而连续流区外的其他区域一般称为稀薄流区。通常将Kn＜0.001 划分为连续流区，0.001＜Kn＜10 为过渡流区，Kn＞10为自由分子流区。航天器的再入过程经历三个流区环境，即从自由分子流、过渡流到连续流。

在自由分子流区，流场基本方程是无碰撞的Boltzmann 方程，在Maxwell 平衡气体分布假设下，可得到任意外形物体表面压力、摩擦力和热流分布的解析公式，其具体形式可参考文献[9-11]。

在连续流区，航天器迎风表面压力分布可通过牛顿流模型、切楔法、切锥法、激波/膨胀波法等近似理论或工程方法计算[12]。其中牛顿流模型方法又包括经典牛顿流模型、修正牛顿流模型等，适用于具有大撞击角的钝头外形。切楔法、切锥法和激波/膨胀波法适用于撞击角较小的楔面或锥面外形。此外，还有将牛顿流模型与切楔/切锥法组合使用的Dahlem-Buck 法，即在大撞击角时采用牛顿流模型，在小撞击角时采用切楔法或切锥法。对超声速/高超声速连续流区表面压力分布计算还可采用激波层方法或CFD 方法（无黏或有黏），但这些方法计算量太大，并不适用于航天器再入烧蚀和解体的工程预测。

由于物体形状的限制，面向物体法的气动模型给出的是整体阻力系数和平均热流大小，而不是表面压力和热流分布。在连续流区，面向物体法一般利用典型外形（如圆球或圆柱）驻点热流以及理论或实验得到的表面热流分布形式，积分平均后得到物体表面平均热流。高超声速连续流区驻点热流估算有许多成熟的近似理论或工程方法，如Lees 公式[13]、Fay-Riddell 公式[14]、Detra-Kemp-Riddell 公式[15]、Cohen 公式[16]、Sutton-Graves 公式[17]等。

在目前已有的面向航天器法应用中，表面热流分布通过与驻点参数以及撞击角有关的近似经验公式计算[4,18]。利用航天器表面网格，还可采用可信度更高的基于跟踪表面流线的边界层工程方法计算摩擦阻力和热流分布，如Dejarnette 等[19-23]提出和发展的轴对称比拟法。

在过渡流区，一方面，由于连续介质假设逐渐失效从而无法采用上述连续流区气动估算方法；另一方面，分子间的碰撞不可忽略，因此也不能通过简化Boltzmann 方程得到气动力和气动热的估算公式。工程中一般采用桥函数方法（Bridging Method），再利用连续流区和自由分子流区的结果插值得到过渡流区航天器的气动力和气动热。常用的气动力桥函数有正弦平方桥函数[24]和误差桥函数[25]。徐姗姝[26]研究了马赫数对气动力桥函数适应性的影响：在高马赫数（Ma＞10）情况下，两种桥函数都与DSMC 结果符合得较好；而在中低马赫数（Ma＜5）情况下，正弦平方桥函数偏离DSMC 结果较大，而误差桥函数与DSMC 结果仍符合得很好。

气动热桥函数有Matting 桥函数[27]和Nomura桥函数[28]。Swaminathan 等[29]给出Matting 桥函数和Nomura 桥函数对某高超声速导弹过渡区热流分布预测结果与DSMC 计算结果的对比，结论是两种桥函数均在导弹表面部分区域与DSMC 结果符合较好，但在某些区域与DSMC 结果存在明显偏差（2 倍左右）。

1.4 烧蚀和解体模型

在气动加热和辐射换热作用下，再入过程中存在从航天器表面向内部传递的净热流，该热流随着高度的降低而增大，在大约70～80 km 附近达到最大。航天器结构在长时强热作用下材料温度显著升高，一方面温度有可能达到材料熔点并使材料发生熔化，即发生烧蚀；另一方面在加热作用下结构强度降低，某些危险截面可能由于局部应力超过极限值而引起结构破坏，即产生解体。烧蚀与解体均为在强气动热效应下航天器结构的破坏现象。

在面向物体法中，为了满足对物体几何形状的限制要求，一般采用零维或一维热传导模型模拟烧蚀过程。零维模型是集总参数模型，假设物体内部温度均匀分布，不考虑热传导效应，当再入过程中的吸热总量达到物体完全熔化所需的热量后认为物体完全烧蚀（质量置零）。一维模型考虑沿物体厚度方向的热传导，将物体沿厚度方向划分一定数量的层状单元，通过建立每一层单元的热传导方程计算温度分布并模拟径向烧蚀过程。

面向物体法采用简单解体准则，包括高度准则、温度准则等。高度准则是基于对历史上再入事件的统计分析直接指定解体高度，即认为当航天器降到一定高度时则发生解体。IADC 空间碎片减缓指南[30]指出，航天器通常在75 km 高度处解体，实际观测发现航天器解体的典型高度为(80±10) km，ORASAT 软件中采用的解体高度为78 km。温度准则根据物体表面温度进行解体判断，即认为当温度升高到某一临界温度时航天器会发生解体。临界温度与物体的材料特性（如熔点）密切相关，不同部件的临界温度不同。对薄壁物体或物体壁面较厚并且再入角较大的情况，Baker 等[31]基于辐射平衡假设或考虑物体升高到临界温度所吸收的热量给出再入解体的失效温度判据表达式，其本质是临界温度为材料熔化温度的温度准则。现有的面向物体法工程软件尚未能考虑基于结构破坏的解体准则。

面向航天器法假定结构为均匀厚度的壳体，可以采用一维或三维热传导模型模拟烧蚀过程。一维烧蚀模型只考虑沿厚度方向的热传导，三维热传导模型则考虑沿周向网格单元与当前网格单元存在温差时所引起的热传导效应。与面向物体法类似，当某个单元的吸热总量达到完全熔化所需的热量后认为完全烧蚀，质量置零并改变局部几何外形。现有面向航天器法工程软件能够通过采用监视危险截面局部应力[4]或自定义物理量[18]的方式建立解体准则，一旦结构发生解体成两个或多个碎片，将分别计算碎片的再入过程。

2 国外软件

2.1 DAS

面向物体法工程软件DAS[1-2]由美国Lockheed公司于1998年开发，用于满足NASA 对航天器再入风险快速分析的需求。

DAS 中提供的航天器模型包括圆球、圆柱、立方体和平板，但只能是实心而不能是空心，需定义的参数包括物体形状、尺寸、质量和材料特性。DAS 的再入动力学模型采用三自由度弹道模型，烧蚀模型采用集总参数的零维热传导模型，因此不能模拟部分烧蚀效应以及解体。

DAS 的主要计算结果是再入物体完全烧蚀的消亡高度或对地面的毁伤面积，以表格形式显示。DAS 可用于航天器再入风险的初步分析，如果对其预测结果存在疑问，应采用更为精确的方法和工程软件作进一步计算和分析。

2.2 ORSAT

ORSAT 由NASA 约翰逊空间中心开发，是目前NASA 用于空间碎片再入分析的主要工具，也是面向物体法的工程软件。

与DAS 类似，ORSAT 的航天器模型也包括圆球、圆柱、立方体和平板，但可以模拟空心物体并提供总共10 种运动模式。ORSAT 的动力学模型采用三自由度弹道模型，烧蚀模型提供了零维热传导模型或考虑径向温度分布的一维热传导模型。ORSAT 采用高度准则判断是否解体，解体高度给定为78 km。

在连续流区，ORSAT 采用牛顿流模型计算物体的阻力系数，采用Detra-Kemp-Riddell 公式或Fay-Riddell 公式计算驻点热流从而得到平均热流。在过渡流区，ORSAT 采用正弦平方桥函数计算阻力系数，采用对数或Matting 桥函数计算气动热。此外，ORSAT 中还考虑了物体表面氧化热流效应。

ORSAT 已被NASA 用于许多航天器再入事件的预测分析以及标准算例验证中，比如用于与ESA的SCARAB 对比的空心圆球、德尔塔火箭第二级、钡燃料棒、SPARTAN 航天器以及UARS 航天器 等[3,32-34]。

2.3 SCARAB

ESA 的SCARAB 是目前唯一的面向航天器法工程软件，由德国宇航院 HTG（Hypersonic Technology Göttingen）中心于1995年开始开发。

如前所述，SCARAB 中航天器几何模型采用划分表面网格的三维模型，其对BeppoSAX 卫星的建模见图1[35]。由于气动模型能够提供航天器表面的压力分布，因此SCARAB 软件采用六自由度动力学模型，直接求解三个方向的平动和转动。该软件具有图形化操作界面，易于操作并且能够直观显示计算结果。采用一维或二维热传导模型得到结构内部的温度分布，并通过监视预先定义截面的局部 等效应力来判断结构在危险点 是否发生解体。

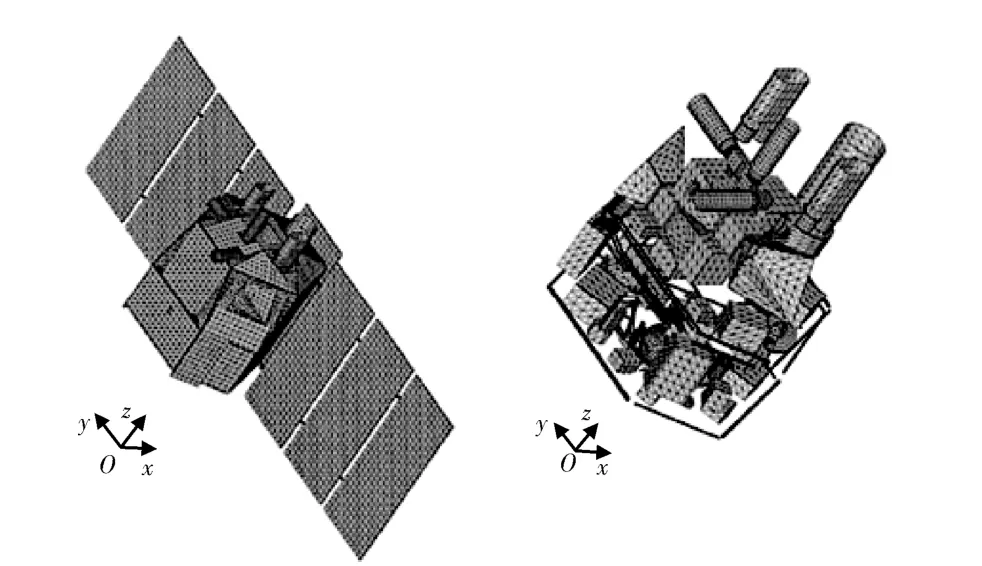
图1 SCARAB 对BeppoSAX 卫星的几何建模Fig.1 BeppoSAX satellite model by SCARAB

SCARAB 已被用于许多大型复杂航天器的再入预测问题，包括ATV、德国X 射线卫星ROSAT、阿里安娜5 火箭、意大利BeppoSAX 卫星以及Mir空间站等[35-37]。

2.4 其他软件

除了上述介绍的软件外，目前公开报道的航天器再入预测软件还有ESA 的DRAMA（Debris Risk Assessment and Mitigation Analysis）[38]、美国宇航公司（The Aerospace Corporation）的 AHaB（Atmospheric Heating and Breakup tool）[39]以及韩国的SAPAR（Survivability Analysis Program for Atmospheric Reentry）[40]等。

DRAMA 是欧洲空间碎片减缓标准（European Space Debris Mitigation Standard，ESDMS）的支持工具，其再入预测分析模块名为 SESAM（Spacecraft Entry Survival Analysis Module）。SESAM 采用与ORSAT 类似的模型和方法，但只采用零维热传导模型。AHaB 目前没有可获取的详细介绍资料。SAPAR 由韩国首尔国立大学开发，基于ORSAT 的模型和方法发展而来，主要区别是考虑了空心圆柱物体底部的辐射热损失效应，从而与德尔塔火箭第二级圆柱储箱再入观测结果符合得更好。

总的来说，目前基于面向物体法的航天器再入预测工程软件占绝大多数，而基于面向航天器法的仅有SCARAB。其原因一方面在于面向物体法软件易于实现且计算量小，而面向航天器法软件难于实现且计算量大；另一方面建模更加精细的面向航天器法并不一定比面向物体法更准确，因为前者所采用的预测模型仍然经过了很大简化，与实际情况相比存在差别。因此，计算量较小的面向物体法软件在工程应用中更受欢迎，而且通过不确定性分析能够在一定程度上给出模型近似所带来的影响，对工程实际也有重要指导意义。

3 国内软件

在国家国防科技工业局空间碎片专项资助下，清华大学与中国空间技术研究院合作开发了目前国内唯一一款面向物体法工程软件DRAPS。

3.1 DRAPS 简介

DRAPS 提供15 种航天器模型、51 种运动模式及其相应气动模型，从而能够对更多复杂外形的航天器再入进行模拟，其部分基本几何模型如图2所示。

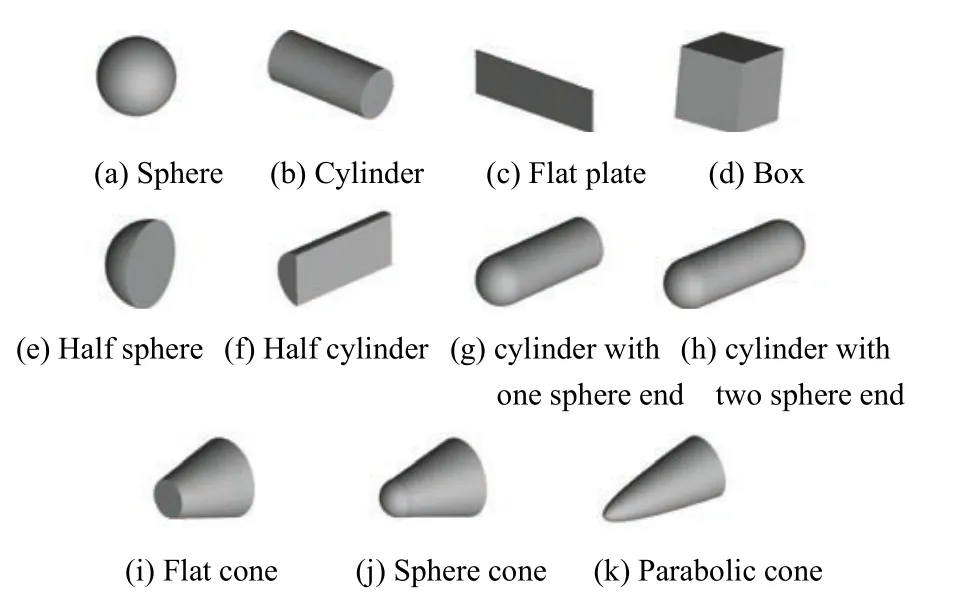
图2 DRAPS 中提供的基本几何模型Fig.2 The basic geometry models in DRAPS

DRAPS 的动力学模型采用三自由度弹道模型，烧蚀模型也采用零维热传导模型或考虑径向温度分布的一维热传导模型。其所采用的气动模型与ORSAT 类似，并通过CFD 和DSMC 模拟对部分气动模型进行了验证[5]。在解体模型方面，DRAPS除了高度准则外还提供温度准则、烧蚀准则（烧蚀到一定程度发生解体）和综合准则（达到上述任何一个解体条件就认为解体）。此外，DRAPS 中建立了多层嵌套碎片结构模型，能够模拟航天器部件间的包容关系。

DRAPS 的地面风险评估模型与ORSAT 相同，人口密度数据采用Columbia大学的2005年度地球人口密度分布数据，大气模型采用国际标准大气模型。

DRAPS 软件采用C++语言编写，GUI 界面通过Borland C++ 6.0 建立，其界面包括卫星碎片定义、初始状态、解体模型设置、轨道衰减仿真、再入结果与地面风险评估等。

3.2 典型仿真结果

目前DRAPS 已被用于多个简单或复杂外形航天器再入算例验证与测试[6]，包括标准空心圆球、德尔塔火箭第二级、SPARTAN 航天器、Intelsat VII-A 卫星、某航天器部分舱段等，通过对比DRAPS 与ORSAT 计算结果发现二者精度相近。

下面介绍采用DRAPS 对某典型航天器部分舱段再入仿真分析结果。该航天器内部分系统组成包括推进分系统、电源分系统、环控生保分系统、测控通信分系统、热控分系统和数管分系统，主要部件包括燃烧室、扩张喷嘴、推进剂储箱、气瓶、管路、阀门、辐射器、天线、配电器、数传设备、太阳电池板等共38 种。图3和图4给出了DRAPS对该航天器仿真得到的各部件再入轨迹、消亡高度以及落点位置。

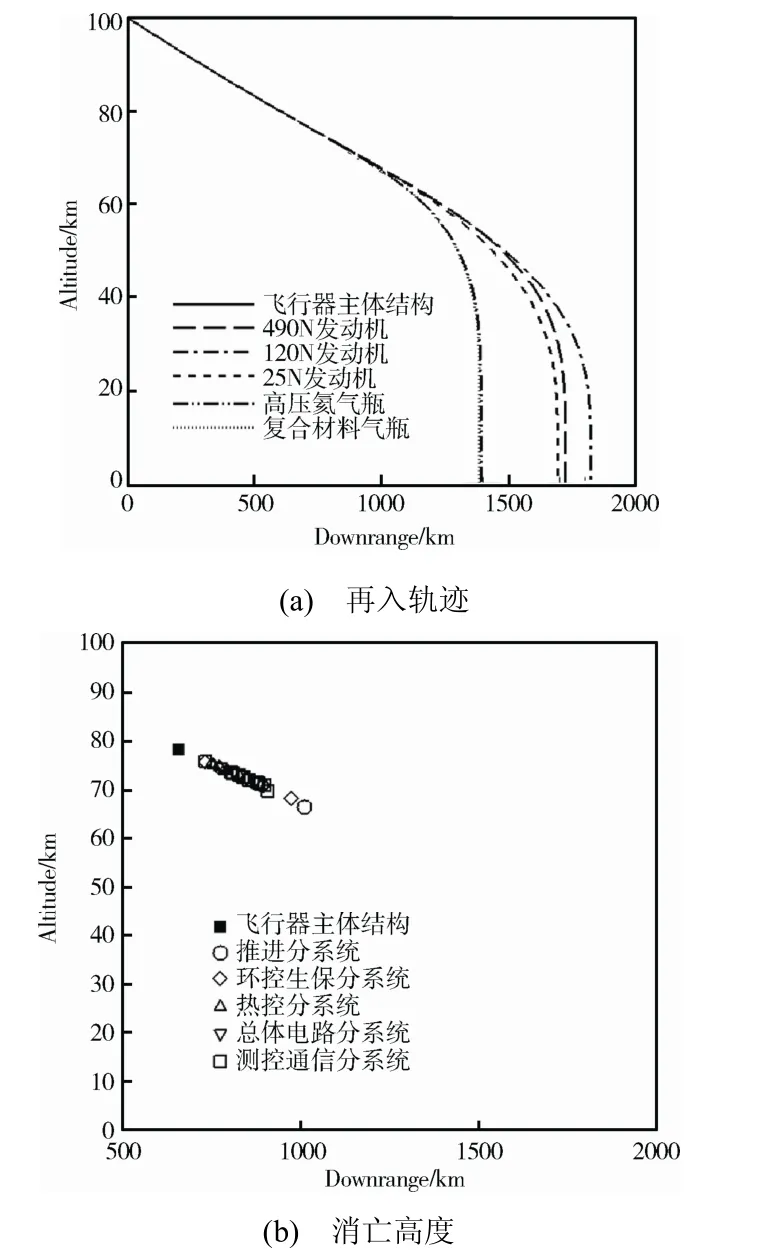
图3 DRAPS 对某航天器部分舱段再入仿真结果Fig.3 Reentry prediction results of certain spacecraft by DRAPS

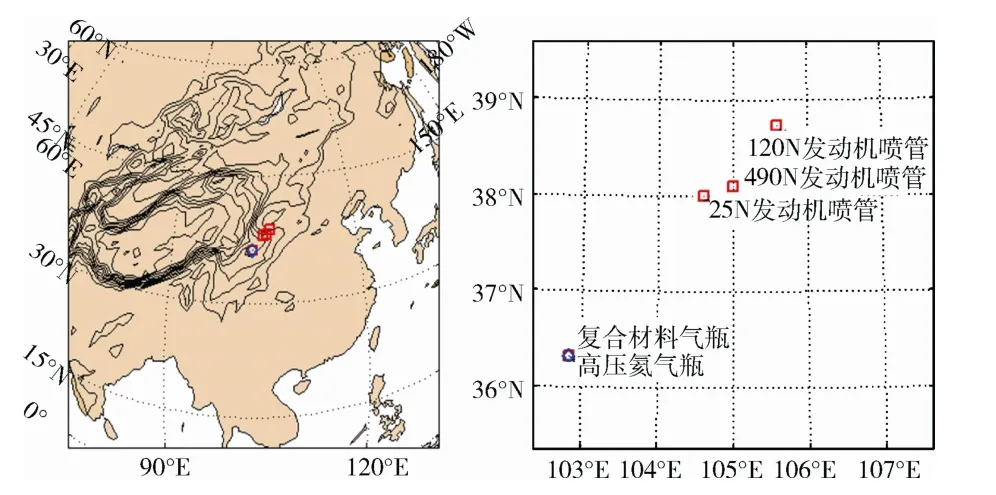
图4 DRAPS 对存活碎片落点仿真结果Fig.4 Landing locations of survived debris by DRAPS

3.3 下一步发展方向

尽管DRAPS 已具备航天器与空间碎片再入预测能力并与ORSAT 的预测精度相近，但还需在以下方面进一步改进与完善：

1）考虑更复杂的航天器外形。在航天器解体前采用面向航天器法模拟其再入过程，而解体后由于产生大量碎片，采用计算速度更快的面向物体法显然更合适。

2）采用更精确的气动模型。所采用气动力和气动热模型十分古老并经过很大简化，对其精度和适用性的验证还很不够；而随着计算手段的快速发展，利用精细流场仿真结果对气动模型进行校验和修正已成为可能。

3）设计更友好的用户界面。可采用目前流行的软件界面开发工具（如QT）对用户界面重新设计和美化，增加三维视景显示功能，虚拟再现航天器与空间碎片再入过程。

此外，还可采用更新的大气模型、地球人口密度分布模型等，以及建立航天器与空间碎片再入数据库等。

4 其他问题分析

4.1 碎片存活性

再入分析需要得到的一个重要结论是碎片能否存活至地球表面，这与再入物体的材料、几何形状、尺寸、质量等因素紧密相关。采用解析手段研究简单外形再入物体能够得到关于碎片存活规律的定性认识。

Koppenwallner 等[41]采用Allen-Eggers 弹道方程[42]以及Lees 驻点热流公式[13]研究实心圆球、圆柱和圆盘再入存活性问题。通过研究发现，碎片存活至地面源于两种机理：第一种是辐射，即当碎片表面热辐射能力足够强时，其温度始终低于熔点从而可以存活至地面；另一种是热容效应，即当物体容纳热量能力足够强时，高速气流的气动加热并不能使其完全烧蚀或熔化。Koppenwallner 等[41]给出不同材料以及不同外形碎片存活性随尺寸的变化，如图5所示。从图中可以看到，碎片在一定尺寸范围内才能存活。当d＜dmin，且碎片的面质比（A/m∝1/d）较小，再入速度较低，并且具有较强的辐射能力，从而能够存活至地面。当d＞dmax时，碎片的热容能力很强，从而能够存活至地面。图5上显示了实心圆球再入存活性随其直径及材料的变化关系。从中可以看出，钛质圆球具有最高的存活可能性，然后依次是不锈钢、镍铬合金和铜的，而具有低熔点和较差辐射特性的铝质圆球具有最低的再入存活性。图5(b)给出的是不同形状（圆球、圆柱、圆盘）钛金属碎片的再入存活性与其直径的关系。由于具有较小的面质比，圆盘的再入存活性最高，而在尺寸较大时圆球更容易存活至地面。Fritsche 等[43]在此基础上进一步研究了空心碎片（圆球、圆柱和立方体）再入的存活性问题，并得到与碎片尺寸和壁厚有关的存活和消亡区域（图6）。

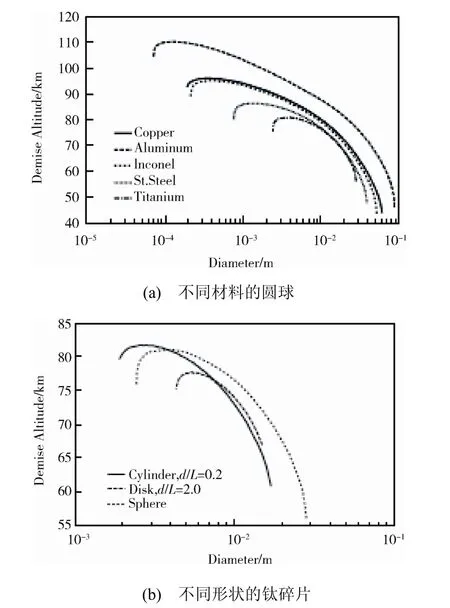
图5 碎片再入存活性与几何尺寸、材料的关系 Fig.5 Debris survivability versus size and material

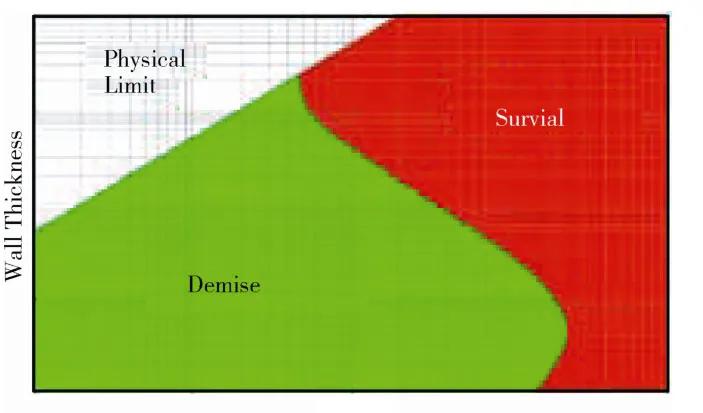
图6 空心碎片存活与消亡区域示意图Fig.6 Schematic diagrams for survival and demise regimes of hollow debris

通过上述研究可知，只有尺寸很小或很大的碎片能够存活至地面。小尺寸的存活碎片直径一般在1 mm 甚至更小，其对地面的影响可以忽略不计。工程中更关心的是大尺寸的再入存活碎片及其对地面的威胁程度。目前研究碎片存活性所考虑的因素只有碎片几何尺寸和壁厚，进一步可研究解体高度、再入角、方位角、运动模式对不同外形和材料碎片的存活性的影响，并形成数据库。

4.2 预测不确定性

尽管上述航天器再入预测方法均为确定性方 法，即给定相关参数和初始条件便能得到唯一确定的解，但是由于所采用的数学模型经过很多简化并包含许多不确定性因素，因此最终给出具有一定概率分布形式的预测结果应更为合理。

对于航天器在轨运动的长期预测，不确定性来源于轨迹追踪、航天器姿态、大气密度、太阳活动以及地磁场等。对于航天器从进入大气层至地球表面的再入预测，不确定性来源于再入初始条件（高度、速度、再入角等）、大气模型（大气参数、风场等）、气动模型（阻力系数、升力系数、气动热等）、解体高度等[5]，上述误差源的综合影响可能导致很大的再入碎片落点散布预测范围。

蒙特卡罗模拟法是考虑各个误差源对碎片落点影响的常用方法，如Rao 和Woeste[44]采用该法研究了卫星碎片的落点散布问题，并且该法已在返回舱再入落点散布估计中得到大量应用[45-48]。DRAPS 中提供对单个碎片再入落点散布范围进行计算的蒙特卡罗模拟功能[5]，并能给出落点散布椭圆形区域的长轴和短轴的3-σ值。

蒙特卡罗法的缺点是计算量太大，因此近年来人们致力于研究能够减小计算量的不确定性量化方法。Purcell 和 Barbery[49]采用温度协方差法（Temperature Covariance Method）研究了大气参数不确定性对再入落点散布的影响，获得与蒙特卡罗法相当的结果但计算量减小很多。Frank 等[50]采用一种概率模型方法研究了航天器再入解体不确定性对落点散布的影响。Reyhanoglu 和Alvarado[51]采用协方差传播法（Covariance Propagation Method）来估计存在解体时碎片再入落点散布范围。此外，近年来得到大量研究和应用的不确定性量化方法还包括多项式混沌法（Polynomial Chaos）[52-55]、响应面法（Response Surface Method）[56-57]、随机刘维尔方程（Stochastic Liouville Equation）[58]等。进一步研究可将上述方法应用到碎片再入落点散布的不确定性分析中来。

4.3 气动模型精度

无论面向物体法还是面向航天器法，目前所采用的气动力和气动热模型均基于大量假设和简化，并且面向物体法中对碎片运动模式的人为假定为气动力和气动热估算结果的可靠性带来很多质疑。因此，为获得气动估算的不确定性范围，对各种情况下、各种外形物体的气动力和气动热模型进行验证与校正十分必要。

本文作者利用CFD 和DSMC 方法对圆柱在自由分子流、过渡流和连续流中的气动力与气动热模型进行了初步验证研究[5]，图7是圆柱再入至不同高度处的流场数值计算结果并用于气动模型验证，其中H=30 km 流场通过CFD 方法计算得到，而H=110 km 和150 km 流场通过DSMC 方法计算得到。钝锥气动热估算结果见图8[59]。本文还研究了基于表面网格的高超声速气动力/热快速估算方法并开发了相应软件，对于典型外形，气动力和表面气动热的计算结果与实验结果以及CFD 结果吻合很好。进一步还需对各外形物体在不同马赫数、雷诺数、克努森数和姿态角条件下的气动模型进行更全面的验证研究。

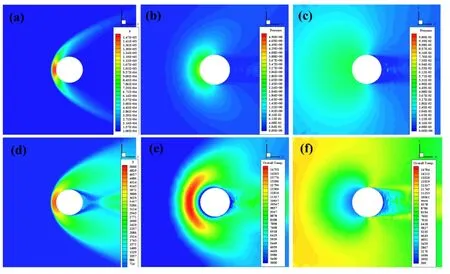
图7 圆柱再入流场计算结果：(a)～(c) H=30、110、150 km 的流场压力云图；(d)～(f) H=30、110、150 km 的流场 温度云图Fig.7 Numerical simulations of flow field for reentry cylinder∶(a)-(c) Pressure contours at H=30 km, 110 km and 150 km;(d)-(f) Temperature contours at H=30 km, 110 km and 150 km

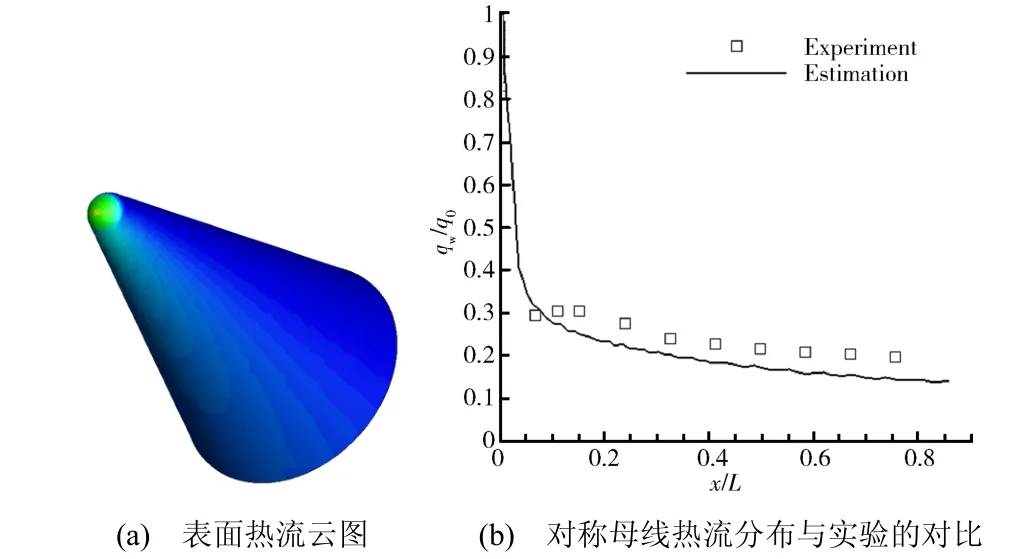
图8 钝锥气动热估算结果Fig.8 Aerodynamic heating estimation of a blunt cone

此外，在过去的半个世纪里，研究者们利用风洞实验、激波管实验或流场高精度数值模拟手段，对圆球、圆柱等简单外形物体在高速连续流或稀薄流中的气动问题开展了大量研究，并得到许多估算阻力系数的近似理论或经验关联式[60-66]。可充分利用已有研究数据来验证现有碎片气动模型。

5 结束语

随着人类航天活动的不断增多，航天器与碎片再入问题在国内外航天界受到越来越多的关注和重视。但由于其复杂性和多学科交叉性，相关研究和应用水平仍十分有限，一些基本问题尚未得到很好解决。在此背景下，本文对无控航天器与空间碎片再入问题工程预测方法与软件开发的研究现状进行了跟踪与总结，并讨论了若干关键问题和研究设想，希望能对此领域研究与工程应用起到抛砖引玉的作用。

（References）

[1]Reynolds R C, Soto A.Debris assessment software∶operators manual[G].NASA Johnson Space Center, 2001

[2]Opiela J N, Hillary E, Whitlock D O, et al.DAS user’s guide[G].Version 2.0.Orbital Debris Program Office, NASA Johnson Space Center.Houston, TX, 2007

[3]Bouslog S A, Ross B P, Madden C B.Space debris reentry risk analysis, AIAA 1994-591[R]

[4]Fritsche B, Klinkrad H, Kashkovsky A, et al.Spacecraft disintegration during uncontrolled atmospheric re-entry[J].Acta Astronaut, 2000, 47(2-9)∶513-522

[5]Wu Z N, Hu R F, Qu X, et al.Space debris reentry analysis methods and tools[J].Chin J Aeronaut, 2011, 24∶387-395

[6]胡锐锋, 吴子牛, 曲溪, 等.空间碎片再入烧蚀预测与地面安全评估软件系统[J].航空学报, 2011, 32(3)∶390-399 Hu Ruifeng, Wu Ziniu, Qu Xi, et al.Debris reentry and ablation prediction and ground risk assessment software system[J].Acta Aeronaut ET Astronaut Sinica, 2011, 32(3)∶390-399

[7]Lips T, Fritsche B.A comparison of commonly used re-entry analysis tools[J].Acta Astronaut, 2005, 57(2-8)∶312-323

[8]Tsien S H.Similarity laws of hypersonic flows[J].J Math Phys, 1946, 25∶105-106

[9]Bird G A.Molecular gas dynamics and the direct simulation of gas flows[M].New York∶Oxford University Press, 1994∶162-172

[10]Cercignani C.Rarefied gas dynamics[M].Cambridge∶Cambridge University Press, 2000∶1-30

[11]沈青.稀薄气体动力学[M].北京∶国防工业出版社, 2003∶141-156

[12]Anderson J D.Hypersonic and high temperature gas dynamics[M].New York∶McGraw-Hill Book Company, 1989∶45-75

[13]Lees L.Laminar heat transfer over blunted-nosed bodies at hypersonic flight speeds[J].Jet Propul, 1956, 26(4)∶259-269

[14]Fay J A, Riddell F R.Theory of stagnation point heat transfer in dissociated air[J].J Aeronaut Sci, 1958, 25(2)∶73-85

[15]Detra R W, Kemp N H, Riddell F R.Addendum to ‘Heat transfer to satellite vehicles re-entering the atmosphere’[J].Jet Propul, 1957, 27(12)∶1256-1257

[16]Cohen N B.Boundary-layer similar solutions and correlation equations for laminar heat-transfer distribution in equilibrium air at velocities up to 41,100 feet per second, NASA TR R-118[R], 1961

[17]Sutton K, Graves R A.A general stagnation-point convective- heating equation for arbitrary gas mixtures, NASA TR R-376[R], 1971

[18]Tewari A.Entry trajectory model with thermomechanical breakup[J].Journal of Spacecraft and Rockets, 2009, 46(2)∶299-306

[19]Dejarnette F R, Davis R M.A simplified method for calculating laminar heat transfer over bodies at an angle of attack, NASA TN D-4720[R], 1968

[20]Dejarnette F R, Hamilton H H.Inviscid surface streamlines and heat transfer on shuttle-type configurations[J].Journal of Spacecraft and Rockets, 1973, 10(5)∶314-321

[21]Hamilton H H, Dejarnette F R, Weilmuenster K J.Application of axisymmetric analog for calculating heating in three-dimensional flows[J].Journal of Spacecraft and Rockets, 1987, 24(4)∶296-302

[22]Hamilton H H, Greene F A, Dejarnette F R.Approximate method for calculating heating rates on three- dimensional vehicles[J].Journal of Spacecraft and Rockets, 1994, 31(3)∶345-354

[23]Hamilton H H, Weilmuenster K J, Dejarnette F R.Approximate method for computing laminar and turbulent convective heating on hypersonic vehicles using unstructured grids, AIAA 2009-4310[R]

[24]Wilmoth R G, Mitcheltree R A, Moss J N.Low-density aerodynamics of the stardust sample return capsule[J].Journal of Spacecraft and Rockets, 1999, 36(3)∶436-441

[25]Ivanov M S, Markelov G N, Gimelshein S F, et al.High-altitude capsule aerodynamics with real gas effects[J].Journal of Spacecraft and Rockets, 1998, 35(1)∶16-22

[26]徐姗姝.过渡区飞行器流场的数值模拟研究[D].北京∶清华大学, 2008

[27]Matting F W.Approximate bridging relations in the transitional regime between continuum and free- molecule flows[J].Journal of Spacecraft and Rockets, 1971, 8(1)∶35-40

[28]Nomura S.Correlation of hypersonic stagnation point heat transfer at low Reynolds number[J].AIAA Journal, 1983, 21(11)∶1598-1600

[29]Swaminathan P K, Taylor J C, Rault D F G, et al.Transition regime aerodynamic heating of missiles[J].Journal of Spacecraft and Rockets, 1996, 33(5)∶607-613

[30]Standard N S.Guidelines and assessment procedures for limiting orbital debris, NASA NSS 1995-1740[R]

[31]Baker R L, Weaver M.Orbital spacecraft reentry breakup[C]//50thInternational Astronautical Congress.Amsterdam, The Netherlands, 1999∶1-14

[32]Rochelle W M C, Kinsey R, Reid E, et al.Spacecraft orbital debris reentry aerothermal analysis[C]// Proceedings of the 8thAnnual Thermal and Fluids Analysis Workshop on Spacecraft Analysis and Design.Houston, TX, USA, 1997∶1-14

[33]Rochelle W C, Kirk B S, Ting B C, et al.Modeling of space debris reentry survivability and comparison of analytical methods[C]//50thInternational Astronautical Congress.Amsterdam, The Netherlands, 1999∶351-364

[34]Rochelle W C, Marichalar J J, Johnson N L.Analysis of reentry survivability of UARS spacecraft[J].Adv Space Res, 2004, 34(5)∶1049-1054

[35]Portelli C, Salotti L, Anselmo L, et al.BeppoSAX equatorial uncontrolled re-entry[J].Adv Space Res, 2004, 34(5)∶1029-1037

[36]Fritsche B, Koppenwallner G.Computation of destructive satellite re-entries[C]//Proceedings of the Third European Conference on Space Debris.Darmstadt, Germany, 2001∶527-532

[37]Fritsche B.Note on the application of SCARAB to the MIR re-entry[C]//Proceedings of the International Workshop MIR Deorbit.Darmstadt, Germany, 2001∶99-102

[38]Klinkrad H, Fritsche B, Lips T.A standardized method for re-entry risk evaluation[C]//55thInternational Astronautical Congress.Vancouver, Canada, 2004∶141-155

[39]The Aerospace Corporation.Atmospheric heating and breakup (AHaB) tool[G]

[40]Sim H S, Kim K H.Reentry survival analysis of tumbling metallic hollow cylinder[J].Adv Space Res, 2011, 48∶914-922

[41]Koppenwallner G, Fritsche B, Lips T.Survivability and ground risk potential of screws and bolts of disintegrating spacecraft during uncontrolled re-entry[C]// Proceedings of the Third European Conference on Space Debris.Darmstadt, Germany, 2001∶533-539

[42]Allen H J, Eggers A J.A study of the motion and aerodynamic heating of missiles entering the Earth’s atmosphere at high supersonic speeds, NACA R-1381[R], 1957

[43]Fritsche B, Lips T, Koppenwaller G.Analytical and numerical re-entry analysis of simple-shaped objects[J].Acta Astronaut, 2007, 60(8/9)∶737-751

[44]Rao P P, Woeste M A.Monte Carlo analysis of satellite debris footprint dispersion, AIAA 1979-1628[R]

[45]Spencer D A, Braun R D.Mars Pathfinder atmospheric entry∶trajectory design and dispersion analysis[J].Journal of Spacecraft and Rockets, 1996, 33(5)∶670-676

[46]Desai N P, Braun R D, Powell R W, et al.Six- degree-of-freedom entry dispersion analysis for the METEOR recovery capsule[J].Journal of Spacecraft and Rockets, 1997, 34(3)∶334-340

[47]Queen E M, Cheatwood F M, Powell R W, et al.Mars polar lander aerothermodynamic and entry dispersion analysis[J].Journal of Spacecraft and Rockets, 1999, 36(3)∶421-428

[48]Desai N P, Cheatwood F M.Entry dispersion analysis for the Genesis Sample Return Capsule[J].Journal of Spacecraft and Rockets, 2001, 38(3)∶345-350

[49]Purcell E W, Barbery T B.Dispersions resulting from atmospheric variations[J].Journal of Spacecraft and Rockets, 1968, 5(8)∶1005-1007

[50]Frank M V, Weaver M A, Baker R L.A probabilistic paradigm for spacecraft random reentry disassembly[J].Reliab Eng Syst Saf, 2005, 90∶148-161

[51]Reyhanoglu M, Alvarado J.Estimation of debris dispersion due to a space vehicle breakup during reentry[J].Acta Astronaut, 2013, 86∶211-218

[52]Wiener N.The homogeneous chaos[J].Am J Math, 1938, 60(4)∶897-936

[53]Eldred M S.Recent advances in non-intrusive polynomial chaos and stochastic collocation methods for uncertainty analysis and design, AIAA 2009-2274[R]

[54]Sahai T, Pasini J M.Uncertainty quantification in hybrid dynamic systems[J].J Comput Phys, 2013, 237∶411-427

[55]Luchtenburg D M, Brunton S L, Rowley C W.Long- time uncertainty propagation using generalized polynomial chaos and flow map composition[J].J Comput Phys, 2014, 274∶783-802

[56]Myers R H, Montgomery D C, Anderson-Cook C M.Response surface methodology∶process and product optimization using designed experiments[M].Hoboken, NJ∶John Wiley &Sons, 2009∶1-680

[57]Riley M E, Grandhi R V.Quantification of modeling- induced uncertainties in simulation-based analyses[J].AIAA Journal, 2014, 52(1)∶195-202

[58]Halder A, Bhattacharya R.Dispersion analysis in hypersonic flight during planetary entry using stochastic Liouville equation[J].J Guide Control Dyn, 2011, 34(2)∶459-474

[59]胡锐锋.高速飞行气动环境、气动特性快速预测与应用[D].北京∶清华大学, 2013

[60]Kinslow M, Potter J L.Drag of spheres in rarefied hypervelocity flow[J].AIAA Journal, 1963, 1(11)∶2467-2473

[61]Bailey A B, Hiatt J.Sphere drag coefficients for a broad range of Mach and Reynolds numbers[J].AIAA Journal, 1972, 10(11)∶1436-1440

[62]Henderson C B.Drag coefficients of spheres in continuum and rarefied flows[J].AIAA Journal, 1976, 14(6)∶707-708

[63]Loth E.Compressibility and rarefaction effects on drag of a spherical particle[J].AIAA Journal, 2008, 46(9)∶2219-2228

[64]Klett R D.Drag coefficients and heating ratios for right circular cylinders in free-molecular and continuum flow from Mach 10 to 30, SC-RR-1964-2141[R].Sandia Corp, Albuquerque, NM

[65]Randall D E.Method for estimating the drag coefficient of a tumbling circular cylinder, SC-TM-1964-0528[R].Sandia Corp, Albuquerque, NM

[66]Lutz S A.Heating correlations for bluff cylinder hypersonic rarefied flows, AIAA 2003-4060[R]