基于能量检测法的统计特性分析*
王 懋,袁新波,张海黎
(1.电子工程学院,安徽 合肥230037;2.国营990厂,安徽 合肥230037;3.北京地区军事代表室,北京100083)
0 引言
目前较为通用的信号检测方法主要有能量检测法、匹配滤波器法、循环平稳特征检测法和高阶累积量法等[1-8]。其中能量检测法是一种在没有任何先验知识的情况下判断未知信号有无的最简单、直接和有效的信号检测方法,是利用了信号加噪声的能量应大于噪声的能量的原理。由于能量检测方法对信号没有作任何假设,因此是一种盲检测算法,应用范围广泛。例如在认知无线电领域,需要对空闲频谱资源进行检测,能量检测法是一种基础的频谱感知方法[7];在超宽带无线通信领域,能量检测法被应用于超宽带接收机,解决时间同步、TOA 估计问题等[8-10]。然而关于能量检测法中的检测量统计特性分析以及检测门限选择问题,目前一直缺少深入的分析及验证,使得能量检测器的应用及性能分析受到一定限制[9-13]。
因此,本文针对能量检测器的检测量统计特性进行了分析,包括对仅有噪声情况和信号加噪声情况下能量检测结果统计特性的分析,为能量检测法的应用提供理论支持。
1 能量检测法
信号检测问题,即根据接收到的混合波形(信号加噪声,或噪声),作出有无信号存在的判决。电磁信号在传输信息的过程中会遇到各种干扰,其中最常见的噪声干扰是随机过程,此外,有用信号也常呈现随机性。因此,信号检测问题可以用如图1所示的统计接收原理框图来描述。
接收机输入端的有用信号用 ()s t 表示,噪声干扰用 ()n t 表示。信号 ()s t 随发射机是否发射而或有或无,而噪声 ()n t 却始终存在。因而接收机的输入有两种可能情况:1)当发射信号时,输入为信号加噪声,即X (t )=s (t )+n (t) ;2)当不发射信号时,输入仅有噪声,即 ()X t = ()n t 。高频信号 ()X t 经接收机处理后,解调成低频信号 ()Y t ,送到检测设备去作有无信号的判决。由于接收机的输出 ()Y t 同样具有上述两种可能情况,故需判决在 ()Y t 中是否含有信号。
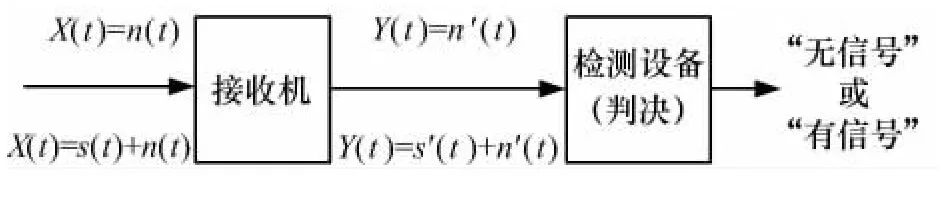
图1 信号检测统计接收原理框图
能量检测方法利用信号加噪声的能量总是大于噪声的能量的自然规律,首先获取一定频带范围内的接收信号,然后再对信号作能量积累,如果积累的能量高于一定门限,则说明有信号存在,如果低于一定门限,则说明仅有噪声。假设有用信号为窄带信号,则能量检测器的原理框图如图2所示。

图2 能量检测器原理框图
窄带正态过程 ()Y t 经过平方律检波器作包络检波,取得包络过程R2(t) ,对其乘以1/σ2作归一化,再对它作n 次独立取样,然后用加法器将它们相加(积累)后输出,去作统计判决。脉冲雷达就常用这种检测方法,其回波信号经检波后为一串视频窄脉冲,如果采用隔周期(雷达脉冲重复周期)进行取样,在所得的独立取样中,可能全无信号而仅有噪声,也可能噪声中混有信号,因而只要把它与门限电平作比较,即可判别出有无信号存在。
2 统计特性分析
为了方便分析,假设经过窄带滤波器后的窄带噪声 n(t)是均值为零、方差为σ2的平稳正态过程,其表示式为:
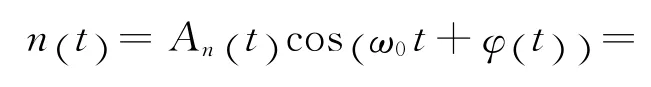

式中,An(t) 为包络,φ(t) 为相位,ω0为载波频率,nc(t) 和ns(t)分别为同相和正交分量。因此,nc(t) 和ns(t) 仍为平稳正态过程,且均值为零、方差仍为σ2,由于同一时刻的两个正交分量nc(t) 与ns(t) 不相关,故对正态过程来说,也就统计独立。
设信号为随机初相信号:

式中,振幅A 和角频率ω0均已知,而相位θ在上均匀分布。
通过带通滤波器后的信号与噪声合成过程为:

令:

则:
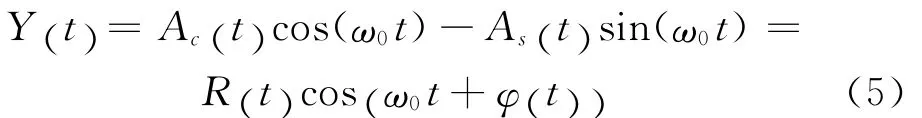
若无信号,则分量nc(t) 和ns(t) 都是零均值、方差为σ2的正态随机变量,且统计独立。若有信号时,只要随机变量θ给定,则Acosθ和Asinθ也就确定,故由Ac(t) 和As(t) 的 表 达 式 可 知,分 量Ac(t) 和As(t) 仍为正态随机变量,且仍统计独立。
根据以上分析,并结合能量检测器的原理可知,窄带正态过程 ()Y t 经过平方律检波器作包络检波,取得包络的过程为。由于无论有无信号,Ac(t) 和As(t) 均呈正态分布,这两个低频(视频)过程乘以1/σ2作归一化,再分别作n 次独立取样,取得2n个统计独立的标准正态随机变量(Ac和As)之平方,然后用加法器将它们相加(积累)后输出v,显然随机过程v 将服从χ2分布或非中心χ2分布。下面将按照噪声输入和信号加噪声输入两种情况分别进行详细分析。
2.1 只有噪声输入时
当只有噪声输入时,通过令式(4)中的A=0,即可得:

根据前面对式(1)中nc(t) 和ns(t) 统计特性的分析结果可知,它们分别服从均值为0、方差为σ2的正态分 布,即nc(t) ~N (0 ,σ2),ns(t) ~N (0 ,σ2),而且两者相互统计独立。
根据能量检测器的实现原理,当对归一化后的包络平方进行n次独立采样并累加求和后,检测量v 可表示为:
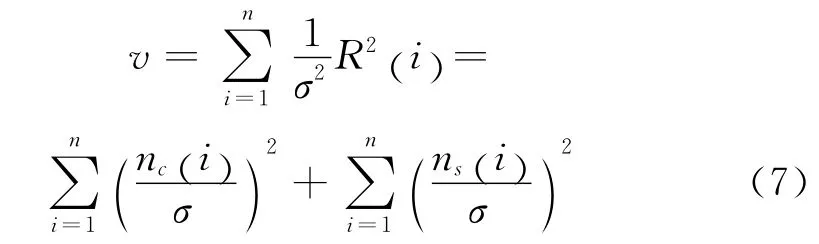
根据前面的分析可知:

故根据χ2分布的定义式可得,检测量v服从自由度为2n的χ2分布,即:

进一步得,只有噪声输入时,检测量v的概率密度函数为:

2.2 信号加噪声输入时
与前面分析相类似,利用式(4),当信号加噪声输入时:

即Ac(t) 和As(t) 分别服从均值为Acosθ 和Asinθ,方差均为σ2的正态分布。
此时检测量v可表示为:

由于:

根据前面的分析结果式(8),可以看出(1/σ) Ac(i) 和 (1/σ) As(i) 分别由标准正态分布和常数相加而成,即式(12)可以改写为:

根据非中心χ2分布的定义式可得,此时检测量v服从自由度为2n的非中心χ2分布,即:

故可得信号加噪声输入时,检测量v 的概率密度函数为:


3 仿真分析
3.1 信噪比与累积时间对检验量统计特性的影响分析
根据能量检测法的实现原理,分别对H0假设(输入仅为噪声情况)和H1假设(输入为信号加噪声情况)进行仿真。从前面的分析可知,仅有噪声输入时的检验统计量服从χ2分布,信号加噪声输入的检验量服从非中心χ2分布,故根据式(10)和式(17)的概率密度表达式,可得相应统计检测量的概率密度曲线。其中概率密度随信噪比SNR 和累积时间n 的变化曲线分别如图3和图4所示。

图3 概率密度随信噪比SNR 的变化曲线(n=18)
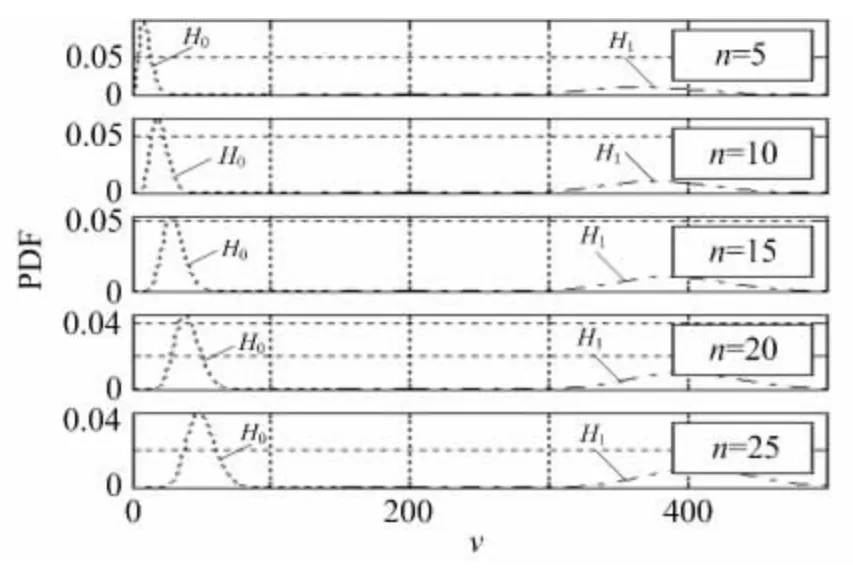
图4 概率密度随累积时间n的变化曲线(SNR=10dB)
图3给出了累积时间一定(n=18),概率密度曲线相对于信噪比SNR 的变化曲线。从图中可以看出,随着信噪比的增大,H1假设的概率密度曲线中心逐渐向右平移,即逐渐远离H0所对应的概率密度曲线,且信噪比越大,偏离越远。该仿真结果表明,信噪比越大能量检测法的性能越好。
图4给出了信噪比一定(SNR=10dB),概率密度曲线相对于累积时间n 的变化曲线。从图中可以看出,随着累积时间的增大,H0假设和H1假设的概率密度曲线分离越来越远,H1假设的概率密度曲线峰值越来越大,即表示累积时间越长越有利于信号存在性的检测。
3.2 不同检测门限对检测性能的影响分析
为了分析不同检测门限对能量检测法统计特性分析的正确性及其检测性能的影响,仿真中选择如下三种门限,即:

式中,Th1 为只有噪声输入时的检测量统计均值,Th3为信号加噪声输入时的检测量统计均值,而Th2为噪声和信号加噪声输入时检测量的均值。其中检测门限随信噪比和累积时间的变化曲线分别如图5和图6所示,通过比较可知,Th2是比较理想的门限取值,而Th1和Th3略次于该门限值。

图5 检测概率Pd 随信噪比SNR 的变化曲线(n=18)
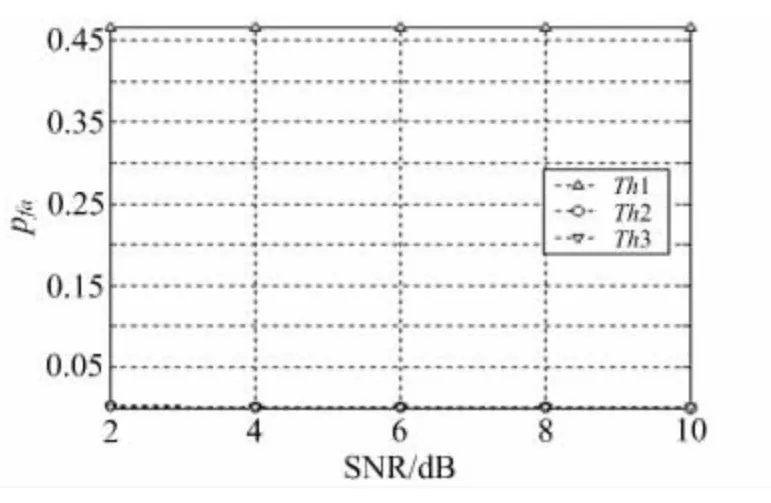
图6 虚警概率Pfa随信噪比SNR 的变化曲线(n=18)
为了方便,定义信噪比为SNRi=0.5A2/σ2。检测概率Pd和虚警概率Pfa相对于累积时间的变化分别如图7和图8所示。
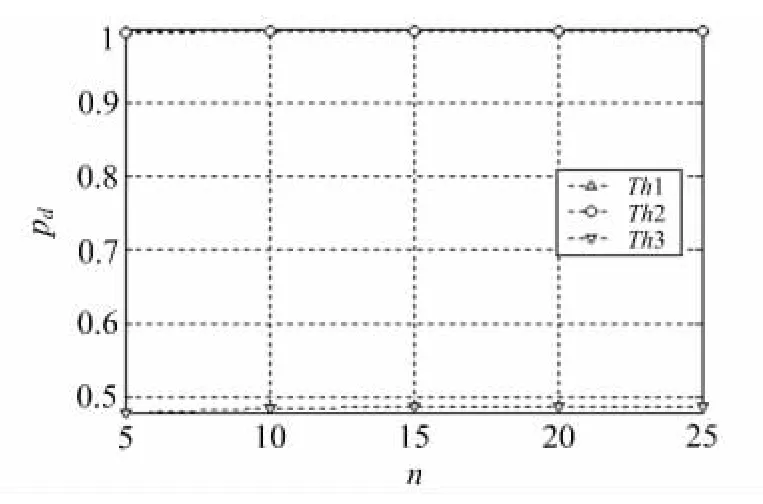
图7 检测概率Pd 随累积时间n 的变化曲线(SNR=10dB)
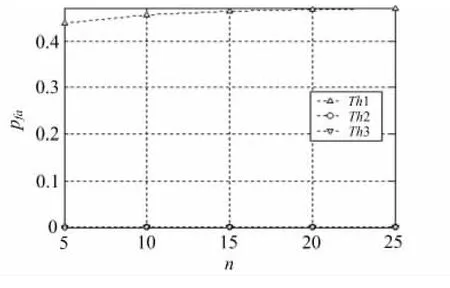
图8 虚警概率Pfa随累积时间n 的变化曲线(SNR=10dB)
可以看出,Th1 对应的检测概率较高较好,虚警概率较高较差;Th3 对应的检测概率较低较差,虚警概率较低较好;Th2 对应的检测概率较高较好,虚警概率也比较低。通过以上仿真分析可以看出,本文推导的统计特性是正确的。
4 结束语
能量检测法是一种在没有任何先验知识的情况下判断未知信号有无的最简单、直接和有效的信号检测方法。本文通过对能量检测法的统计特性进行系统分析和理论推导,发现能量检测输出结果在只有噪声输入的情况下服从卡平方分布,在信号加噪声输入的情况下服从非中心卡平方分布,并利用仿真验证了本文推导的正确性,为能量检测法的应用提供了参考和依据。■
[1]Fillatre L.Constrained epsilon-minimax test for sim-ultaneous detection and classification[J].IEEE Trans.on information theory,2011,57(12):8055-8071.
[2]Wang Pu,Li Hongbin,Djurovic I,et al.Integrated cubic phase function for linear FM signal analysis[J].IEEE Trans.on Aerospace and Electronic Systems,2010,46(3):963-977.
[3]Zivanovic M,Schoukens J.On the polynomial approximation for time-variant harmonic signal modeling[J].IEEE Trans.on Audio,Speech,and Language Processing,2010,19(3):458-467.
[4]Meng XW.Performance analysis of ordered-statistic greatest of-constant false alarm rate with binary integration for M-sweeps[J].IET Radar Sonar Navig.,2010,4(1):37-48.
[5]Luo Zhiquan,Ma Wingkin,Man-choso A,et al.Semidefinite relaxation of quadratic optimization problems[J].IEEE Signal Processing Magazine,2010,27(3):20-34.
[6]Chen W,Xu X,Wen S,et al.Super-resolution direction finding with far-separated subarrays using virtual array elements[J].IET Radar Sonar Navig.,2011,5(8):824-834.
[7]沈雷,王海泉,赵知劲,等.认知无线电中基于拟合优度的频谱盲检测算法研究[J].通信学报,2011,32(11):27-34.
[8]Wang Feng,Tian Zhi,Sadler BM.Weighted energy detection for noncoherent ultra-wideband receiver design[J].IEEE Trans.on Wireless Communications,2011,10(2):710-720.
[9]杨志华,张钦宇,王野.非相干能量检测UWB接收机误码率性能优化[J].电子学报,2009,37(5):951-956.
[10]姜向远,张焕水,王伟,等.IR-UWB能量检测接收机中基于门限的TOA 估计[J].电子与信息学报,2011,33(6):1361-1366.
[11]刘义贤,季飞,余华.认知无线电网络中基于噪声功率估计的能量检测性能[J].电子与信息学报,2011,33(6):1487-1491.
[12]晋本周,张盛,程永生,等.基于超宽带能量检测方案的数字脉冲间隔调制[J].系统工程与电子技术,2011,33(9):2096-2100.
[13]李国君,赵栋华.无源双基地雷达动目标快速检测算法[J].雷达科学与技术,2013,11(2):145-149.

