湍流理论研究进展简介

葛均建

（郑州大学，河南 郑州 450000）

湍流行为的有限维非线性动力系统的渐近解接近不规则性，但是存在较大困难的是，从理论上把有限维非线性动力系统理论推广到属于无限维非线性动力系统的偏微分方程的初边值问题。但是在湍流研究的实践中，在大雷诺数的情况下，N-S方程的初边值问题，渐近解的不规则性。其中一个证据是利用近代先进的计算机来数值求解N-S方程的实验。在一些简单几何边界流动的数值实验中，不规则解在时间、空间上得以模拟，并且可以得到由这些解的系综统计或时间平均中得到和物理实验相同的统计结果，其次一个证据是Lorenz的奇怪吸引子解，在N-S方程有限维近似解中发现，当雷诺数很大时，方程存在长时间的不规则振荡解，这种解被称为奇怪吸引子，正是Lorenz的研究才开启了近代混沌理论研究的先河。

一、研究进展及启示

在湍流理论中，Reynolds提出了两个理论，一个理论是把流动变成脉动部分和平均部分，另一个理论是流动状态稳定性的判断依据[1]。

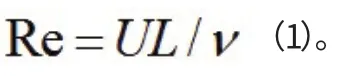
第二个理论的判断依据是：

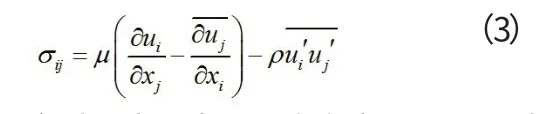
在湍流理论的研究过程中，出现了许多常见问题：对于具有变化物理特性的系统，如何确定（3）中的物理参量；在层流流动中存在有稳定性问题，不可压缩流体运动在确定临界雷诺数的过程中表现出来的不确定性问题，层流转变成湍流的原理问题，这是由于该不可压缩流体存在着一个变换区域，该变换区域是稳定的层流变换成表征掺混现象的平稳湍流；由于出现表观湍流应力张量的分量导致雷诺方程的不封闭问题，有关的效应在湍流扰动的影响下出现同介质物理性质脉动；导电介质的湍流与电磁场之间的相互影响；在湍流流动的边界条件上，尤其是拥有一定的边界上，在距离固定壁面不远处存在有层流区间，该区间的下边界条件为流体附着在固定壁面上，而把湍流能量达到最大值作为其上边界条件。能量耗散作为湍流热量的原理，出现在湍流非均匀性的最小的线性尺度（4）上；用湍流Prandtl数（5）来描述的能量、冲量和掺入物质的湍流输运之间的关系；对湍流影响的某些添加物；在非均匀介质中，尤其是气液混合物的稳定性和湍流问题；在非牛顿流体中，流动的介质的湍流的发展体现出的物理特性等等。

在Reynolds的文章中，他提出利用能量来计算（1）的临界雷诺值，然后，H.Lorentz.V.Orr等人对该研究进行了继续发展。在T.Karman的著作中，他总结了有关这方面的努力，可是他的这种总结阻碍了该方向的继续发展。研究已经表明，实验确定的临界雷诺数比稳定性的能量判据要大很多。在30年代，他指明了存在固有的雷诺数的研究方向，并且总结了湍流边界粘性底层的尺寸。这种观点最近还在继续发展。

湍流理论由于雷诺方程的不封闭性问题产生了两个基本方向。首先一个方向是湍流的统计描述概念，该概念由Friedmann，E.Burgers和Keller提出；其次一个方向是半经验唯象理论，Prandtl，Taylor， Konmoropon等的文章与此概念的卓有成果的研究和产生有关。

均匀各向同性湍流的准相似条件以及相应均匀各向同性湍流的涡旋结构统计理论由周培源等提出，该理论得到实验的验证[2]，进一步，在一般的剪切湍流中，均匀各向同性湍流中得到的准相似条件得到了推广，然后，假定关联方程的耗散项，湍流的统计理论使用逐级近似方法得到了发展[3]，经实验验证所得结果符合实际。在文[4]中， 湍流平均运动方程和脉动速度关联方程利用逐级迭代法进行求解，高阶脉动关联函数在以往求解时须联立一系列不同阶脉动速度关联方程求解所带来的方程不封闭性问题得到了完美解决[5]。

[1]С.С.Кутателадэе,董务民等. 湍流理论基本思想发展.力学进展,1981(4).

[2]周培源等. 不可压缩流体的湍流理论, 中国科学( A) , 1987 ( 4) :369 ～380.

[3]魏中磊等. 网格湍流微结构的实验研究. 力学学报, 1988, 20 ( 3) :200 ～205.

[4]林建忠等. 求解脉动速度关联函数的新方法及其在平面湍尾流中的应用. 力学学报, 1993, 25( 6) : 643 ～650.

[5]周培源. 湍流理论的近代发展[J]. 物理学报. 1957(03).