基于DIgSILENT数据接口DGS的含风电电力系统随机潮流分析
孙雯,戎晓雪,别朝红,石文辉,柯丹
(1. 西安交通大学 电力设备电气绝缘国家重点实验室,陕西 西安 710049;2. 国网山东省电力公司 济南
供电公司,山东 济南 250012;3. 中国电力科学研究院,北京 100192)
目前石油、煤炭等传统化石能源日益枯竭,新能源以其清洁、可再生等优点得到不断发展[1-2]。由于风能资源丰富且风力发电技术日趋成熟,风电并网规模日益增大。受自然界气候的影响,风电出力具有随机性、波动性和间歇性等特点。当电力系统中的风电场数目较多时,利用传统的确定性潮流分析系统状态不仅计算量巨大而且无法全面反应系统的运行情况。而随机潮流可以在考虑各种随机因素的同时,概率地统计出电力系统稳态运行情况,得到更为全面的系统运行指标[3-6]。
目前已有学者对含风电电力系统随机潮流进行分析研究。但多数文献只是将各风电场的风速看作独立变量进行计算[7-10],并没有考虑到处于同一风区、地理位置相近的多个风电场风速之间较强的相关性[11-12],不能准确地评估电力系统的运行风险。文献[13-14]提出一种可以处理多个输入随机变量相关性的基于拉丁超立方采样的Monte Carlo随机潮流计算方法,较传统的Monte Carlo模拟法的效率有所提高,但仍需要进行大量的仿真计算,耗时较长。文献[15]提出一种基于Cholesky分解的计及输入变量相关性的半不变量随机潮流计算方法,但其对具有相关性的输入变量处理方法较为复杂,在求取半不变量时仍利用的Monte Carlo抽样,且要求已知输入变量的边际累积分布函数和相关系数矩阵,计算量较大。文献[16]采用Copula函数建立多风电场的风速相关性模型的过程中,利用最大似然估计法得到Copula参数,在得到具有相关风速样本时已产生相应的误差。
以上方法均不能快速地求解考虑风电场相关性时的电力系统随机潮流,且未考虑风速波动较大导致的线性化潮流不适用问题[17]。另一方面,常用随机潮流算法多是以IEEE标准数据格式为输入,而我国电力系统常用DIgSILENT软件进行分析,电网网架的数据格式为DIgSILENT数据格式DGS,由于输入文件的不匹配导致计算效率的大大降低。针对以上问题,本文首先将各风电场的风速及出力离散化,建立考虑风电场相关性的离散化联合概率分布模型,逐个判断离散点是否符合线性化潮流方程,并结合半不变量和Gram-Charlier级数展开方法进行随机潮流评估计算[18]。其次,因DIgSILENT软件具有丰富的元件库和灵活的自定义模型,常以此为平台搭建各地区电力系统仿真模型,故本文研究了基于DIgSILENT软件的DGS数据接口技术,使含风电电力系统随机潮流算法在实际电力系统得到应用推广,具有较好的工程应用价值。
1 考虑风速相关性的风电场出力模型
1.1 单个风电场出力离散化
在风力发电地区,风速一般具有昼夜分布特性,波动性非常大。当风电场装机容量较大时,风电场出力的变化范围随之变大。当风电场出力波动达到一定程度时,则不能使用线性化潮流方法计算潮流,否则将导致较大的误差。由此,本文将风电场的出力离散化,逐个判断各离散点是否满足线性化潮流的适用条件。
以有功出力为例,假设风机出力在0到额定值Pr之间波动时,根据风电出力波动范围和电网规模选取风机出力离散段数为h,则Pstep=Pr/h为每一段有功出力间隔,取每一段出力的期望值为对应的离散点:

若已知风电场有功出力的概率密度函数为f(P),则每个离散点对应的概率为

当风电场有功出力为离散概率密度函数时,则各离散点的概率值为

其中:i=1,2,3,…,h。
本文采用恒功率控制的双馈感应式发电机,基于监测的历史风速数据,根据风速-功率特性曲线计算出风电场的有功出力和无功出力,并逐个判断该出力值属于哪个离散点范围,则相应的离散点概数加1。其中,当风机有功出力为0时,取离散点Pw0=0,其离散概率为

当风机有功出力为额定功率Pr时,取离散点Pw(h+1)=Pr,其离散概率为
故得到每个风电场出力有h+2个离散点数。
1.2 单个风电场出力离散化
当同一风区分布多个风电场时,本文通过建立多个风电场之间出力的离散化联合概率分布,来表征各相邻风电场之间风速的相关性关系,建立过程如图1所示。
1)读取m个具有相关性风电场的k组历史风速数据。
2)依据风速-功率特性曲线,将风速转化成风机出力。
3)设定离散点数N,分别将每个风电场出力离散化,得到各离散点有功和无功出力值(Pw1,Qw1)到(PwN,QwN),可以得到多个风电场联合概率分布中各离散点出力(Pwi1,wi2,…,wij,…,wim,Qwi1,wi2,…,wij,…,wim),i=1,2,…,Nm;j=1,2,…,m;ij=1,2,…,N。
4)分析第a组出力数据中第b个风电场出力值属于哪个离散点,则相应离散点的概数加1。
5)判断是否处理完a组数据中所有风电场出力值。若b 图1 风电出力离散化联合概率分布建立流程Fig. 1 Calculation flow chart of Joint discrete probabilistic model of wind power 6)判断是否处理完k组风电场出力。若a 7)处理完所有出力数据,将每个离散点处的概数除以k,得到联合概率分布中各离散点处的概率值pi1,i2,…,ij,…,im。 表1以两个风电场为例建立风电出力的离散化联合概率分布模型。 表1 两风电场出力的离散化联合概率分布Tab. 1 Joint discrete probabilistic model of windpower 电力系统潮流方程如下: 式中,W为节点注入功率,包括有功和无功功率;X为节点的状态变量,包括各节点的电压负值和角度;Z为支路潮流随机变量;f和g分别为系统潮流方程和支路功率方程。 当节点注入功率的变化较小时,可使用传统的基于半不变量法的随机潮流分析算法,即在基准运行点处利用泰勒级数展开并忽略高次项,由此得到各节点电压和支路潮流的变化量与节点注入量的变化量关系为 式中,ΔW为节点注入功率向量的变化量;ΔX为节点电压状态变量的变化量;J0为牛顿法最后一次迭代所用的雅可比矩阵;ΔZ为支路功率向量的变化量;G0为支路功率对节点电压求一阶偏导数所得矩阵。 由于风电场出力的波动性较强,当风电场出力的变化量较大时,忽略泰勒展示的高次项将带来较大的误差,因此利用式(7)表示的线性化潮流方程求取节点电压和支路功率的变化量也将会有较大的误差。为了减少这一误差,本文引入线性化潮流方程的适用判据,设置潮流方程线性化的阈值ΔCf,逐点判断1.2中建立的多风电场的出力离散化联合概率分布模型中概率大于0的离散点是否适用线性化潮流方程,如果适用,则可根据式(7)求取风电场出力由额定功率变为某离散点时,系统节点电压和支路潮流的变化量;否则需要重新计算潮流来确定系统各节点电压和支路功率的变化量。 以m个风电场分别接入m个节点上为例,某一时刻各风电场的风速从额定vr风速变化成风速v1、v2、…、vm,各风电场的出力将由额定出力(Pr,Qr)变为(PW1,QW1)、(PW2,QW2)、…、(PWm,QWm)。则接入风机的节点有功和无功注入功率的变化量分别为 式中,ΔPwi和ΔQwi分别为接入风机节点有功和无功注入功率的变化量。 其余非风机接入节点的注入功率变化量为0。设系统有n个节点,l条支路。依据式(7)计算出各节点状态变量和支路功率向量的变化量分别为式中,Δθj、ΔVj(j=1,2,…,n-1)分别为各风电场风速变化时节点j的相角和电压的变化量;ΔPh、ΔQh(h=1,2,…,l)分别为各风电场风速变化时,支路的有功功率和无功功率的变化量。 当风电场的风速变化较大时,若 则不能采用线性化潮流方程运算,需重新计算确切性潮流。进而得到风速变化后,节点电压和支路功率的变化量,即 式中,Vr、Vj分别为额定风速和实际风速下,应用确切性潮流计算得到的节点j的电压幅值;Pr、Ph分别为额定风速和实际风速下,应用确切性潮流计算得到的支路h的有功功率值。 由2.2可以计算得到各风电场出力为某一出力离散点时,系统实际的节点电压和支路功率,进而得到当各风电场出力服从表2所示的离散化联合概率分布时,节点电压与支路功率变化量的分布及其各阶矩。根据半不变量和矩之间的关系式,得到各节点电压与支路功率变化量的各阶半不变量。最后利用Gram-Charlier级数展开式可以求得各节点电压ΔX和支路潮流ΔZ的概率分布[19]。 前文为解决风电场风速波动较大,导致部分风机出力变化不满足线性化潮流方程的问题,提出了将风电场出力的概率分布离散化,逐点判断各离散点是否适用线性化潮流方程的方法,提高了随机潮流的计算精度。为进一步推广随机潮流算法在实际电力系统中的应用,结合其与DIgSILENT软件的优势,本文研究了一种数据格式转换方法,将DIgSILENT数据格式DGS转化为电力系统分析常用数据格式、即IEEE标准格式CDF(IEEE Common Data Format),提高了随机潮流程序在实际系统分析中的效率。具体实现方法见下文。 DIgSILENT软件具有灵活的用户自定义元件模型和图形化的操作管理等特点,在模型搭建方面与其他电力系统仿真软件相比更为便捷。此外,在研究新能源发电时,DIgSILENT软件可以根据需求搭建不同的元件模型,并且包含了几乎常用的所有电力系统分析的功能,如潮流、短路计算、机电暂态及电磁暂态计算和谐波分析等功能,这些优点使DIgSILENT软件在电力系统分析领域逐渐得到推广,我国很多电网的模型搭建和仿真也是应用DIgSILENT平台完成的。 然而,电力系统随机潮流及其他分析程序多采用的输入数据格式为IEEE标准数据格式CDF,而DIgSILENT软件的数据接口和数据格式DGS与CDF不同。若利用上文的电力系统随机潮流程序对实际大型电网进行分析,则需要技术人员手动将网架参数的数据格式转为CDF格式,极大的降低了计算效率,输入文件格式的限制使得随机潮流算法难以在大型实际电力系统中进行推广。 因此,本文使用软件DIgSILENT搭建仿真网络,并在此基础上进行数据接口研究,提出了一种智能接口转换方法,可以将DIgSILENT导出的DGS数据格式转换成传统电力系统程序常用的IEEE标准数据格式,使电力系统随机潮流算法更方便地应用于实际电网分析评估中[20]。此外,本文所提的接口转换模型还可以用于电力系统潮流计算、可靠性分析及风险评估等电力系统分析中,极大的提高了大型实际电力系统的分析评估效率。 DIgSILENT软件以其开放性和兼容性为用户提供与其他程序软件连接的接口,如DGS、PSS/E、NEPLAN、MATLAB 等[21]。DGS(DIgSILENT-GISSCADA)作为DIgSILENT软件的一种双向数据传输接口,可以将完整的电网模型或元件参数从外部数据源导入至软件中,或更新现有的模型。也可以从软件导出电网模型、元件参数、网络图形数据或计算结果至外部数据源,并支持选择性输出。 本文以DGS接口为基础,研究软件仿真模型数据格式的转换和兼容问题。在DIgSILENT软件中搭建好系统仿真模型后,需就导出元件参数进行设置。在DIgSILENT中有3种类型的数据分别为Element、Type和Graphic。前两类分别包含了每种元件的特性参数和标准制造数据,Graphic则记录了网架的拓扑结构和元件之间的连接关系。当每一种元件有多个输出变量时,注意变量的选择顺序是固定的,方便后面对DGS文件进行读取。在设置完元件模型及其参数变量后,即可导出DGS格式的文档。 DIgSILENT软件由于具有高度图形化的操作模式和全新的数据管理理念,逐渐在电力系统分析领域得到推广和应用,很多电网都是应用DIgSILENT软件搭建的,电网网架及电网发电机、负荷等数据是以DIgSILENT自有的方式进行存储。通过DIgSILENT的数据接口,可以导出DGS格式的电网数据格式文件,利用编写的Visual C++数据接口程序将其转换成常用分析计算的IEEE标准格式。其具体的转换步骤如图2所示。 图2 接口转换流程图Fig. 2 Flow chart of the interface transformation 1)统计以DGS数据格式表示的电力系统网架结构中每种类型电气元件的个数,包括发电机、变压器、线路和负载等。 2)读入DGS格式文件中的StaCubic模块和母线模块(ElmTerm),然后编写母线编号的过渡矩阵,过渡矩阵中各列数据分别为:矩阵每行的序号、StaCubic模块中的第一列数据、对应母线在新的标准接口文件中的编号、母线在DGS中的原始编号以及对应母线电压等级。 3)读入DGS数据格式文件中的发电机模块(ElmSym)、负载模块(ElmLod)以及并联支路模块(ElmShnt)的数据,整理出接口格式对应的各发电机和负荷的功率值,以及并联支路导纳的标幺值等。 4)根据IEEE标准格式将母线的编号、母线电压等级、母线电压幅值和相角的初值以及步骤3)计算得到的数据进行排列。 5)经过步骤4)后,读入DGS格式文件中的变压器型号模块,包括TypTr2模块以及TypTr3模块。建立变压器型号的过渡矩阵,所述变压器型号的过渡矩阵中各列数据分别为:TypTr2模块以及TypTr3模块在DGS文件中的编号、不同型号变压器各侧电压值、各类型变压器的阻抗值以及电纳值。 6)读入DGS格式文件中线路模块(ElmLne)、变压器模块ElmTr2和ElmTr3,根据公式计算IEEE标准格式中各支路电阻的标幺值、电抗的标幺值、电纳的标幺值、变比和移相。 7)经过步骤6)后,根据IEEE标准格式将支路的编号、支路首末连接的母线的编号以及步骤6)计算得到的数据进行排列。 8)设定电力系统随机潮流分析所需要的其他参数,如潮流计算的最大迭代次数、迭代收敛的精确度等等。 该接口转换程序的使用方法有两种:a)将接口程序嵌入到电力系统分析程序中,由Visual C++中的主函数进行直接调用;b)直接由接口程序程得到一个新的IEEE标准接口文档,该接口文档可以直接用于其他电力系统分析程序。此外,该接口程序导出的数据格式和传统电力系统应用软件如MATPOWER等数据格式相互兼容,提高了在DIgSILENT环境下处理大规模复杂数据的效率,使仿真不依赖于DIgSILENT运行环境,大大减少了计算时间。 式中fA(x)、fB(x)、fC(x)、fD(x)表示各客流拥塞评价指标对应于第A、B、C、D类客流拥塞风险水平的白化权函数. 本文首先以IEEE-24节点系统为算例,验证DGS数据转换接口方法的有效性和精确性。经验证该方法正确有效之后,将其应用于本文所提出的含风电电力系统随机潮流分析计算中。进而以DIgSILENT软件中搭建的新疆地区2015年规划电网实际系统为算例,验证本文所提含风电电力系统随机潮流模型的正确性以及优越性。 DIgSILENT与Visual C++数据接口转换的方法可以普遍地应用到以IEEE标准数据格式为基础的电力系统分析程序中。以IEEE-24节点系统为例验证本文所提接口转换方法的有效性。在DIgSILENT软件中搭建IEEE-24节点系统仿真模型,系统网架结构如图3所示。系统分为138 kV和230 kV两个电压等级,额定容量为100 MV·A,由24个节点,38条支路,32台发电机和5组变压器组成。 图3 IEEE-24节点系统Fig. 3 IEEE-24 bus System 由DIgSILENT软件导出IEEE-24节点系统的DGS数据格式文件后,经过数据接口转换得到用IEEE标准数据格式表示的线路参数(R、X等)。转换后的线路参数和系统实际参数对比如表2所示。 由表2可以看出,DGS接口转换程序的最大误差为0.03%,误差出现的主要原因是计算机在计算过程中截断效应,由此验证了本文所提接口转换方法的正确性,提高了随机潮流程序及其他电力系统分析程序在实际电力系统中的应用水平。 本文采用DIgSILENT软件搭建含3个相邻风电场的新疆电网,以验证本文所提考虑风电场相关的含风电电力系统随机潮流模型的正确性以及优越性。首先通过DIgSILENT接口转换程序实现DIgSILENT软件与随机潮流分析程序的对接,进而对含风电的新疆电网进行随机潮流分析。3个风电场的装机容量均为49.5 MW,由33台额定功率为1.5 MW的风机组成,各台风机的有功出力-风速模型为: 式中,k1=Pr/(vr-vci);k2=-k1vci;风机的额定功率Pr=1.5 MW;切入风速vci=4 m/s;切出风速vco=25 m/s;额定风速vr=15 m/s。 以3个风电场一年的风速数据及式(12)的有功出力-风速模型为依据,建立表1中所示的风电场出力的联合概率分布模型。风速数据以10 min为单位,一年的风速数据共52 560组。 表2 IEEE-24节点系统的参数对比Tab. 2 Comparison of parameters of IEEE-24 bus System 利用已经验证的DGS数据接口方法将系统的网架参数导出并进行格式转换。在相同电网参数的情况下,对比蒙特卡洛法和本文所提的随机潮流程序这两种方法计算所得节点电压和支路功率的越限概率,验证本算法的精度。算例中,线性化潮流的阈值ΔCf取0.005,低压越限和风险概率电压取值范围分别为V<0.97 pu和V<0.98 pu、高压越限和高压风险概率电压分别为V>1.07 pu和V>1.06 pu。 表3 节点电压越限概率对比Tab. 3 The probability of out-of-limit of node voltage 由表3可以看出,本文所提的考虑风电相关性的含风电电力系统的随机潮流模型计算结果与蒙特卡洛方法对比,误差不超过4%,精确性高。而不考虑相关性时,越限概率的最大误差达到了12.8%,误差较大,即忽略风电场的风速相关性不符合电网实际的运行情况,计算得到的越限概率较实际越限概率低,导致电网风险的低估。 为了更全面的验证所提方法的有效性和精确性,本文还采用另外两种指标从不同方面进行评估。输出变量期望值之差dEXP(取绝对值)用于评估所提方法在输出变量的准确程度[22],输出变量累积分布曲线(cumulative distribution curve,CDC)的方差和的根均方值指标[23](average root mean square,ARMS)用于分析所提方法在输出变量概率分布趋势方面的精确程度: 式中,ARMS为方差和的根均方值指标;DCi和PCi分别为蒙特卡洛方法和随机潮流程序两种方法求得点i的累积概率值。N表示在点i处选取统计点的个数。本文中N为2 000,各统计点的间距为0.000 1 pu。 节点电压幅值期望之差dEXP和ARMS如表4所示。由表中可以看出,考虑风电相关性的dEXP和ARMS都比较小,即考虑风电相关性时,随机潮流计算得到的节点电压和支路功率的分布与应用蒙特卡洛方法计算得到的分布相近;而不考虑风电相关性的指标较大,即不考虑风电相关性将会导致系统变量分布的较大偏差。 表4 节点电压幅值的ARMSTab. 4 ARMS of nodal voltage magnitude 应用蒙特卡洛方法和本文所提的考虑相关性的含风电电力系统随机潮流算法的计算时间对比,计算机操作系统为Win 7,处理器为Intel Core i3。应用蒙特卡洛方法分析系统的随机潮流状态需要7 200 s,将同样的网架结构利用DGS数据接口转换方法应用到考虑风电相关性的随机潮流分析程序后,计算时间仅需50 s,计算速度提升了100多倍。即本文所提的基于DIgSILENT的数据接口转换方法及考虑相关性的含风电电力系统的随机潮流分析模型可以在保证计算精确度的基础上,显著提高计算速度,具有很好的实用性。 传统的含风电电力系统的随机潮流方法未考虑实际风电场之间的风速相关性,同时由于数据格式的不兼容,导致其在实际电网的分析评估中难以推广应用。针对以上问题,本文提出了一种基于DIgSILENT数据接口的含风电电力系统随机潮流分析方法: 1)该方法考虑了相邻风电场之间风速相关性,建立了多风电场出力的离散化联合概率分布模型,更贴近于实际风电场出力特点。 2)引入了线性化潮流判据,逐点判断是否符合潮流方程线性化的条件,以降低风速波动较大时带来的误差,提高计算速度和精度。 3)DGS数据接口转换方法将仿真软件中电网数据格式转换成IEEE CDF。不仅解决了随机潮流模型难以在实际电网中应用的难题,还可以使DIgSILENT软件与随机潮流、可靠性分析和暂稳态评估等多种电力系统分析程序联合仿真,有助于该软件在电力系统普遍推广使用,具有较好的应用价值。 本文所提的基于DIgSILENT的数据接口转换方法及考虑相关性的含风电电力系统的随机潮流分析模型可以有效地提高实际电力系统随机潮流分析的精度和速度,具有很好的实用性。另一方面,本文提出的接口转换模型还可以应用于电力系统潮流计算、可靠性分析及风险评估等电力系统分析中,极大地提高了大型实际电力系统的分析评估效率。 [1] 刘琦. 中国新能源发展研究[J]. 电网与清洁能源,2010,26(1):1-2.LIU Qi. Studies on China’s new energy development[J].Power System and Clean Energy,2010,26(1):1-2(in Chinese). [2] 王骏. 新能源发展研究[J]. 电网与清洁能源,2011,27(12):1-7.WANG Jun. Discussions on new energy development[J].Power System and Clean Energy,2011,27(12):1-7(in Chinese). [3] 王锡凡,王秀丽. 电力系统随机潮流分析[J]. 西安交通大学学报,1988,22(2):87-97.WANG Xifan,WANG Xiuli.Probabilistic load flow analysis in power systems[J]. Journal of Xi’an Jiaotong University,1988,22(2):87-97(in Chinese). [4] BORKOWSKA B. Probabilistic load flow[J]. IEEE trans on power app-aratus and systems,1974,93(3):752-759. [5] ZHANG Pei,STEPHEN T LEE. Probabilistic load flow computation using the method of combined cumulants and gram-charlier expansion[J]. IEEE Trans on Power Systems,2004,19(1):676-682. [6] 元玉栋,董雷. 电力系统概率潮流新算法及其应用[J].现代电力,2007,24(4):5-9.YUAN Yudong,DONG Lei. New algorithm and its application to probabilistic load flow of power system[J].Modern Electric Power,2007,24(4):5-9(in Chinese). [7] DANIEL VILLANUEVA,JOSé LUIS PAZOS,ANDRéS FEIJóO. Probabilistic load flow including wind power generation[J]. IEEE Trans on Power Systems,2011,26(3):1659-1667. [8] 董雷,程卫东,杨以涵. 含风电场的电力系统概率潮流计算[J]. 电网技术,2009,33(16):87-91.DONG Lei,CHENG Weidong,YANG Yihan. Probabilistic load flow calculation for power grid containing wind farms[J]. Power System Technology,2009,33(16):87-91(in Chinese). [9] 丁明,李生虎,黄凯. 基于蒙特卡罗模拟的概率潮流计算[J]. 电网技术,2001,25(11):10-14.DING Ming,LI Shenghu,HUANG Kai. Probabilistic load flow analysis based on monte-carlo simulation[J]. Power System Technology,2001,25(11):10-14(in Chinese). [10] 别朝红,刘辉,李甘.含风电场电力系统电压波动的随机潮流计算与分析[J]. 西安交通大学学报,2008,42(12):1500-1505.BIE Zhaohong,LIU Hui,LI Gan. Voltage fluctuation of a power system with wind farms integrated by probabilistic load flow[J]. Journal of Xi’an Jiaotong University,2008,42(12):1500-1505(in Chinese). [11] FEIJóO A,VILLANUEVA D,PAZOS J L,et a1. Simulation of correlated wind speeds:a review[J]. Renewable and Sustainable Energy Reviews,2011,15(6):2826-2832. [12] 范荣奇,陈金富,段献忠,等. 风速相关性对概率潮流计算的影响分析[J]. 电力系统自动化,2011,35(4):18-22,76.FAN Rongqi,CHEN Jinfu,DUAN Xianzhong,et a1. Impact of wind speed correlation on probabilistic load flow[J].Automation of Electric Power Systems,2011,35(4):18-22,76(in Chinese). [13] 于晗,钟志勇,黄杰波,等. 采用拉丁超立方采样的电力系统概率潮流计算方法[J]. 电力系统自动化,2009,33(21):32-36.YU Han,ZHONG Zhiyong,HUANG Jiebo,et al. A probabilistic load flow calculation method with Latin hypercube sampling[J]. Automation of Electric Power Systems,2009,33(21):32-36(in Chinese). [14] 李俊芳,张步涵. 基于进化算法改进拉丁超立方抽样的概率潮流计算[J]. 中国电机工程学报,2011,31(25):90-96.LI Junfang,ZHANG Buhan. Probabilistic load flow based on improved latin hypercube sampling with evolutionary algorithm[J]. Proceedings of the CSEE,2011,31(25):90-96(in Chinese). [15] 石东源,蔡德福,陈金富,等. 计及输入变量相关性的半不变量法概率潮流计算[J]. 中国电机工程学报,2012,32(28):104-113.SHI Dongyuan,CAI Defu,CHEN Jinfu,et al.Probabilistic load flow calculation based on cumulant method considering correlation between input variables[J]. Proceeding of the CSEE,2012,32(28):104-113(in Chinese). [16] 徐玉琴,张林浩. 考虑风速相关性的风电接入能力分析[J]. 可再生能源,2014,32(2):201-206.XU Yuqin,ZHANG Linhao. Analysis on wind power penetration limit considering wind speed correlation[J].(in Chinese). [17] 朱星阳,刘文霞,张建华. 考虑大规模风电并网的电力系统随机潮流[J]. 中国电机工程学报,2013,33(7):77-85.ZHU Xingyang,LIU Wenxia,ZHANG Jianhua. Probabilistic load flow method considering large-scale wind power integration[J]. Proceedings of the CSEE,2013,33(7):77-85(in Chinese). [18] 戎晓雪,别朝红,石文辉,等.考虑风电场相关性的含风电电力系统随机潮流分析[J]. 电网技术,2014,38(8):2161-2167.RONG Xiaoxue,BIE Zhaohong,SHI Wenhui,et al. Analysis on probabilistic load flow in power gird integrated with wind farms considering correlativity among different wind farms[J]. Power System Technology,2014,38(8):2161-2167(in Chinese). [19] 王锡凡. 电力系统优化规划[M]. 北京:水利电力出版社,1990. [20] 别朝红,孙雯,戎晓雪,等. DGS数据格式与IEEE标准格式CDF的接口转化方法:中国,201410016375.7[P].2014-05-07. [21] 吕涛,韩祯祥. 电力系统仿真软件DIgSILENT介绍[J]. 华东电力,2004,32(12):37-40.L譈Tao,HAN Zhenxiang. Introduction of power system simulation software DIgSILENT[J]. East China Electic Power,2004,32(12):37-40(in Chinese). [22] YU H,CHUNG C Y,WONG K P,et a1. Probabilistic load flow evaluation with hybrid latin hypercube sampling and cholesky decomposition[J].IEEE Transactions on Power Systems,2009,24(2):661-667. [23] ZHANG P,LEE S T. Probabilistic load flow computation using the method of combined cumulants and gram-charlier expansion[J]. IEEE Transactions on Power Systems,2004,19(1):676-682.

2 含风电电力系统随机潮流模型
2.1 潮流方程线性化模型


2.2 线性化潮流方程适用性判定




2.3 状态变量概率分布求取
3 DIgSILENT数据接口技术
3.1 DIgSILENT软件导出DGS格式数据文件
3.2 DIgSILENT与Visual C++数据接口原理及实现方法

4 算例分析
4.1 DGS数据转换接口的验证

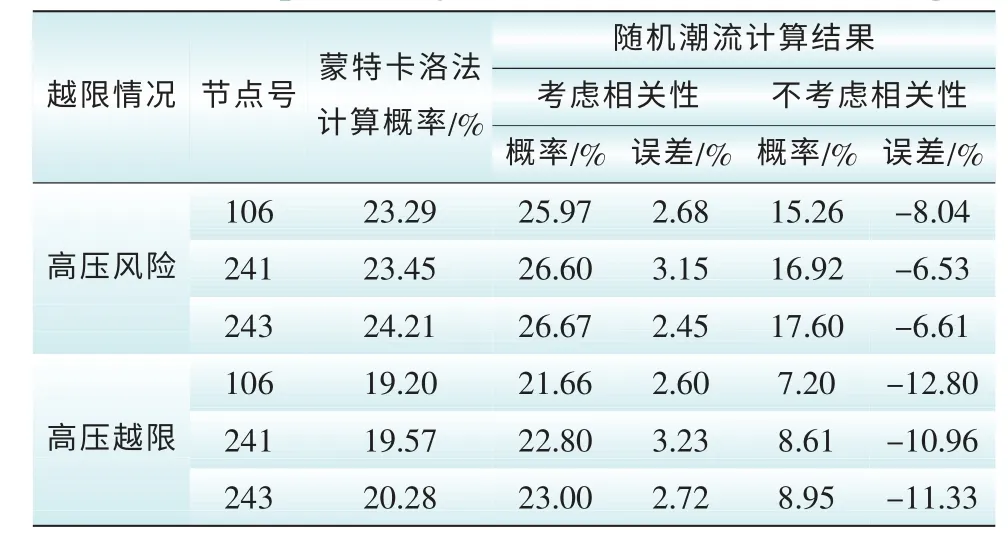
4.2 考虑风电相关性的随机潮流模型验证




5 结论

