明流泄洪洞弯道水流特性试验研究

刘小良，王鑫，姚凯，张朋鹤，杨让瑕

（1. 铜川市龙潭水库建设管理处，陕西铜川 727031；2. 西安理工大学水利水电学院，陕西 西安 710048；3. 杨凌区住房建设局，陕西 杨凌 712100）

泄洪洞作为一种泄水建筑物在水利枢纽工程中普遍存在，在实际水利工程中，泄洪洞一般为直洞，这样可以节省工程量，减小工程造价。但有些情况下，因为地质、地形、工程结构等条件的限制，泄洪洞必须设计成含有弯道的形式，以便于充分利用地形，方便工程设计施工。但随之出现的明渠高速水流，特别是泄洪洞弯道高速水流对水工建筑物影响问题也就更为突出。参考国内外工程实例可知，目前在解决该问题方面一般采用两种方法：一种是施加侧向力；一种是干扰处理。具体方法为：渠底超高法、复曲线法、斜坎法等，由于本工程已建，渠底超高法和复曲线法并不适用，因此本试验针对斜坎法做了模型试验研究，并对所出现的问题进行了研究与探讨。

1 弯道的基本情况

本文结合我国某水库导流泄洪洞弯道进行了水工模型试验。该水库导流泄洪洞布置在河道右岸，采用无压洞方案。泄洪洞为圆拱直墙型明流洞，洞身总长度492 m，断面尺寸为4.5 m×7.3 m（宽×高），底坡i=0.01，放水塔进口底板高程为680 m，弯道进口底板高程为678.929 m，洞出口采用挑流消能。水库正常蓄水位为711.591 m；设计洪水位714.76 m，下泄流量322.0 m3/s；校核洪水位719.94 m，下泄流量346.74 m3/s。弯道段详图如图1所示。

2 模型设计

根据试验任务要求，本模型按重力相似准则设计，选用几何比尺为1∶36。模型采用无色透明的有机玻璃精制而成，糙率约为0.008，通过糙率比尺换算成原型糙率约为0.014 5，接近混凝土的糙率0.014～0.015，基本满足原型泄洪洞表面的糙率要求。

图1 泄洪洞弯道段布置图及测压孔位置图Fig. 1 The arrangement of the spillway tunnel curve segment and the pressure measuring point

图2 导流泄洪洞不同开度下库水位和泄流量关系曲线Fig. 2 The relationship curve of reservoir water level and discharge with different openings of the diversion gate

3 弯道的过流条件

本次试验进行了工作闸门3.2 m全开运行工况下泄量的率定，同时还率定了弧形工作闸门局开，开度分别为0.8 m、1.6 m、2.4 m、2.8 m等4个开度下泄流量的率定工作。实测库水位为设计洪水位714.76 m时，导流泄洪洞实测下泄流量321.55 m3/s；库水位为校核洪水位719.94 m时，导流泄洪洞实测下泄流量为343.34 m3/s。根据下泄流量及弯道进口断面实测水深值，估算得出闸门3.2 m全开时弯道进口断面平均流速在19.05～22.08 m/s范围内，闸门2.8 m局开时流速在19.92～21.44 m/s范围内，弯道进口断面水流流速基本在20 m/s左右，处于高速水流研究的主要范畴。该工程明流泄洪洞的水流为高速水流，遇有弯道，将产生冲击波等问题，直接影响泄洪洞的安全运行。对于弯道下急流怎么控制，需要采取哪些措施，这是本试验所要研究的内容。

4 弯道的水流特性

4.1 弯道段的水深及流态

试验测量了原设计闸门3.2 m全开时特征库水位下弯道段的水面线；不同库水位下闸门全开时弯道外侧最高水深与弯道内侧最低水深试验结果见图3；不同库水位下闸门全开时弯道外侧最高水深与弯道内侧最低水深差值试验结果见图4；并对水流流态进行了观察，水流流态见图5，结果显示：各特征库水位下，水流在进入弯道段时，受弯道曲率半径的影响，在桩号0+108.68处凹岸水面开始升高，凸岸水面开始降低，水面产生横向坡度；在桩号0+130.28处，水面高差达到最大。实测下泄设计校核洪水时，弯道外侧最大水深超过7.3 m，水流翻越洞顶，在弯道下直洞段产生麻花水流，流态极差，有可能影响工程安全运行。同时观测得出闸门2.8 m局开时特征库水位下弯道的水面线和水流流态与闸门3.2 m全开时类似（见图6），下泄设计校核洪水时，弯道外侧最大水深在6.3～6.6 m，水流并没有翻越洞顶，但仍在弯道下直洞段产生折冲水流，相对闸门3.2 m开度流态有好转，但仍然很差。

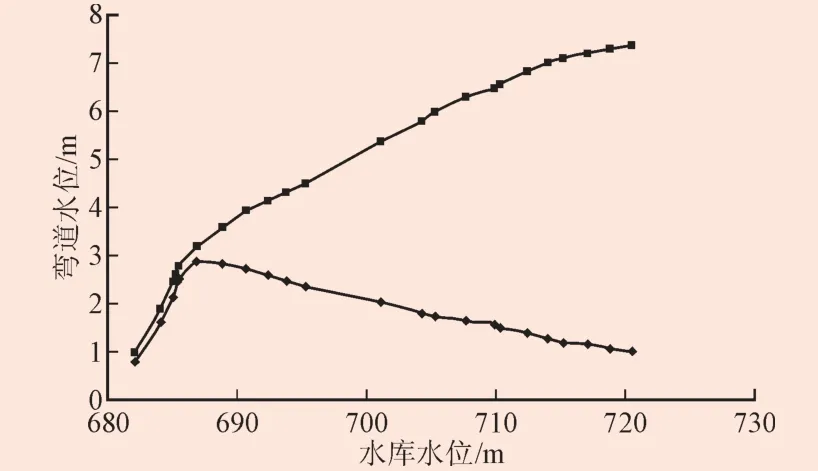
图3 闸门全开弯道外侧最高与内侧最低水深随库水位变化曲线Fig. 3 The curve of the lateral and medial depths varying with the reservoir water level when the gate is 3.2 mfull open

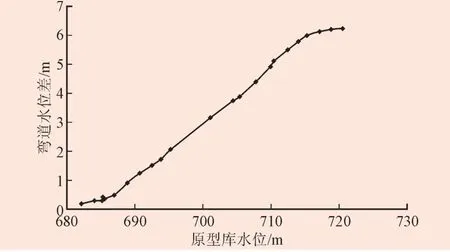
图4 闸门全开弯道外侧最高与内侧最低水深差值随库水位变化曲线Fig. 4 The curve of differences of the lateral and medial depths varying with the reservoir water level when the gate is 3.2 m full open

图5 设计洪水位下泄洪洞3.2 m全开弯道段水流流态Fig. 5 The flow regime of the curve section when gate opening full 3.2 m under the design flood level

在离心力作用下，弯道中水流表面形成从凹岸向凸岸倾斜的横向水面坡度。横向水面高差的计算采用《水力学》中的公式:

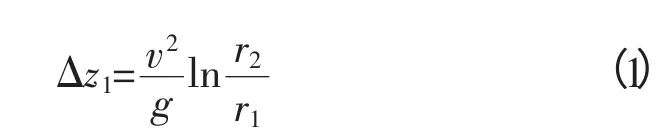
式中，r1，r2分别为弯道凸岸和凹岸的曲率半径；v为断面的平均流速。

张玉萍[1]提出：因弯段前直段水流的惯性作用顶冲凹岸时，有部分动能转化为势能而使凹岸水面升高一定数值，高速水流下，该值不可忽略。顶冲水流的横向分速vcos β的部分动能转变为势能使水位升高值为:

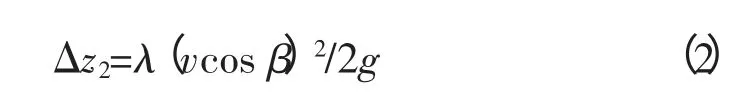
式中，β为进口直段轴线与弯段凹岸交点法线的交角，本工程为73°；λ为系数，近似取为1；v为断面的平均流速。

根据上述公式，分别估算了泄洪洞闸门3.2 m全开和2.8 m局开下各特征洪水情况下弯道的横向水面高差，闸门3.2 m全开时水面差计算值在4.72～6.33 m内，实测值在5.2～6.25 m内，闸门2.8 m局开时计算值在5.11～5.98 m内，实测值在5.0～5.87 m内。实测值与理论计算值相差不大。

4.2 弯道段的压强

由量测结果可知，随着库水位升高，弯道段压强也随之增大。各库水位下，弯道段凸岸侧壁压强沿程减小，之后随着水深逐渐升高，压强随之增大。弯道段凹岸侧壁压强沿程增大，之后随着水深逐渐降低，压强随之减小，凹岸侧壁最大压强出现于0+119.48断面附近，因弯道段前直段水流在惯性作用下顶冲于凹岸0+119.48断面附近，使得部分动能转为势能。各库水位下，弯道段底板和侧壁压强均为正值，未测到负压，尽管流态很差，但不能断定边壁一定会破坏。

由于泄洪洞已经建成，要想通过改变泄洪洞尺寸及改变弯道曲率半径来解决弯道存在的问题并不现实，因此优化只能在既定条件下进行。参考国内外已建工程的工程经验，经过分析研究，提出如下方案进行研究。

4.2.1 弯道段加设斜导流坎

斜坎[2]是一种小型导流结构，其作用是改变弯道底部部分水流的方向，使部分水流从凹岸流向凸岸，达到凹岸和凸岸水流水深平衡。本模型分别做了矩形和梯形斜导流坎的模型试验。试验方案为：从弯道进口到弯道末端加设5道斜导流坎，两坎间距7.0 m，坎高0.25 m，斜导流坎和导线夹角为45°。斜坎型式具体布置如图7所示。

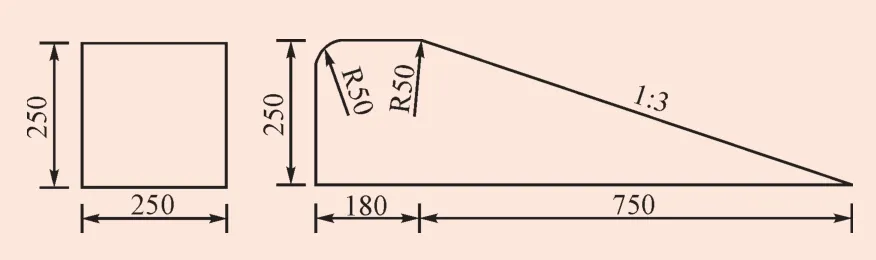
图7 矩形和梯形斜导流坎（单位：mm）Fig. 7 Rectangle oblique ridge and keystone oblique ridge（unit: mm）

实测加设斜导流坎后，水流流经弯道时，弯道内侧水深相对增高，弯道水面差大为减小。水流流态变好，下直洞段折冲水流明显减轻。对于弯道水流流态的改善，经比较，矩形斜导流坎优于梯形斜导流坎。但进一步试验发现，加设斜导流坎后，在斜坎的右边侧壁、坎后底板和导流坎顶部均有出现负压的情况，且负压值很大，实测加设矩形斜坎后，在第二道导流坎后导流洞右侧壁测点出现最小压强，其模型值为－0.57×9.8 kPa；加设梯形斜坎后，在梯形斜导流坎的顶部出现最小压强，其模型值为－0.45×9.8 kPa，由于负压值很大，容易出现空化水流问题。因此，该方案不能采用。

4.2.2 限制下泄流量

导流泄洪洞闸门下压至2.8 m开度，泄流量较闸门全开3.2 m泄量要小，下泄最大流量由346.74 m3/s减小到266.68 m3/s。由于流速在20 m/s左右，弯道段最大水面差仍很大，同一断面实测最大水面差为5.87 m，下直洞段的折冲水流仍很严重，流态仍较为紊乱，但相比较闸门3.2 m全开工况，弯道水流和折冲水流明显减弱。

5 结论

通过对泄洪洞明流高速弯道水流的研究，得出：

1）弯道水流流态及下直洞段的折冲水流流态很差；2）弯道水流使得弯道段和下直洞段过水断面尺寸偏小，在试验中对其采用工程措施进行了完善。

明流泄洪洞水流在弯道的作用下，凸岸水位降低，凹岸水位升高，严重时会引起凹岸水流翻越洞顶。因此，对高流速明流泄洪洞，工程一般不选择弯道布置。如果弯道布置难以避免，在设计弯道时应注意高速水流所引起的弯道水流问题。

由于本工程已建成，扩大断面不易实现，因此在弯道加5道矩形或梯形斜导流坎，弯道段和下直洞段流态有较大改善，但在斜导流坎的右边侧壁、导流坎后面的底板和导流坎的顶部出现负压，且负压值很大。工程最终采用限制泄洪洞下泄最大流量，限制闸门开度，水流流态得到了改善。

[1] 张玉萍. 弯道水力学研究现状分析[J]. 武汉水利电力大学学报，2000，33（5）：35-39，80.ZHANG Yuping. Simple analysis of present situation of bend channel hydraulics research[J]. Journal of Wuhan University of Hydraulic and Electrical Engineering，2000，33（5）：35-39，80（in Chinese）.

[2] 刘小江，邓军，张叶林，等. 高速明流转弯水力学问题解决方案[J]. 西南交通大学学报，2012（5）: .LIU Xiaojiang，DENG Jun，ZHANG Yelin，et al. Discussion of the solution on the hydraulic problem of turning and high-speed open flow[J]. Journal of Southwest Jiaotong University，2012（5）:（in Chinese）.