基于功率谱密度的风电功率特性分析

张旭，牛玉广，马一凡，韩永辉，张晴晴

（华北电力大学新能源电力系统国家重点实验室，北京 昌平 102206）

近几年来，我国风电装机容量迅速增长，在电网中所占比例不断提高，风电并网对电网的安全稳定运行产生了很大的影响。自然界风能的间歇性和波动性决定了风电功率具有不可预测的波动性，这正是风电对电网产生影响的根本原因。

目前针对风电功率波动特性的研究主要是集中在时域范围内的分析和研究。文献[1-3]基于实测数据建立了风电功率波动模型，并对模型精度进行了验证。文献[4]分析了风电功率波动在不同时间、空间尺度上的分布特性。文献[5]运用概率统计分析和时间序列分析方法，对风电有功功率的波动特性进行了分析。文献[6]分析了风电场的功率输出概率分布和多个风电场的联合输出功率特性。

以上文献多是从时域的角度出发，研究风电功率的波动特性，但并未完全揭示出风电功率波动随装机容量和时间尺度连续变化规律。本文基于风电场运行的实测数据，从频域的角度出发，以风电功率的功率谱密度为基础，研究风电功率波动的频域特性。

1 风电功率的功率谱密度估计

1.1 风电功率数据

本文所采用的数据为内蒙古赤峰东山风电场的实测数据。东山风电场共装机100台额定功率为2 000 kW的Vestas V80-2000型风机，总装机容量为20万kW。文中所用5 s采样周期数据起止时间为2012年9月25日至2012年10月15日，共21 d，每个采样点包含362 880个采样数据；所用1 h采样周期数据起止时间为2012年8月25日至2012年12月7日，共105 d，每个采样点包含2 520个采样数据。

图1所示为2012年9月27日单台风机和整个风场风电功率的波动情况，风电功率基准值为对应风电装机容量。从图中可以看出，随风电装机容量的增加，风电功率波动趋势一致，但相对波动幅度明显减小。

图1 单机、单个风场输出功率对比Fig. 1 Comparison of wind power between a single turbine and a single farm

1.2 功率谱密度估计方法

随机信号的功率谱密度用来描述信号的能量特征随频率的变化关系，因此对风电功率进行功率谱分析，有助于获得风电在频域的分布情况。功率谱估计可以分为经典谱估计（非参数估计）和现代谱估计（参数估计）。由于本文所采用的数据充足，所以采用经典谱估计即可获得很高的谱分辨率。

经典谱估计中最具代表性、应用最多的是周期图法及其改进方法[7]。周期图法是直接将信号的采样数据进行Fourier变换求取功率谱密度估计的方法。假定有限长随机信号序列的N点观测数据为x（n），则其傅里叶变换为

然后进行功率谱估计：

用有限长样本序列的Fourier变换计算随机序列的功率谱，估计误差不可避免。为了减少估计误差，使功率谱估计更加平滑，可采用分段平均周期图法（Bartlett法）、加窗平均周期图法（Welch法）等方法加以改进[7]。本文采用的是加窗平均周期图法（Welch法），采用MATLAB自带的pwelch函数即可实现。

Welch法谱估计是Bartlett法基础上的改进，目的是在保持Bartlett法方差性能的同时，改善其分辨率。其基本原理是对随机序列分段时，使每段数据有部分重叠，然后对每一段数据用一个合适的窗函数进行平滑处理，最后对各段谱求平均。这样可得功率谱：

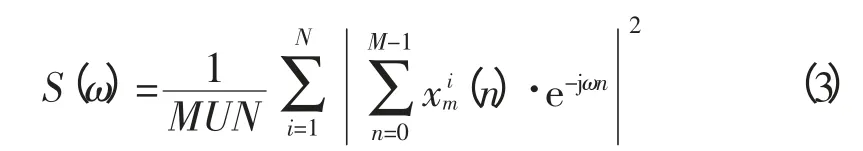
1.3 风电功率的功率谱估计实例

根据1.1节所述5 s采样周期及1 h采样周期原始功率数据，采用Welch功率谱估计方法，得到了风机功率的功率谱，功率谱图采用双对数坐标轴显示。图2所示为东山电厂10台风机5 s采样周期功率谱，图3所示为10台风机1 h采样周期功率谱，图4所示为将图2、图3功率谱结合到一起。

图2 10台风机功率5 s钟采样周期功率谱Fig. 2 Power spectrum of data sampled at 5 s resolution of the sum of ten turbines

图3 10台风机功率1 h采样周期功率谱Fig. 3 Power spectrum of data sampled at 1 h resolution of the sum of ten turbines

从图4可以看出，功率谱包含3个不同特性的区域。频率处于2×10-6与4×10-2之间，功率谱在双对数坐标图上呈现出明显的线性特性。频率大于4×10-2部分，风机的物理和电气惯性起到了低通滤波器的作用，功率谱幅值下降很快。频率低于2×10-6部分，风机最大出力上限限制了功率谱幅值的增长[8]。

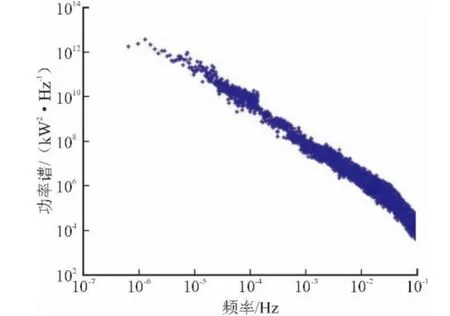
图4 10台风机功率5 s及1 h采样周期功率谱结合图Fig. 4 Combined power spectrum of data sampled at 1 h and 5 s resolution of the sum of ten turbines

将图4中线性区域部分拟合成直线，如图5所示。由于图像采用双对数坐标，因此功率谱图中线性区域部分，满足

图5 10台风机功率谱图Fig. 5 Power spectrum of ten turbines

式中，Psd为功率谱；f为频率；λ为拟合直线的斜率。此处，λ值为-1.675，即

1.4 风能谱分布理论

风能由大气湍流产生，因而对于风能的研究，其谱特性符合湍流的一般特性。大气边界层湍流运动能谱包括3个区：1）含能区（即大尺度湍流），区内浮力和切变产生湍流动能；2）惯性副区（小尺度湍流），该区内湍流动能既不产生也不耗散，而是传递给越来越小尺度的运动；3）耗散区，该区内由于流体分子粘性的作用湍流动能转变为内能。一般认为风电场所处的湍流运动能谱符合惯性副区的特点。

1941年，前苏联数学家Andrei N. Kolmogorov，提出了Kolmogorov假设[9-10]。在雷诺数足够大时，存在一个高波数区，其中湍流满足局地均匀各向同性，湍流特性仅仅决定于湍能耗散率和分子粘性系数；在局地各向同性区中还存在一个惯性副区，湍流特性只由湍能耗散率决定。根据此假设，Kolmogorov得出以下关系式：

式中，x为风速分量或温度等变量；k为波数；SS为波数谱。这就是著名的“-5/3律”。

此后，国内外许多学者对Kolmogorov的“-5/3律”进行了验证和改进[11-14]。结果均表明，在一定条件下，近地面层湍流的能谱基本上满足Kolmogorov谱分布理论，但由于不同的地理环境和气候因素，指数大小在-5/3附近有所偏差，但是能谱均在一定频域内呈指数衰减特性。

1.3节中所得10台风机的功率谱密度λ值为-1.675，在超过4个数量级的频率范围内（从2×10-6到4×10-2）符合Kolmogorov谱分布理论，时间尺度从12.5 s到2.9 d。

2 基于功率谱的风电功率波动特性分析

2.1 风电功率的汇聚效应

由于风电场覆盖地域较大，场内不同风机所接受的风能会存在空间上的差异；连接同一电网，处于不同风电场的风机接受的风能也会存在更明显的差异。风电功率波动幅度往往不随风电机组总装机容量的增长而成比例增大，我们把这种特性叫作风电功率的汇聚效应。

2.2 装机容量对风电功率波动的影响

图5给出了10台风机的功率谱，仿真结果表明，不同风机数量的功率谱图形状与图5类似，均包含3个不同特性的区域，但幅值有所变化。本文主要关注功率谱图线性区域部分随装机容量变化的特性。图6所示为100台风机功率的功率谱图，线性部分拟合直线λ值为-1.92。与10台风机功率谱图相比，λ值明显变小，但是由于装机容量的增长，同频率功率谱幅值明显增大。

图7所示为功率谱图线性区域λ值大小随风机数量变化曲线。从图中可以看出，随着风机数量的增多，λ值明显变小，即功率谱幅值随频率的升高下降速度变快。且风机数量较少时，λ值变化越明显。

图8所示为几个典型风机数量功率谱图线性部分拟合直线对比，为了方便对比，与装机容量单位保持一致，这里将功率谱幅值开平方，单位为kW/。从图中可以看出，随风机数量增长，低频部分功率谱幅值增长幅度明显大于高频部分。以10台风机和100台风机为例，装机容量增长10倍，低频2×10-6处幅值增长9.6倍，即对应于2.9 d时间尺度上的功率波动幅度增长9.6倍；高频4×10-2处幅值增长2.7倍，即对应于12.5 s时间尺度上的功率波动幅度增长2.7倍。

图6 140台风机功率谱Fig. 6 Power spectrum of 140 turbines

图7 λ值大小随风机数量变化Fig. 7 The change of λ with change of the wind turbine quantity

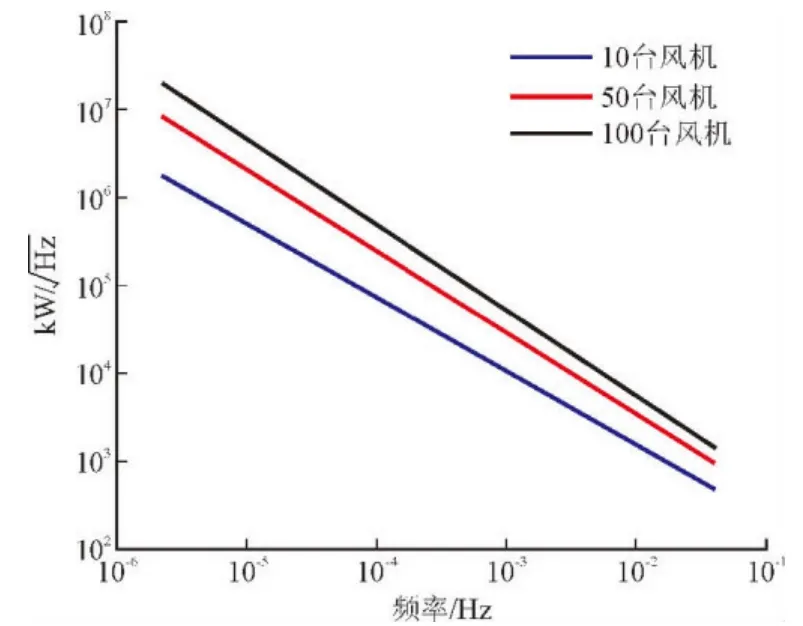
图8 典型风机数量功率谱图拟合直线对比Fig. 8 Comparison of the fitting line among different quantity of wind turbines

由以上分析可知：风电功率的功率谱幅值在线性区域随着频率的增加呈指数衰减特性，且风机数量越多，装机容量越大，衰减速度越快。随着装机容量的增加，功率谱幅值在低频处增长幅度约等于装机容量的增长幅度，但在高频处的增长幅度远小于装机容量的增长幅度。因此，频率越高，时间尺度越小，风电功率的汇聚效应越明显，从而从功率谱密度的角度论证了风电功率的汇聚效应。这说明风电装机容量的增加对于短时间内的功率波动具有明显的平抑作用。

3 结论

本文通过对风电功率实测数据进行功率谱密度估计，分析了风电功率在频域内的分布特性。结果表明，风电功率的功率谱密度分布在超过4个数量级的频域范围内符合柯尔莫哥洛夫谱分布理论，时间尺度从12.5 s到2.9 d。同时功率谱密度估计论证了风电功率的汇聚效应，且时间尺度越小，风电功率波动的汇聚效应越明显。

[1] S覬RENSEN P，CUTULULIS NA，VIGUERAS RODRíGUEZ A，et al. Modelling of power fluctuations from large offshore wind farms[J].Wind Energy，2008，11（1）:29-43.

[2] SORENSEN P，CUTULULIS NA，VIGUERAS-RODRíGUEZ A，et al. Power fluctuations from large wind farms[J].Power Systems，IEEE Transactions on，2007，22（3）: 958-965.

[3] S覬RENSEN P，HANSEN AD，ROSAS PAC. Wind models for simulation of power fluctuations from wind farms[J].Journal of Wind Engineering and Industrial Aerodynamics，2002，90（12）: 1381-1402.

[4] 崔杨，穆钢，刘玉，等.风电功率波动的时空分布特性[J].电网技术，2011，35（2）: 110-114.CUI Yang，MU Gang，LIU Yu. Spatiotemporal distribution characteristic of wind power ffluctuation[J]. Power System Technology，2011，35（2）: 110-114（in Chinese）.

[5] 侯佑华，房大中，齐军，等. 大规模风电入网的有功功率波动特性分析及发电计划仿真[J]. 电网技术，2010，34（5）: 60-66.HOU Yaohua，FANG Dazhong，QI Jun，et al. Analysis on active power fluctuation characteristics of larger-scale grid-connected win d farm and generation scheduling simulation under different capacity power injected from wind farms into power grid[J]. Power System Technology，2010，34（5）: 60-66（in Chinese）.

[6] 张义斌，王伟胜. 风电场输出功率的概率分布及其应用[J]. 电力设备，2004，5（8）: 38-40.ZHANG Yibin，WANG Weisheng. probability distribution of power output for wind power field and its application[J].Electrical Equipment，2004，5（8）: 38-40（in Chinese）.

[7] 王凤瑛，张丽丽. 功率谱估计及其MATLAB仿真[J]. 微计算机信息，2006，22（31）: 287-289.WANG Fengying，ZHANG Lili. Power spectrum sensity estimation and the simulation in matlab[J]. Micro Computer Information，2006，22（31）: 287-289（in Chinese）.

[8] APT J. The spectrum of power from wind turbines[J].Journal of Power Sources，2007，169（2）: 369-374.

[9] KOLMOGOROV AN. Dissipation of energy in locally isotropic turbulence[C]. Proceedings of the Dokl Akad Nauk SSSR，F，1941.

[10] KOLMOGOROV AN. The local structure of turbulence in incompressible viscous fluid for very large reynolds numbers[C]. Proceedings of the Dokl Akad Nauk SSSR，F，1941.

[11] RUELLE D，TAKENS F. On the nature of turbulence[J].Communications in Mathematical Physics，1971，20（3）:167-192.

[12] KAIMAL J，KRISTENSEN L. Time series tapering for short data samples[J]. Boundary-Layer Meteorology，1991，57（1-2）: 187-194.

[13] KAIMAL J.Turbulenece spectra，length scales and structure parameters in the stable surface layer[J]. Boundary-Layer Meteorology，1973，4（1-4）: 289-309.

[14] 卞建春，乔劲松，吕达仁. 大气近地层湍流能谱特征的再分析[J]. 大气科学，2002，26（4）: 474-480.BIAN Jianchun，QIAO Jinsong，L譈Daren. Reanalysis of turbulent spectra in the atmospheric surface layer[J]. Atmospheric Sciences，2002，26（4）: 474-480（in Chinese）.