UUV自航发射鱼雷过程的建模与仿真

李宗吉，任 斌，孙玉松，练永庆

(1.海军工程大学 兵器新技术应用研究所，湖北 武汉430033;2.海军装备部，北京100161)

0 引 言

水下无人航行器(UUV)，通常由水面舰或潜艇布放入水［1］。以往UUV 在用于军事领域时，通常是通过在敌方舰船下布放水雷来消灭敌舰船，但随着反蛙人及反潜技术的不断提高，UUV 在敌方控制区活动生存的概率也越来越小。如果将鱼雷作为UUV 的攻击武器，将大大提高UUV 的作用距离，其打击能力和生存能力也将得到提高［2］。

由于现有装备在潜艇上的鱼雷发射装置具有体积大、系统复杂的特点，因此UUV 发射鱼雷一般采用自航发射的方式。鱼雷从UUV 上自航发射时，鱼雷的扰动将对UUV 的航行状态产生影响。而由于UUV 自身质量轻、体积小的特点，在鱼雷发射的过程中其运动状态将会不断地发生改变，而这个改变量不可忽略，这也是UUV 发射鱼雷与潜艇发射鱼雷的区别。

1 发射鱼雷过程及模型假设

1.1 UUV 发射鱼雷过程

UUV 开始自航发射鱼雷时，鱼雷螺旋桨开始转动。在刚开始的一段时间内，鱼雷螺旋桨所产生的推力不足克服鱼雷自身所受到的阻力时，鱼雷不能沿着UUV 自航发射装置的滑轨运动。当鱼雷螺旋桨转动所产生的推力足以克服鱼雷所受到的阻力时，鱼雷便沿着自航发射装置的滑轨运动。在整个过程中，鱼雷所受到的外力将发生改变，但UUV 始终对鱼雷有一定的约束，鱼雷对UUV 也就一直存在反作用。因此UUV 的稳态将受到扰动，其运动状态发生改变，这反过来对鱼雷的运动也将产生影响。UUV 和鱼雷相互影响，直到鱼雷脱离发射导轨，发射过程完成。

1.2 模型假设

对模型作以下假设:

1)UUV 发射鱼雷前处于稳定运动状态;

2)UUV 在自航发射鱼雷过程中，UUV 推力大小不变;

3)UUV 的推力大小的调节可通过调节螺旋桨的转速来实现，且转速连续可调;

4)鱼雷在自航发射过程中，舵角始终为0。

2 UUV 发射鱼雷过程的模型

2.1 鱼雷螺旋桨的推力

鱼雷螺旋桨推力的大小与鱼雷的动力装置、螺旋桨转速、螺旋桨直径、螺旋桨叶片数量、鱼雷运动速度及海水密度等有关。鱼雷螺旋桨推力可通过以下经验公式进行计算［3］:

式中:LT为鱼雷发射深度;T0为鱼雷螺旋桨理想状态下的推力。

2.2 鱼雷对UUV 作用力的分析

鱼雷在水中受到的作用力如图1 所示。

图1 鱼雷受力示意图Fig.1 Force relationship of torpedo

鱼雷在水中运动，将受到流体的作用力(包括位置力、阻尼力、惯性力)，鱼雷在纵平面内受到的流体动力表达式如下［4］:

式中:此时设鱼雷舵角为0;MT为鱼雷质量;ρ 为海水密度;VT为鱼雷的速度;αT为鱼雷的攻角;ST为鱼雷的横截面积;ωT为鱼雷的俯仰角加速度;LT为鱼雷长度;CTx为鱼雷阻力系数;为鱼雷升力系数对攻角的倒数为鱼雷升力系数的对旋转角速度的倒数为鱼雷俯仰力矩系数对攻角的倒数;为鱼雷俯仰力矩系数的旋转倒数;λT22，λT26，λT66为鱼雷附加惯性力。

鱼雷在UUV 上自航，由于受到UUV 的约束，鱼雷将沿着滑轨做加速运动。将UUV 对鱼雷的作用力分为沿着轴向且向后的作用力XUT，垂直于轴向且向下的作用力YUT及一个力矩NUT。力XUT和YUT及力矩NUT保证鱼雷沿着自航发射装置的滑轨运动。根据鱼雷的运动模型，可知力XUT和YUT以及力矩NUT的表达式如下:

式中:PT为鱼雷的重浮力，θ 为鱼雷的俯仰角。

对于XUT的计算，则要分不同的情况:

当鱼雷推力不足以使鱼雷相对于UUV 滑动，XUT表达式如下:

式中:υ 为鱼雷与发射导轨之间的摩擦系数，TT为鱼雷的推力。

当鱼雷推力足以克服流体阻力以及滑轨的摩擦力使得鱼雷产生相对于UUV 的运动。此时XUT的表达式为:

由此也可以得到鱼雷的加速度表达式为:

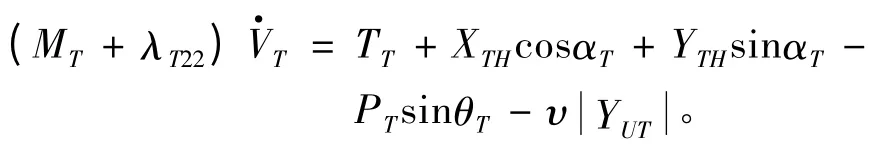
鱼雷相对于UUV 的运动方向为轴线正方向。

NUT可以理解为在除UUV 力矩之外，各力矩的综合作用下产生的旋转力矩与实际角加速度所消耗的旋转力矩之差。这部分差量等于UUV 对鱼雷施加的外力矩。NUT的表达式如下:

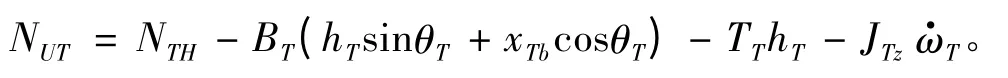
此外，XUT和YUT二力的作用点均是通过鱼雷的重心，因此二力对UUV 也会产生力矩。二力的力矩在此不作分析，在分析UUV 的综合运动模型时会将其考虑在内。

2.3 UUV 的运动模型

除流体动力之外，在UUV 上还有重力W、浮力B、推力T、以及鱼雷对UUV 的作用力和力矩。UUV 受力如图2 所示。

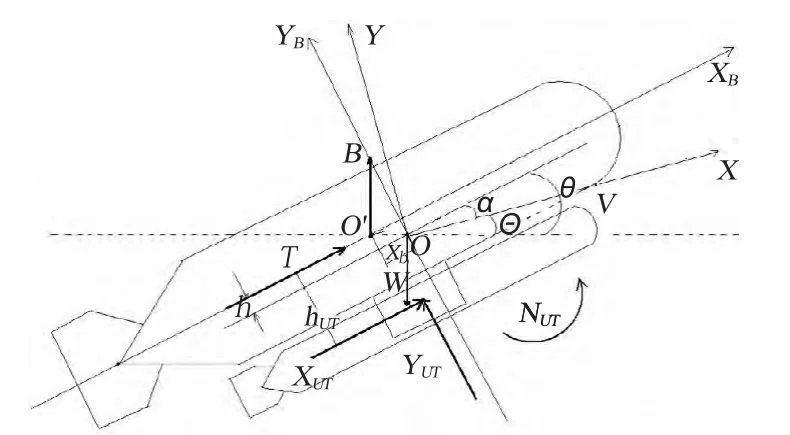
图2 UUV 受力示意图Fig.2 Force relationship of UUV

UUV 在这4 类力以及流体动力的作用下运动方程组如下:

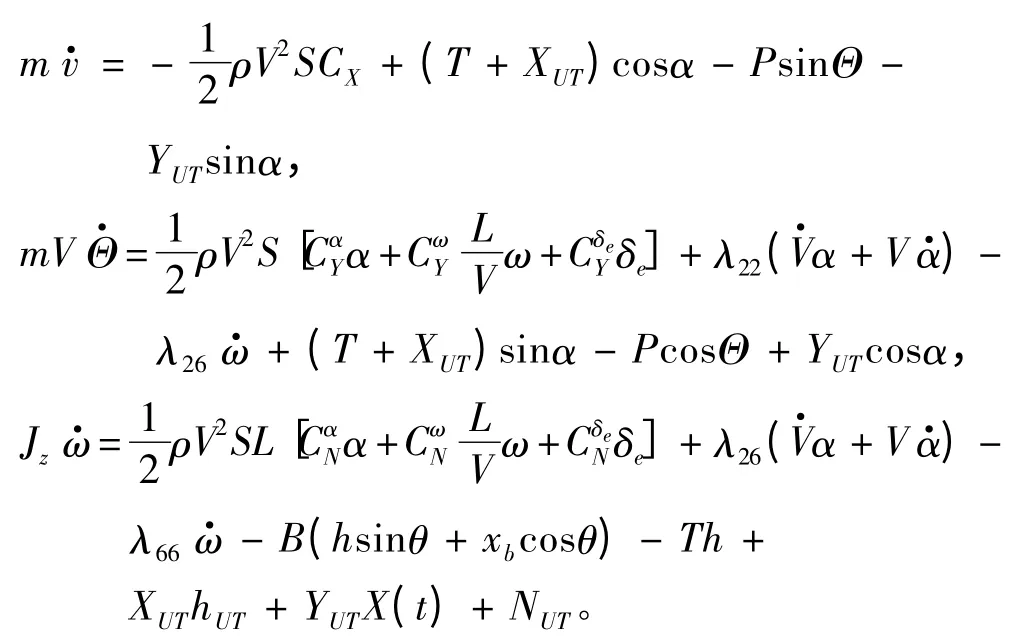
式中:hUT为鱼雷重心与重心在体坐标系OYB轴上的距离;X(t)为重心与鱼雷重心在体坐标系轴OXB上的距离;xb为浮心与重心在体坐标上的距离;T 为螺旋桨的推力;B 为浮力;O′XBYB为体坐标系;OXY 为速度坐标系;XUT为鱼雷通过与发射装置滑轨之间的摩擦对UUV 的作用力。YUT为鱼雷对UUV 在垂直于轴线方向上的力;NUT为鱼雷通过自航发射装置滑轨作用在UUV 上的力矩;V 为UUV 重心的速度。其余流体动力参数含义与鱼雷相同。

2.4 鱼雷运动参数的计算模型

鱼雷运动模型是在UUV 运动模型基础上得到的。UUV 在大地坐标系中XE方向上的速度VXE=VcosΘ，在大地坐标系中YE方向上的速度VYE=VsinΘ。设鱼雷相对于UUV 在轴线上的速度为VUT，设鱼雷的速度为VT，则可知VT= VUT+ V。

式中:VT为鱼雷相对于大地的速度;Θ 为UUV 的弹道倾角;θ 为UUV 和鱼雷总体的俯仰角;VUT为鱼雷相对于UUV 的速度;VTXE为鱼雷相对于大地在水平方向上的速度;VTYE为鱼雷相对于大地在竖直方向上的速度，根据求得的鱼雷的速度，还可以得出鱼雷的弹道角ΘT= arctan(VTYE/VTXE)，鱼雷的攻角αT= θ - ΘT。

2.5 鱼雷在发射装置中运动时间的确定

当鱼雷相对于UUV 的滑动距离大于导轨约束长度X(t)max时，鱼雷脱离UUV 的约束，完成发射。发射时间可用下式表示:

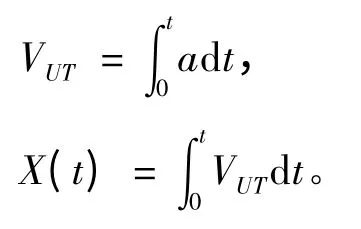
当X(tb)= X(t)max时，鱼雷脱离发射装置的滑轨，鱼雷发射完成，tb即为发射所用的时间。

3 UUV 发射鱼雷的初始条件

UUV 在发射鱼雷前应处于稳定运动状态，因此携带鱼雷的UUV 稳定运动参数即是UUV 发射鱼雷的初始运动参数。

UUV 稳定运动时，其速度、姿态角均不发生变化，且速度与水平面的夹角为0。因此UUV 的攻角与俯仰角度大小相同。UUV 的稳定运动方程组如下式所示:

式中:XUT0为XUT在初始状态时的值;YUT0为YUT在初始状态时的值;NUT0为NUT在初始状态时的值;X(0)为X(t)在t 为0 时的值。

4 变参数仿真分析

4.1 发射速度改变对发射过程的影响

在hUT= 1.5 m，PT=254 N 情况下，得到UUV分别在2 m/s，3 m/s，4 m/s 时发射某型鱼雷的初始条件如表1 所示。

表1 不同速度条件下初始运动参数Tab.1 Initial motion parameters in different velocities

从表1 可看出，随着UUV 初始速度的增大，对UUV 螺旋桨推力的要求也越大，UUV 的横舵角趋于0，UUV 的初始攻角也趋向于0。

将初始条件带入模型进行仿真，得到UUV 重心位移的曲线、UUV 俯仰角随时间的变化曲线、UUV弹道倾角随时间的变化曲线和UUV 速度随时间的变化曲线。如图3 ～图6 所示。

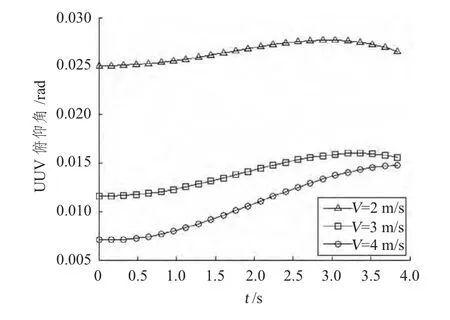
图4 UUV 俯仰角随时间的变化曲线Fig.4 Pitching angle′s over time curves of UUV

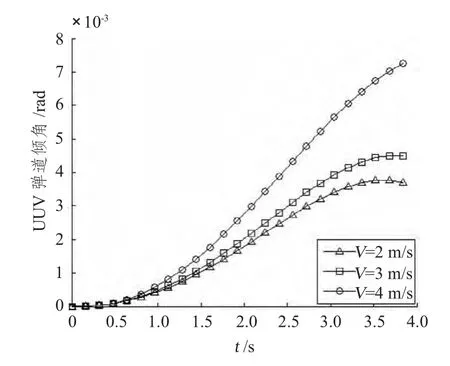
图5 UUV 弹道倾角随时间的变化曲线Fig.5 Path angle′s over time curves of UUV

图6 UUV 速度随时间的变化曲线Fig.6 Velocity′s over time curves of UUV

发射完毕时，UUV 的各参数如表2 所示。

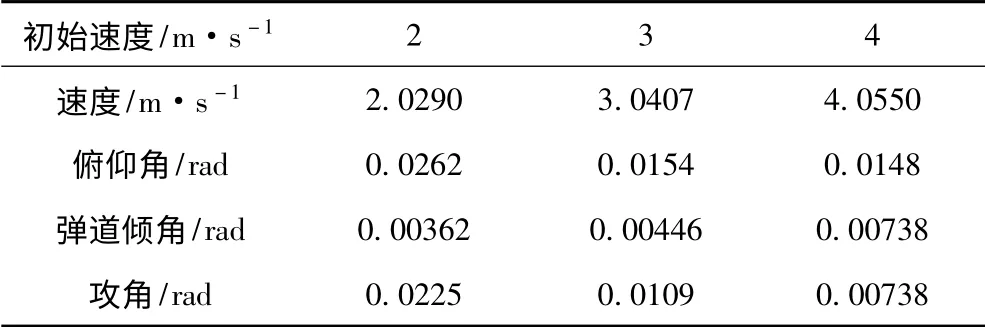
表2 发射完毕后UUV 运动参数Tab.2 Motion parameters of UUV after launching

通过改变UUV 初始速度得到的仿真结果可以看出:

1)改变UUV 初始速度对发射所用时间的影响较大，速度为3 m/s 时比速度为2 m/s 时用时少0.007 s，速度为4 m/s 时比速度为3 m/s 时用时多0.039 s。

2)UUV 初始速度越大UUV 弹道倾角变化越快，最终弹道倾角的值也越大，弹道倾角数值的数量级为10-3/rad。

3)UUV 在发射鱼雷过程中速度大小的改变量很小。

4.2 UUV 重心与鱼雷重心相对位置的变化对发射过程的影响

在V = 3 m/s，PT=254 N 时，得到hUT分别为1.2 m，1.5 m，1.8 m 时发射某型鱼雷的初始条件参数如表3 所示。

表3 不同位置条件下初始运动参数Tab.3 Initial motion parameters in different locations

由表中数据可知，随着hUT的增大，UUV 横舵角变小，UUV 初始攻角变大。

将初始条件代入模型进行仿真，得到UUV 重心位移的曲线、UUV 俯仰角随时间的变化曲线、UUV弹道倾角随时间的变化曲线和UUV 速度随时间的变化曲线，如图7 ～图10 所示。

图7 UUV 重心位移曲线Fig.7 Gravity center′s displacement curve of UUV

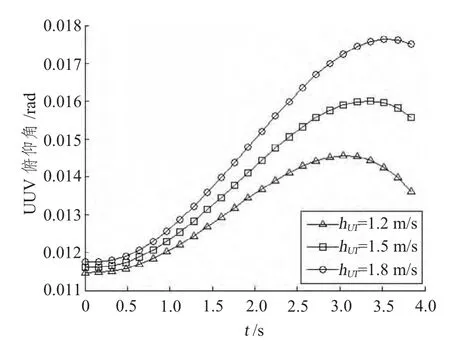
图8 UUV 俯仰角随时间的变化曲线Fig.8 Pitching angle′s over time curves of UUV

图9 UUV 弹道倾角随时间的变化曲线Fig.9 Path angle′s over time curves of UUV

图10 UUV 速度随时间的变化曲线Fig.10 Velocity′s over time curves of UUV

发射完毕时，UUV 的各参数如表4 所示。

表4 发射完毕后UUV 运动参数Tab.4 Motion parameters of UUV after launching

通过改变hUT的数值得到的仿真结果可以看出hUT越大，UUV 俯仰角越大，弹道倾角也越大，UUV 受到的扰动越大。UUV 发射鱼雷所用时间越小，但减少量较小。

4.3 挂载鱼雷负浮力的改变对发射过程的影响

在V =3 m/s，hUT=1.5 m 时，得到鱼雷重浮力PT分别为58 N，254 N，450 N 时发射某型鱼雷的初始条件参数如表5 所示。

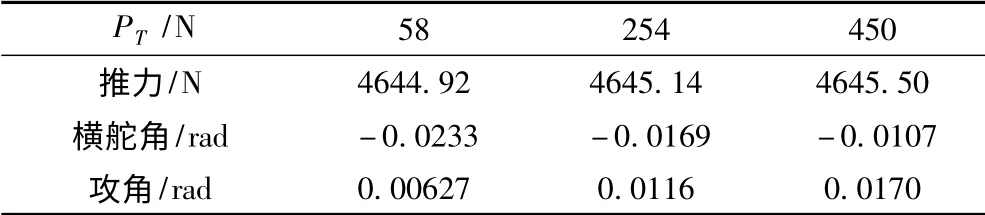
表5 不同鱼雷负浮力条件下初始运动参数Tab.5 Initial motion parameters in different negative buoyancies of torpedo

从表中可知，改变鱼雷PT越大，所需UUV 推力发生微小增加，鱼雷的舵角越大，俯仰角也越大。

将求得的初始条件代入模型进行仿真，得到UUV 重心位移曲线、UUV 俯仰角随时间变化曲线、UUV 弹道倾角随时间变化曲线和UUV 速度随时间变化曲线。如图11 ～图14 所示。

图11 UUV 重心位移曲线Fig.11 Gravity center′s displacement curve of UUV

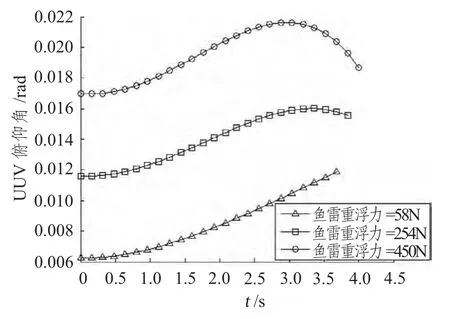
图12 UUV 俯仰角随时间的变化曲线Fig.12 Pitching angle′s over time curves of UUV

图13 UUV 弹道倾角随时间的变化曲线Fig.13 Path angle′s over time curves of UUV

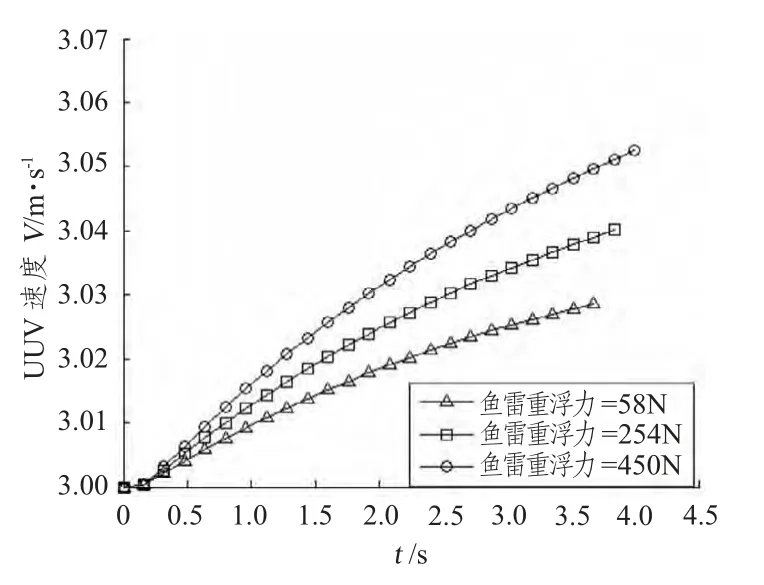
图14 UUV 速度随时间的变化曲线Fig.14 Velocity′s over time curves of UUV

发射完毕时，UUV 的各参数如表6 所示。

表6 发射完毕后UUV 运动参数Tab.6 Motion parameters of UUV after launching

通过改变PT的数值得到的仿真结果可以看出，PT越大，UUV 重心位移量越大;UUV 俯仰角度越大，弹道倾角角度开始较大，发射完毕后变小。总体来说，UUV 受到的扰动越大，UUV 发射鱼雷所用时间越长。

5 结 语

本文通过分析在UUV 自航发射鱼雷过程中鱼雷对UUV 的作用力，得出了UUV 在此过程中的运动模型。此模型得出的关于UUV 的运动数据可以为UUV 在自航发射鱼雷过程中的稳定性分析提供依据。关于UUV 自航发射鱼雷过程变参数的分析，对UUV 自航发射鱼雷试验以及自航发射装置的优化设计具有重要意义。

［1］张红.多用途无人驾驶水下航行体［J］. 水雷战与舰船防护，1997(2):21 -25.

［2］周杰，王树宗.无人水下航行器发射鱼雷初始弹道分析［J］.弹道学报，2009，21(3):86 -89.ZHOU Jie，WANG Shu-zong. Analysis of initial phase trajectory for the forpedo launched by underwater unmanned vehicle［J］.Journal of Ballistics，2009，21(3):86 -89.

［3］范凤桐. 鱼雷航行动力学［M］. 武汉:海军工程学院，1981.

［4］徐宣志.鱼雷力学［M］.北京:国防工业出版社，1992.