对概念教学的一点体会
连旸
数学概念是证明、推理和运算的依据,准确掌握数学概念是学好数学的前提和保证。学生学习数学时只重视做习题不重视对概念的理解和记忆,这样就失去了学习数学的依据,学习质量就没有保证。不从概念出发去思考问题,就不能正确理解概念,仅凭主观思想导致的错误屡见不鲜。不掌握概念而盲目去解题,只在解题方法和技巧上下功夫,这样出了错误也找不出原因。要想提高解题能力,必须理解概念,把概念掌握清楚。
初一学生刚从小学升入中学,学习上缺乏科学性,对概念理解认识不足。教师在概念数学中,要让学生准确理解概念,培养学生做到从理解、记忆、比较、叙述、应用等五方面掌握概念。
一、正确理解数学概念
每学一个新概念,首先要求学生准确理解,不能囫囵吞枣。教师在讲述概念时要讲清练透,对每个概念要逐字逐句进行分析,力求让学生真正弄懂。如讲解概念“一元一次方程”时,要向学生讲清含有一个未知数另且含有未知数的项的次数是一次的方程叫做一元一次方程。要把“元”“次”含义讲清,“元”是未知数的个数,“次”是未知数的最高指数。通过练习区别概念,在判断恒等式与方程概念实际分析外再用练习题来区别加深对概念的理解。
二、准确记忆数学概念
数学概念的记忆要做到理解记忆,不理解光会背是无用的,光理解记不准也不行。为了使学生把学过的概能记住,教师要布置作业,通过作业复习当天的概念,加深学生的理解和记忆。第二天课前提问检查,在回答问题中复习学习的概念,除回答前一堂讲的概念外还要有计划地联系比较以前讲过的概念,加强记忆,防止遗忘。依照记忆规律,学完二三天复习一次,之后一周复习一次,以后逐次延长复习时间,这样能起到复习巩固的作用。完成循环反复的记忆过程,可以使学生对学过的概念减少遗忘,用时学生会立刻想起。
三、正确叙述数学概念
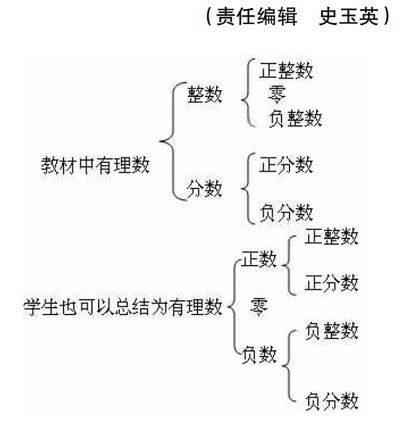
为防止学生对概念死记硬背,在概念表述上不必拘泥定义的语言和形式,让学生掌握住概念的实质,用自己的语言把所学的概念叙述出来。例如有理数的概念。 (见有理数分类插图)
四、合理比较数学概念
有比较才能有鉴别。许多数学概念相互之间联系密切,讲解新概念时,要联系已讲述过的概念,比较他们之间的异同点。如讲解“一元一次不等式”,不能只讲课本中的定义“只含有一个未知数,并且未知数的次数是一次的不等式叫一元一次不不等式。”一带而过式的讲解学生的印象不深,讲解过程要联系一元一次方程,找出的相同点和不同点。相同点都是一次一元,不同点一个是方程用符号连接,一个是不等式用不等号连接。由于有这样的异同点所以在同解原理和解法步骤上既有相同的地方又有不同的地方,通过分析异同把关键性问题突出出来,重点强调解不等式时要特别注意不等号方向是否改变的问题。对概念比较的越详细,学生就会理解得越透彻,掌握就会越准确。对于容易混淆的概念更要加以比较区别,如方程式与代数式的区别。方程含有等号是等式,代数式不含等号,分式方程和分式的区别中直接联系到恒等变形和等式运算异号,这样就会杜绝分式运算中去分母的错误做法。再如单项式与多项区别,单项式是只含有乘积的运算,而多项式是含加减运算。这些区别在讲解概念时教师必须让学生牢牢掌控,才能在做题时正确运算。
五、熟练应用数学概念
要把概念掌控牢固、严谨、精确之外,还得多练习应用,通过练习加深概念的理解记忆,用标准化试题对概念进行严格检查。标准化练习对概念理解有很多好处,可以提高学习对概念的分辨力。初中是学生打基础的时期,学生形成良好的思维习惯,才能准确快速地解答数学习题。结合概念选入一些判断题、选择题、填充题对学生加以训练可以加深学生对概念的理解,从而培养学生分析问题和解问题的能力。通过标准化练习题的训练,学生对概念的理解深刻、严谨、精确,逻辑思维能力和科学的思维方法都得到锻炼,教学效果才会明显提高。
在数学教学中,概念问题不可忽视,搞好概念教学对培养学生学习数学的能力和素质有直接的影响。
(责任编辑 史玉英)

