再析纺纱时钢丝圈在钢领上位置倾侧
周炳荣
(东华大学,上海 200051)
在文献[1]中,笔者分析得出,在不计力FMy作用时钢丝圈外脚超前角κ=0,钢丝圈平面可视为绕轴Ax'转动而前倾,以及钢丝圈前倾角χ和外倾角τ的计算。本文进一步分析计入力FMy作用时钢丝圈外脚超前角κ≠0,并指出钢丝圈的三个倾角κ,χ及τ的计算;阐明钢丝圈圈径A0M0的意义。上述内容已形成了钢丝圈—钢领几何形状设计原理,将引起钢领与钢丝圈设计、制造和使用者注意。
1 由力和力矩平衡方程式导出δ,α2,a
1.1 力矩平衡方程式
如文献[1]所述,纺纱时钢丝圈承受力FM(钢丝圈离心力)、Q(纱张力)、N(钢领支承反力)组成的平衡力系作用,三力共面且相交于一点;这三个力的作用点分别是M,J,A,且都在钢丝圈平面上,故力平面MJA即是钢丝圈平面,如图1所示。坐标系
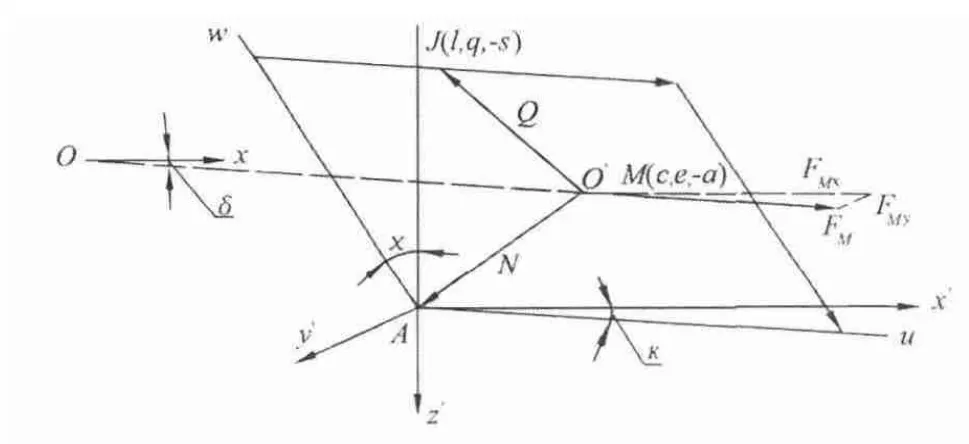
图1 钢丝圈平面MJA对于坐标平面x'Az'呈前倾
Ax'y'z'是一个平动坐标系,坐标原点设在钢丝圈—钢领接触点A。图1中,钢丝圈平面MJA的空间位置是它通过坐标原点A,在坐标平面x'Ay'上生成迹线u,以及在坐标平面y'Az'上生成迹线w。迹线w对于轴-Az'形成角χ,而迹线u对于轴Ax'形成斜角κ,表明了钢丝圈前倾和外脚超前。钢丝圈离心力FM落在其质心M绕钢领轴线z回转的径向r上,且对于轴 Ox(∥Ax')形成斜角 δ,则得分量 FMx=FMcosδ,FMy=FMsinδ。力 FM、Q 都对钢丝圈—钢领接触点A产生力矩,且互为平衡。写出每一个坐标轴上力矩平衡式,即得:
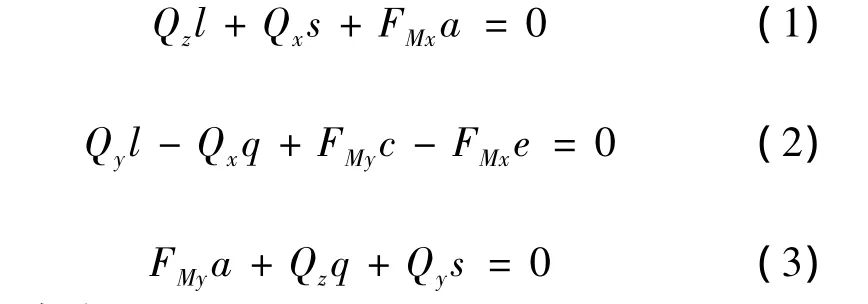
从式(1)解得
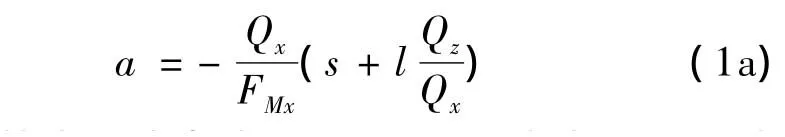
必须找出上式中诸分力的比值。根据图1绘出坐标平面x'Az'上的力三角形,如图2所示。按力平衡条件∑X'=0,得到:
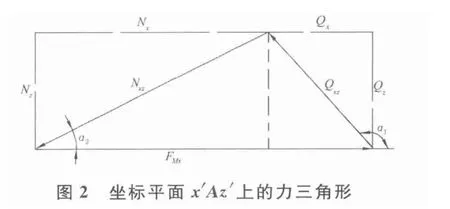
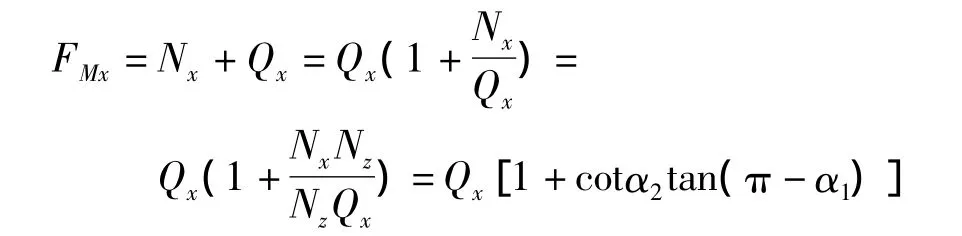
考虑到分力Qx方向为负,故下述两力的比值有负号。即:
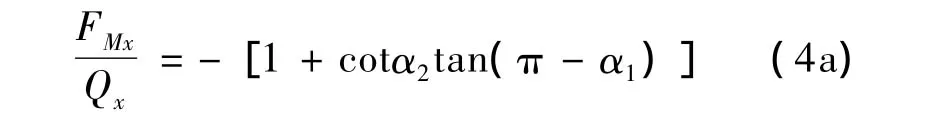
这就是说,分力以顺轴向为正,反之为负。从图2得:
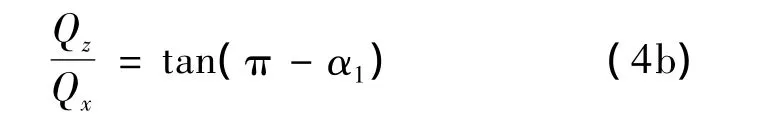
将它们代入式(1a)后得:
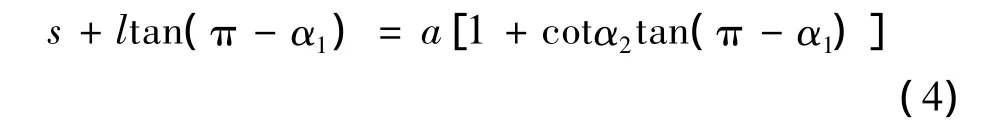
根据图1绘出坐标平面x'Ay'上的力三角形,如图3所示。因FMy=FMxtanδ,从式(2)解得:
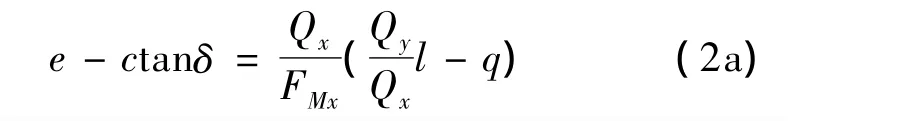
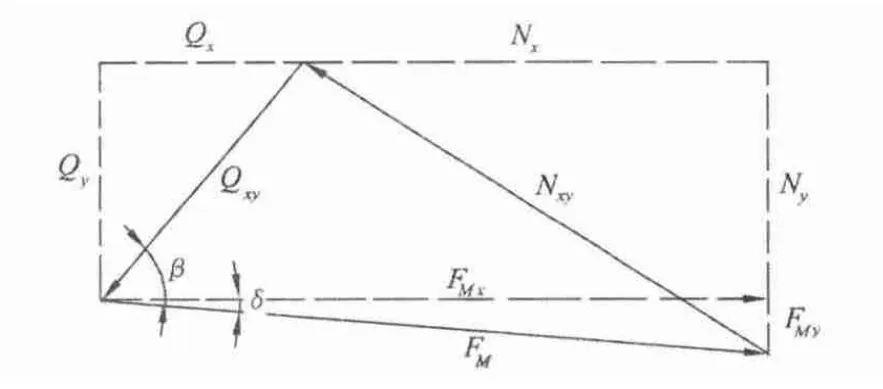
图3 坐标平面x'Ay'上的力三角形
从图3得:

又取参考文献[1]中式(18)即:
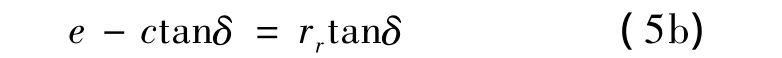
将它们代入式(2a)后得:

从式(3)解得:
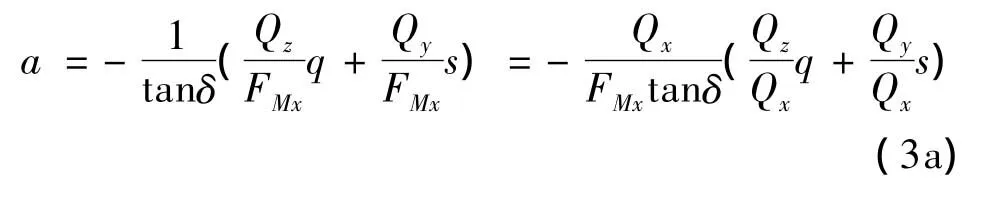
对于上式,代入式(4a),(4b),(5a),(5b)得:
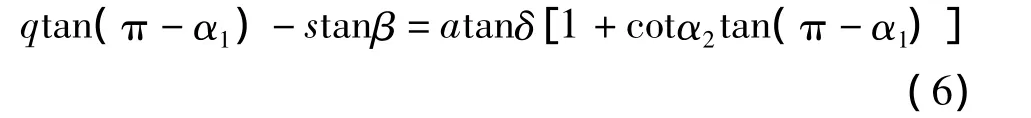
上列式(4),(5),(6)基本上从力矩平衡方程式(1)~(3)导得,其中仅使用了力平衡条件ΣX'=0。
1.2 ∠δ 与∠α2的关系式
同理,根据图1绘出坐标平面y'Az'上的力三角形,如图4所示。
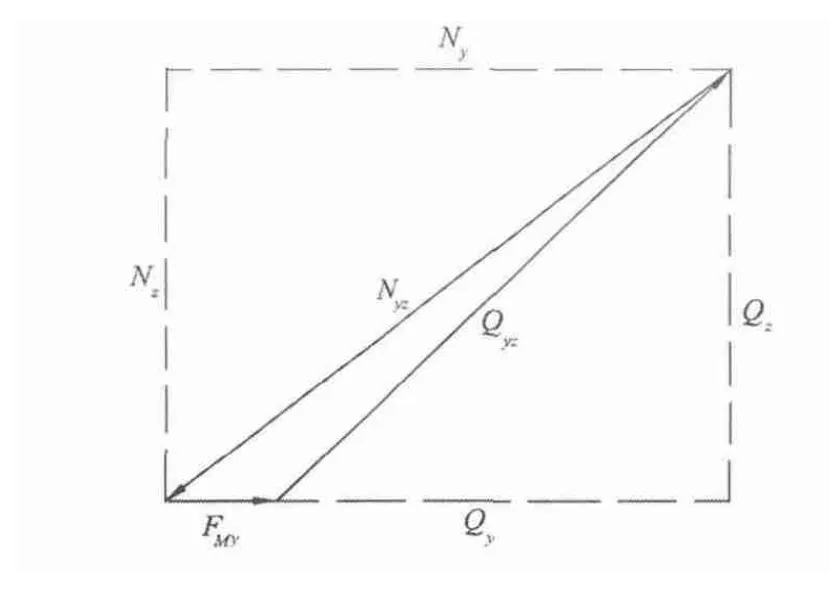
图4 坐标平面y'Az'上的力三角形
按力平衡条件ΣY'=0,可写出下式:
FMy+Qy=Ny=μNxz=F(钢丝圈受到的摩擦力)
故得:
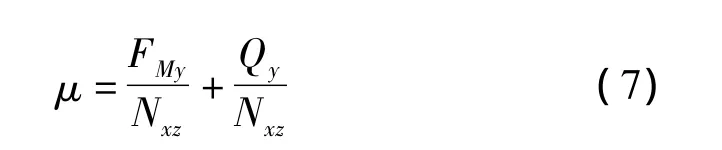
在图2中按力平衡条件ΣZ'=0,可写出下式:
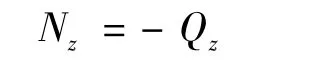
故得:
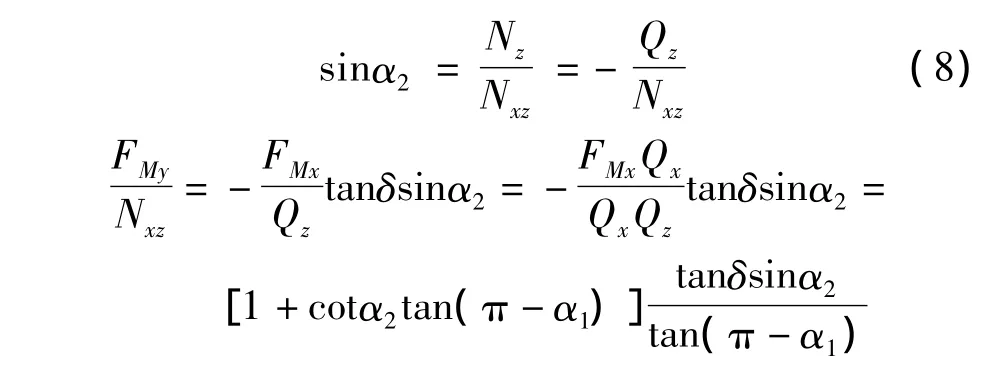
又有:
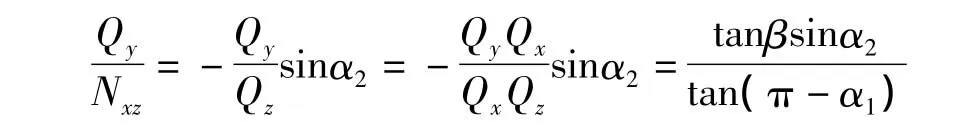
将上列两式代入式(7)得:
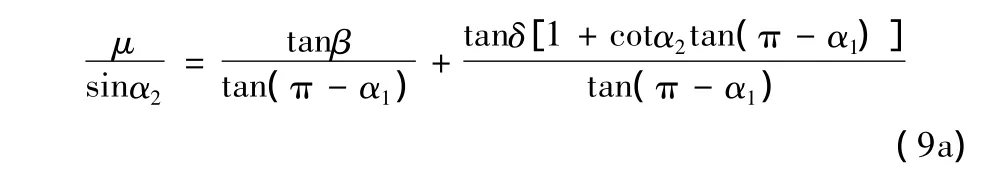
或
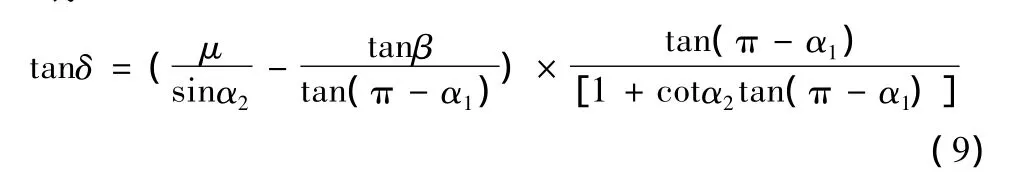
做分析计入力FMy时,钢丝圈在运动中受到的摩擦力F必定为纱张力Qy及离心力分量FMy两者之合力所平衡,如式(7)示。力FMy的计入有使力Qy减小,也就是力Q减小,导致力Nxz减小,则角α2增大(参见式(8))。可是力FMy随角δ增大而增大,因此说明角δ和α2的确有某种联系。式(9)是在参数μ,β及α1为某值时,δ-α2存在关系。该式可应用图解法中双线法求解,见图5。
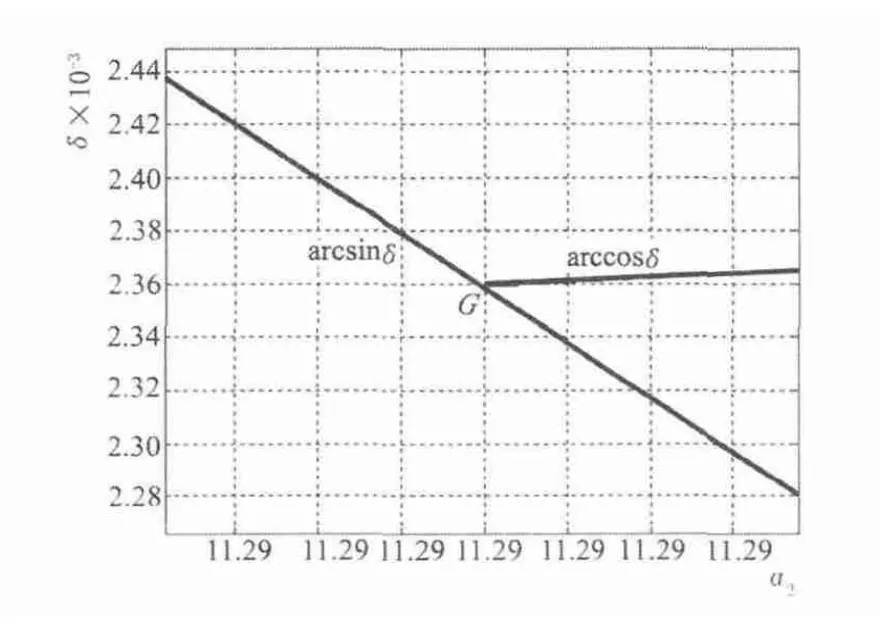
图5 曲线arccosδ及arcsinδ的交点G
某型细纱机纺T/R65/3518.5tex纱,钢丝圈6802-5/0型,钢领PG1-4554型,纱管卷装尺寸φ42 mm×180mm,卷绕短动程53.23mm。钢丝圈—钢领的摩擦因数μ=0.22;纱—钢丝圈的摩擦因数μ1=0.37。据参考文献[2]中表 6-1 可得到角 β、α1、α2及δ值,列于表1内。

表1 纺 T/R65/3518.5tex 纱时钢丝圈角 β、α1、α2、δ 计算值
从表1结果可以看出,钢丝圈位置角δ的确很小;角κ也很小,但钢丝圈外脚超前是肯定的。在正常情况下(μ=0.22),钢丝圈位置角δ的确很小;但在有金属粘连情况下,钢丝圈—钢领的摩擦因数μ则有明显的变化,角δ值及变化也就与上述结果有明显差异。
1.3 质心竖坐标a的计算
钢丝圈质心z向位置坐标a是一个重要参数,可如下解得。联立式(4)和式(6),在消去s项后得:
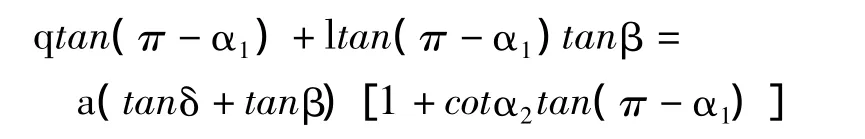
再与式(5)联立可得:
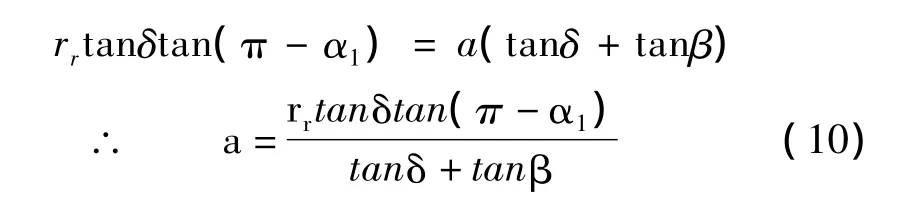
于是式(4),(5),(6)中 α1,α2,δ,a 都可视为参变数;则它是由变量l,q,s组成的线性方程组,可惜是无解的,只能采用下列方法求解钢丝圈位置倾侧角κ,χ,τ。
2 纺纱时钢丝圈在钢领上位置倾侧角
2.1 钢丝圈外脚超前角κ
在消去式(4)和式(6)的右端后得到下式:
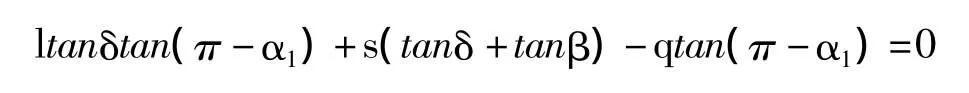
上式各项除以stan(π-α1)后得:

从式(5b)得:
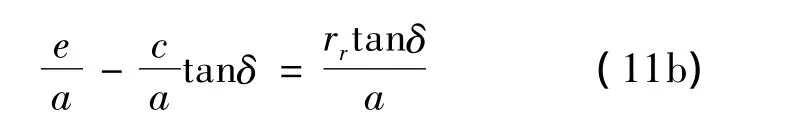
上两式在消去等式右端后得:
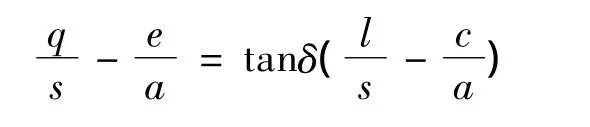
即得:
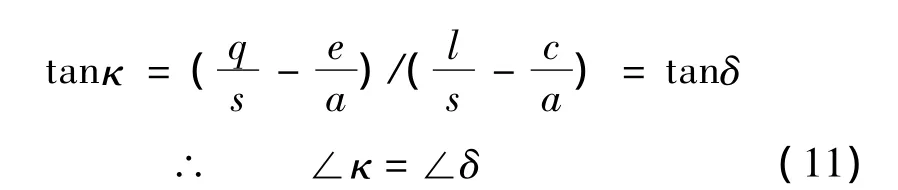
式(11)结果表明,钢丝圈外脚超前角κ等于钢丝圈位置角δ;且∠δ为正时,表示钢丝圈外脚超前于内脚,如图1所示。
2.2 钢丝圈前倾角χ
如图1所示,钢丝圈平面在坐标平面y'Az'上生成迹线w,其方程式是
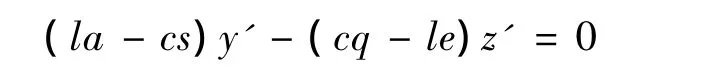
该迹线w通过坐标原点A,且对于轴-Az'的前倾角χ为:
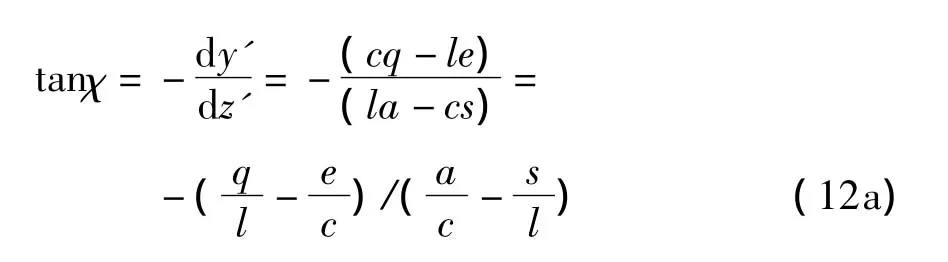
实际情况是s>l,a<c,角χ必定是正值而小于90°。由式(11a)得:
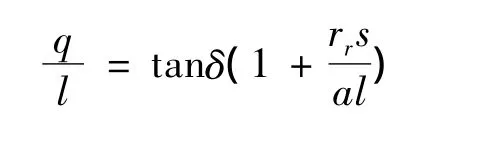
又由式(5b)得:
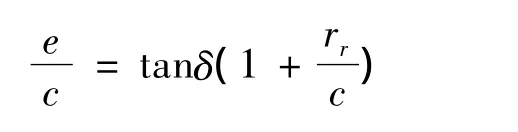
上两式相减后得:
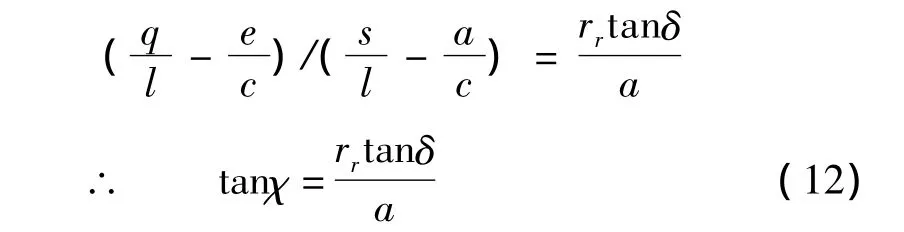
式(12)说明,钢丝圈前倾角χ随角δ及坐标a值而定。钢丝圈前倾导致钢丝圈—钢领之间纱通道减小,小到一定程度时,纱线有被轧毛或轧断之虞。对于坐标Ax'y'z'系,比值q/s表示钢丝圈上纱作用点J的前倾程度,坐标s(s=f+a)与纱通道高度hp(hp=0.5dy(1+sinα1)+ε2)成线性变化关系。
联立式(11a)与式(4)得:
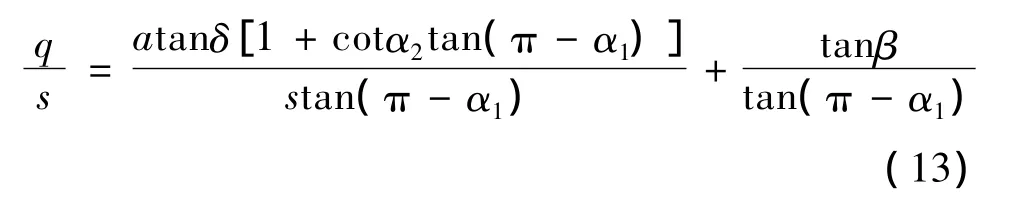
图6是钢丝圈前倾时纱线通道间隙ε2示意。在图6中,设纱截面为圆形,则得:
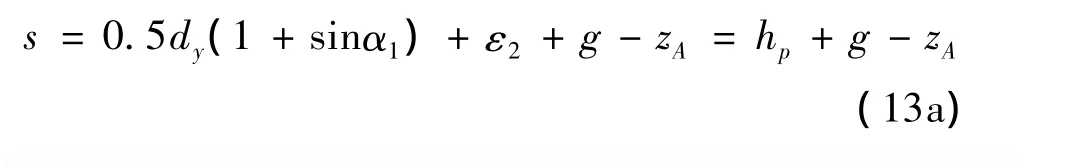
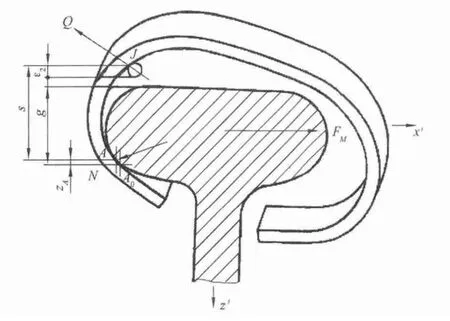
图6 钢丝圈前倾时留有纱通道间隙ε2
式中:
dy——纱直径/mm;
ε2——纱表面与钢领顶面之间间隙;
g——点A0对钢领表面的距离;
zA——点A与点A0的高度距离。
从式(13)可看出,在其他参数相同情况下,q/s与s成相反变化。即s减小,则比值q/s增大;点J的前倾增大,纱通道高度hp减小。又从图7、图8中看出:
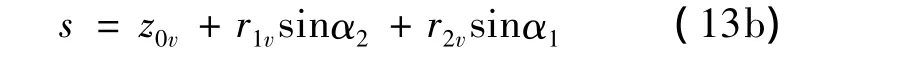
即s与钢丝圈尺寸z0和r2有关。s减小则要求尺寸z0减小和r2减小,或两者之一减小;于是钢丝圈圈形高度H及其质心M0高度减小。总之,在同样情况下,质心低、圈形小的钢丝圈前倾大,纱通道小;反之亦然。
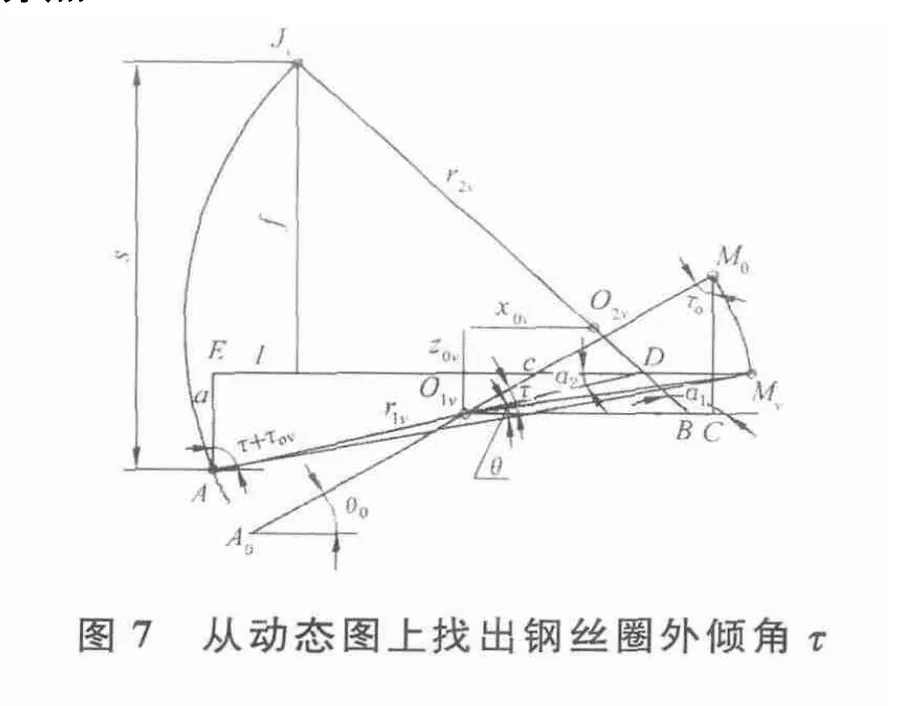

2.3 钢丝圈外倾角τ
前两节文中已讲清楚钢丝圈平面MJA的空间位置以及钢丝圈平面呈前倾和钢丝圈外脚超前。实际上钢丝圈几何图形还在此平面内呈外倾,即钢丝圈的几何形状对称线呈外倾。在坐标平面x'Az'上作动态图,找出钢丝圈外倾角τ的大小。如图7所示,点O1v是点O1在此平面上的投影点,作力三角形O1vDB。点A,Jv分别位于线O1D,BD的延长线上,点Mv落在直线ED的延长线上 。以点O1v为圆心,以O1vMv为半径画出直角三角形O1vCM0,其中∠O1vM0C=∠τ0(钢丝圈包容角),由此确定了点M0在图中的位置。已定义了钢丝圈外倾角τ值是倾斜状态的钢丝圈对于正置状态的偏转(见文献[1]中 2.1);那么图中∠M0O1vMv=∠τ,可直接量出其值。即纺纱时为适应气圈纱张力和形状需要,钢丝圈向外倾斜而其质心M0落在点Mv位置,其坐标为(c,-a);按图7可得:
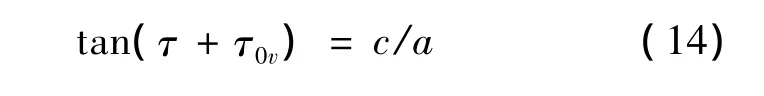
式中坐标c应由气圈纱张力和形状确定。按参考文献[1]中图9得:
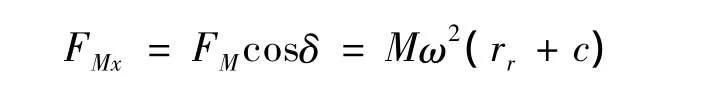
从式(4b)得:
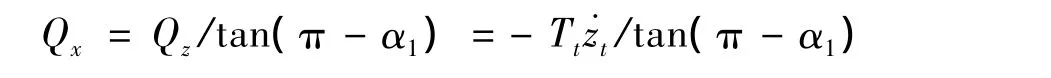
又按文献[2]中式(2-7a)得:
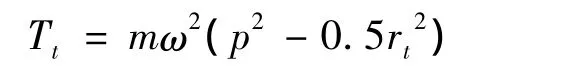
式中:
p——气圈张力参数/cm;
rt——钢丝圈上点J绕锭轴的转动半径/cm;
m——纱质量/(g·cm-1);
Tt——点 J 处纱张力/N。
于是式(4a)可演算成下式:
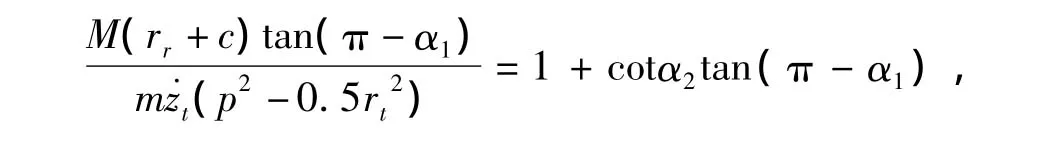
由此解得:
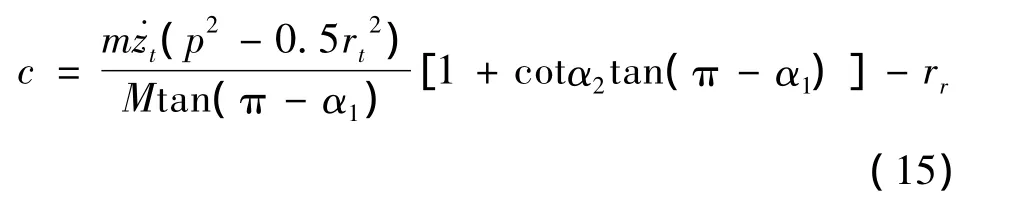
获得c和τ后,从式(14)解得:
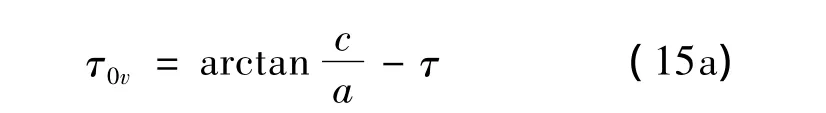
式(15a)中,τ0v是按气圈纱张力及形状和钢丝圈应具有外倾角τ要求而建立的参数。
3 关于椭圆型钢丝圈的半径A0M0*
3.1 包容角 τ0
如图8所示,点O1是钢丝圈下脚圆弧中心,点M0是钢丝圈质心。线O1M0对于钢丝圈几何形状对称线的夹角τ0称为包容角。实质上它表示了圈径A0M0(O1M0延长线)的斜度,及钢丝圈质心(点M0)对于点O1位置高度。角τ0大则钢丝圈质心位置低,圈形高度H小;反之,角τ0小则钢丝圈质心位置高,圈形高度H大。总之,角τ0能表达钢丝圈高度尺寸H。
在图7中,点D是三力平衡点,线段DMv=cacotα2,解 ΔO1vDMv可得下式:
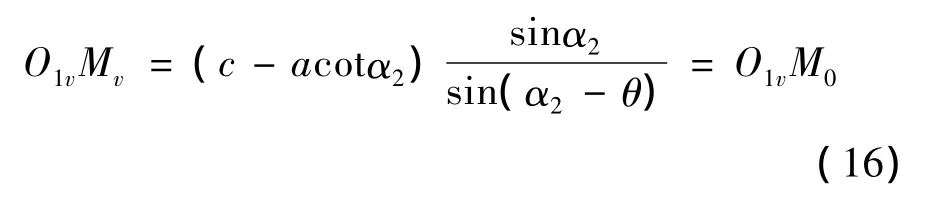
式中

又解ΔAO1vMv可得下式:
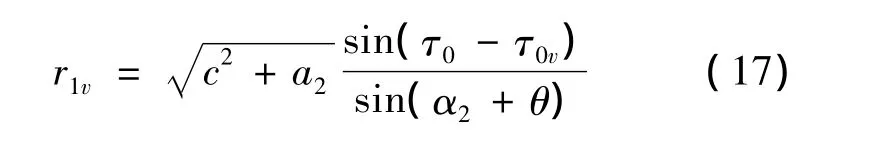
式中,α2+θ=α2-τ0-τ+90°
从式(17)可看出,r1v>0的必要条件是:

即τ0v是τ0的最小值。而τ0可从钢丝圈与钢领为弧面接触,而钢丝圈须持有工作半径r1(或r1v)解出。从图7可看出A0M0≈r1v+O1vM0,或写成下式:
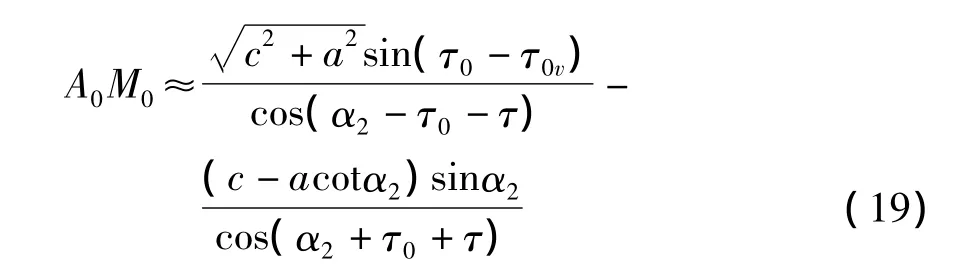
式(19)说明角 τ0和长度 A0M0相关。从式(19)还可看出钢丝圈圈径长度A0M0与参数c,a,τ,α2等值有关。每只钢丝圈都有属于自己的圈径A0M0,其长度和斜度都已确定了;可以理解在纺纱实际应用时——那时AMv≌A0M0说明它会出现不同程度的外倾和前倾。
3.2 圈径A0M0
如图8所示,将直线O1M0向该图的左下方延长一个长度r1(r1为钢丝圈下脚圆弧半径)则得点A0,线A0M0称为圈径;它的长度A0M0=O1M0+r1;斜角τ0。从图8中可以看出,长度A0M0大则钢丝圈长向尺寸D大;反之亦然。总之,钢丝圈圈径A0M0的长度和斜角指出钢丝圈圈型大小和质心位置高低,这种结果表明圈径A0M0是钢丝圈的技术特征数。
点A0是正置状态下钢丝圈与钢领的接触点,而点A是纺纱时钢丝圈与钢领的接触点,它必定在点A0的上方,那么两点位置的高度距离zA确定如下。由图7得:zA=a0-a-d。
式中,a0=A0M0cosτ0,a=ccot(τ0v+ τ),d=O1vM0
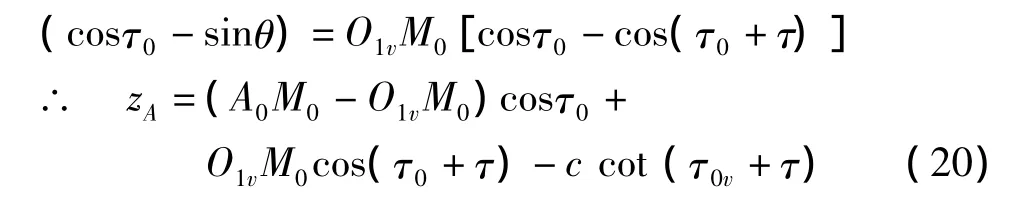
将式(13a)演化一下,则得点A0对于钢领顶面的高度距离g:
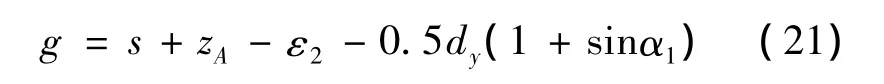
从式(21)可看出,高度g与纺纱号数,纱张力,钢丝圈圈径及通道间隙ε2等参数有关。所以,钢领跑道表面高度应足够大,容纳所使用钢丝圈要求的g。另一方面,从钢领设计方面看,钢丝圈圈径A0M0数的种类要少,点A0的空间位置变化要少。
4 结论
4.1 在计及力FMy作用时,由力矩平衡方程式
(1)~(3)导得∠κ=∠δ(见式(11)),即钢丝圈外脚超前角κ等于钢丝圈位置角δ;说明纺纱时钢丝圈外脚超前于内脚,以及外脚超前角的大小。
4.2 由式(7)及(8)导得钢丝圈位置角δ与角α2的关系式(9),采用图解法可同时解得角δ与角α2。实例计算结果表明∠δ很小,在实际分析计算时可略去。
4.3 联立力矩平衡方程式(1)~(3)可导得钢丝圈质心的竖坐标a(见式(10));但是三个线性方程式(4),(5),(6)却不能给出纱接触点 J 的坐标(l,q,-s)。
4.4 在计及力FMy作用时,钢丝圈平面MJA在坐标平面y'Az'上迹线w对于轴-Az'形成倾角χ,表明了钢丝圈前倾。对于坐标Ax'y'z'系,比值q/s表明钢丝圈上纱作用点J的前倾程度,s与钢丝圈下纱通道高度hp成线型变化。分析结果认为,在同样情况下,质心低、圈形小的钢丝圈前倾大,纱通道小;反之亦然。
4.5 纺纱时钢丝圈向外倾斜是必须的,钢丝圈外倾角τ可直接从动态图上量出(见图7);而钢丝圈质心M0坐标 c由气圈纱张力及形状确定(见式(15))。按τ和c/a算出的τ0v(见式(15a))是包容角τ0的最小值。角τ0可从钢丝圈与钢领为弧面接触,钢丝圈须持有工作半径r1的条件来选定。
4.6 圈径A0M0是椭圆型钢丝圈的技术特征数。它的斜角(∠τ0)能表达钢丝圈质心高度M0或圈形高度H;其长度A0M0能表达钢丝圈长向尺寸D。而圈径A0M0的斜度与长度有一定关联,如近似式(19)所示。
4.7 每只钢丝圈都有一个属于自己的圈径A0M0,其长度和斜度都已建立了;因为实际应用情况与原设计不一致,它在纺纱时会产生不同的外倾和前倾。圈径A0M0数的类别要少,点A0的空间位置变动要少,这样钢领跑道表面高度可以小些。
[1]周炳荣.纺纱时钢丝圈在钢领上位置倾侧分析[J].纺织器材,2013,40(3):1-8.
[2]周炳荣.纺纱气圈理论[M].上海:东华大学出版社,2010:90-112.
[3]李工博.平面对称钢丝圈的设计[J].纺织学报,1981(6):14-20.
[4]DEAE,BARRel.ThePrinciplesandTheoryofRingSpinning[M].London:TheTextileInstituteandButterworth,1965:120-127.

