基于遗传算法的悬架动力吸振器优化

潘公宇，于海浪

（江苏大学 汽车与交通工程学院，镇江 212013）

0 引言

悬架对汽车的平顺性、操纵稳定性和通过性等诸多使用性能都有很大的影响[1]。目前大多数中低档轿车使用的是被动悬架，而中高级轿车采用主动、半主动悬架居多。虽说主动悬架在车辆各种性能上优于被动悬架，但由于被动悬架具有成本低和较高可靠性等优点，所以被动悬架在中低端汽车市场仍然有广阔的发展前景。国内外已有学者对动力吸振器悬架进行了研究，但是并没有学者运用遗传算法来优化动力吸振器参数的相关研究。

汽车悬架各性能之间存在着相互制约的矛盾，研究发现，一般提高被动悬架的汽车平顺性以后，汽车车轮的高频段接地性会变差[2]，这将给汽车的行驶安全性带来较大的危害。因此，针对提高汽车平顺性会使汽车车轮高频段接地性就变差这一矛盾，本文提出在传统被动悬架基础上安装动力吸振器，并在Simulink中搭建仿真模型，通过自编译的遗传算法对动力吸振器的刚度和阻尼参数进行优化设计，改善高频段车轮接地性能。

1 建立振动模型

1.1 1/4车辆力学和数学模型

由于车轮的阻尼比较小，可以忽略不计，所以，经过简化，建立装有动力吸振器悬架的3自由度1/4车辆模型，具体结构模型如图1所示。

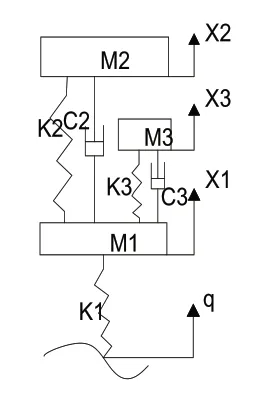
图1 装有吸振器3自由度1/4车辆模型

其中m1为非悬挂质量即车轮质量，k1为车轮刚度；m2为悬挂质量即车身质量，k2为悬架刚度，c2为减振器的阻尼系数；m3为动力吸振器质量，k3为动力吸振器的刚度，c3为动力吸振器的阻尼系数。q，x1，x2，x3,分别为路面的激励、车轮位移、车身位移和动力吸振器的位移，采用牛顿第二定律建立模型的运动微分方程，整理后得：

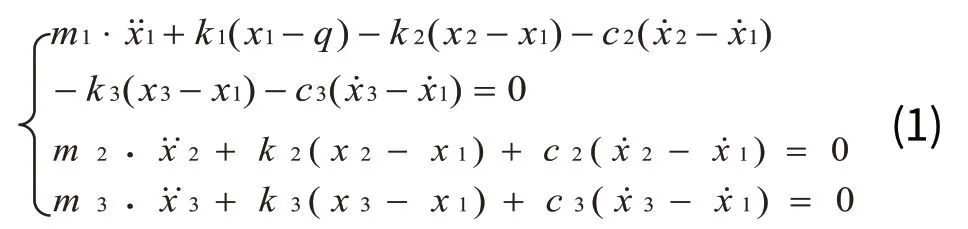
1.2 振动系统的频率响应函数和幅频特性

将式(1)的数学模型进行傅里叶变换并经过整理，分别得到x1-q，x2-x1和x3-x1的频率响应函数：

式中：j为虚数单位

系统振动响应量的幅频特性即是对该频率响应函数求模，即可得到相应的振动响应量幅频特性。

2 模型参数和评价指标的选择

2.1 悬架和吸振器参数的确定

动力吸振器共有三个参数，分别是质量m3、刚度k3和阻尼c3。根据动力吸振器和悬架在结构上关系，动力吸振器质量m3一般取车轮质量m1的0.1倍[3]。装动力吸振器的目的是为了减小高频时车轮的相对动载荷，要抵消车轮振动，理论上必须使动力吸振器固有频率f3等于车轮的偏频f1。由于，当f1=f3时就可以确定k3，本文动力吸振器刚度给出的范围是理论值上下变化20%。动力吸振器阻尼比一般取值范围在0.1～0.3之间[3]，则可确定c3的取值范围为35～130N.s/m之间。

基于某款车型选择悬架参数如表1和动力吸振器参数如表2所示。

表1 悬架参数

表2 动力吸振器参数

2.2 评价指标

汽车平顺性的评价方法主要有两种，一种是主观评价方法，另一种是客观评价方法。第一种方法因其主观性大，需要专业人员参与评价等缺点而被采用的少，第二种方法具有定量分析等优点被广泛采用。汽车平顺性客观评价的指标主要有车身加速度、悬架动行程和车轮动载荷三种[4]。本文主要是优化高频段车轮接地性能，所以，以车轮相对动载均方根值(RMS)为主要评价指标，公式[1]为：

fa、fb为积分的上下限，一般取0.89～88.51Hz[5]；为路面激励的时间功率谱密度，由国家标准制定。

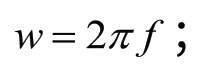
路面激励是整个模型仿真的基础，仿真模型中的路面输入模型采用的是滤波白噪声，路面输入微分方程[6]为：

式中：f0为下截止频率；G0为路面不平度系数；u为车辆行驶速度；w(t)为高斯白噪声。

选择车速为20m/s下的B级路面作为输入，根据国家相关标准，可以确定方程(2)。并且也可同时确定该路面输入Simulink模型如图2所示。

图2 路面输入模型

3 遗传算法

3.1 遗传算法的基本概念

遗传算法是基于达尔文进化论思想创建的全局优化搜索算法，最早由美国密歇根大学J.H.Holland教授在1975年提出[7]，该算法具有较强的鲁棒性和并行全局搜索能力。

遗传算法的计算过程和自然界进化类似[8]，通过对个体染色体的基因进行操作，遗传算法在计算过程中不需要了解问题的本身，它做的只是基于染色体的适应度值对个体进行评价，根据适应度值大小来选择继续繁殖的个体，最终得到最优的个体。所以，笔者编译的遗传算法不仅仅适用于本篇文章，也可用于其他模型的优化设计分析。

3.2 遗传算法运算过程

首先，算法需要随机产生n个个体，这n个个体组成算法搜索的初始种群；然后对这n个个体进行编码，分别计算n个个体的适应度值，选择适应度大的个体进行交叉和变异操作，再次计算每个个体的适应度值，存储适应度大的个体，作为下一代种群；这样经过多次进化迭代操作，最终得到适应性最高的个体。

3.3 遗传算法优化

本文编译的遗传算法是采用二进制编码方式，遗传算子是比例选择、单点交叉和基本位变异三种算子，遗传算法的参数设定：群体大小100；终止进化代数500；交叉概率0.9；变异概率0.001；离散精度取0.01。算法的适应度评价函数是轮胎相对动载均方根值的倒数，即优化变量是动力吸振器的刚度k3和阻尼c3。将上述给出的参数代入遗传算法，优化结果是c3=36N.s/m，k3=15500N/m。

4 优化结果分析

根据上述的运动微分方程和参数，在Simulink中建立装有动力吸振器的悬架仿真模型，模型如图3所示。

图3 装有动力吸振器的1/4车辆模型

对该模型进行仿真分析，在滤波白噪声路面激励下，普通被动悬架和装有动力吸振器悬架的车身加速度输出如图4所示，由图4和表3分析可得：优化前的吸振器车身加速度均方根值较普通悬架下降了3%；优化后的吸振器车身加速度均方根值较普通被动悬架下降了3.2%；优化后比优化前的车身加速度均方根值下降了0.2%。

图4 车身加速度输出对比

对悬架的性能分析一般有车身加速度、悬架动行程和车轮动载荷三种指标，本文分别给出这三种指标的均方根值，如表3所示。

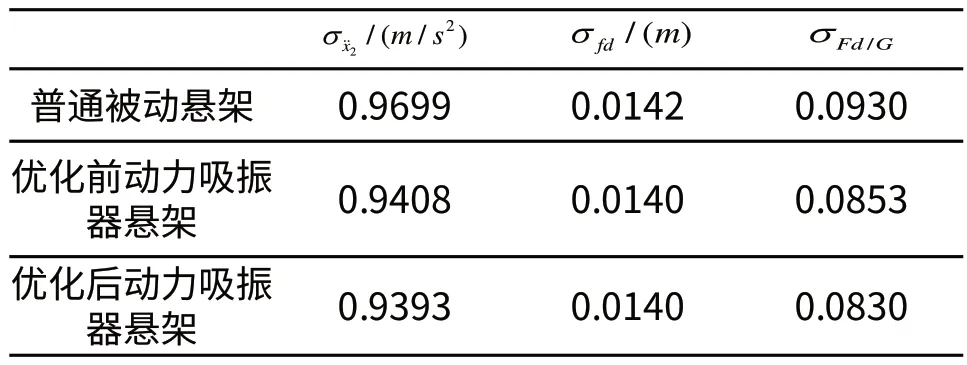
表3 均方根值对比

从表3中可以发现，其中优化前的动力吸振器悬架车轮动载荷均方根值较普通被动悬架下降了8.3%；优化后的动力吸振器悬架车轮动载荷均根值较普通被动悬架下降了10.8%；优化前后的动力吸振器悬架动行程均方根值较普通被动悬架都有下降。由此，我们可以得出，动力吸振器能够很好的改善悬架性能，并且对车轮动载荷的改善最大，因而改善车轮的接地性能，同时也可得出遗传算法对动力吸振器的优化取得了非常好的效果。

通过仿真分析得到车轮部分|x1/q|的幅频特性曲线图，如图5所示。在低频率段，三种曲线差别不是很大，接近一致，而在10Hz～15Hz之间，装有动力吸振器悬架性能优于普通被动悬架，而通过遗传算法优化后的动力吸振器性能更优。这是因为车轮的固有频率一般是在10Hz～15Hz之间[9]，本文的车轮偏频通过公式计算可得10.5Hz，动力吸振器的固有频率为11.4Hz，符合优化设计要求。

图5 |x1/q|幅频特性对比

5 结论

1）在普通被动悬架基础之上装载了动力吸振器，通过仿真研究分析，发现装有动力吸振器悬架性能优于普通被动悬架。

2）通过对幅频特性的仿真曲线分析可以发现，带有动力吸振器悬架能够更好的改善高频段车轮振动性能。应用遗传算法优化动力吸振器刚度和阻尼系数，能够进一步提高动力吸振器悬架高频段的车轮接地性能。

3）遗传算法在对结构模型的优化方面取得了非常不错的效果，可以用于其他模型的结构和特性参数优化。

[1]余志生.汽车理论(第四版)[M].机械工业出版社,2006,5.

[2]陈开景,潘公宇.带动力吸振器的空气主动悬架的仿真研究[J].机械设计与制造,2012,3(3):139-141.

[3]张孝祖,武鹏.装有动力吸振器的汽车悬架性能分析[J].江苏大学学报(自然科学版),2004,25(5):389-392.

[4]杨启耀,周孔亢,张文娜,徐兴,袁春元.半主动空气悬架Fuzzy—PID控制[J].农业机械学报,2008,39(9):24-29.

[5]赵旗,车华军,李杰.基于遗传算法的汽车行驶平顺性优化仿真[J].机械设计与制造,2009,3(3):203-205.

[6]喻凡,林逸.汽车系统动力学[M].机械工业出版社,2005,7:148-149.

[7]Hosein Habibi.Roll steer minimization of Mcphersonstrut suspension system using genetic algorithm method[J].Mechanism and Machine Theory,2008,1:58-65.

[8]M.J.Mahmoodabadi,A.AdljooySafaie,A.Bagheri.A novel combination of particle swarm optimization and genetic algorithm for pareto optimal design of a fivedegree of freedom vehicle vibration model[J].Applied Soft Computing,2013,13:2578-2585.

[9]D.Kamesh.Passive vibration isolation of reaction wheel disturbances using a low frequency flexible space platform[J].Journal of Sound and Vibration,2012,6:1310-1330.