基于Pro/E与RecurDyn的履带式管道清洗机器人的联合仿真

蔡长亮

（内蒙古工业大学 机械学院，呼和浩特 010051）

0 引言

在工农业生产及生活中，管道应用范围十分广泛。在管道的使用过程中，会产生管道堵塞与故障和损伤，需要定期进行维护、检修，但管道所在的环境往往是人们不易达到和不允许进入的，检测及清洗难度大，并且人为的清洗检修往往效率较低，因此最有效的方法之一就是利用管道清洗机器人来实现管道的在线检测与清洗，在此基础上，设计了一种履带式管道清洗机器人，用于管道的检测与维护。近年来，管道清洗机器人的研究也越来越受到人们的重视。

RecurDyn是新一代的多体动力学分析软件，采用全新的运动方程理论和完全递归算法，非常适合求解大规模复杂多体系统动力学问题。RecurDyn在行业应用子系统中提供了专业化的低机动履带包—RecurDyn/Track(LM)，文中以履带式管道清洗机器人为研究对象，利用低机动性履带包中的相应部件，通过在RecurDyn/Track(LM)环境下，仿真履带式管道清洗机器人在硬质路面上的行驶情况，获取机器人重心在竖直方向上的振动加速度、平均行驶速度、左右驱动轮转矩曲线，评价履带清洗机器人行驶时的平顺性，工作稳定性及工作可靠性。与此同时，验证了RecurDyn软件在多履带机器人运动仿真方面的突出性能表现。

1 实体建模

1.1 整机主体模型建立

清洗机器人整机主体模型主要包括机身壳体、云台、扫描仪、机械臂、连杆、工作装置（清洗刷）等刚体模型，由于RecurDyn需要采用参考点法建模，因此这些组件模型主要采用专业化三维造型软件Pro/E进行建模，所建主体模型如图1所示。

图1 主体模型

1.2 低速履带系统模型建立

履带系统主要由履带板、驱动轮、惰轮、支重轮、张紧器五部分组成，为了便于模型的建立及仿真，本文履带系统省略了支重轮模型的建立。在RecurDyn子系统环境下，利用参数化建模方法先后建立驱动轮（1个）、惰轮（1个）、张紧器（1个）三维实体模型。

利用参数化法完成各个组件模型的创建以后，应用RecurDyn软件的低速履带装配模块-SubSystem Toolkit中的 Track（LM）功能，完成整个履带系统模型的建立，该履带由34个履带板组成，每个履带可以独立设置自己的路面参数。由于左右履带系统是完全对称的，所以通过复制、粘贴、移动就可完成整个履带系统模型的建立，单个履带系统模型如图2所示。

图2 单个履带系统模型

1.3 整机装配

仿真模型是将Pro/E中建立的主体模型（不含履带系统）保存为三维软件通用格式x_ t文件，然后将其导入RecurDyn中，利用其提供的多级子系统建模和空间多接触面定义模块，完成整个管道清洗机器人机体模型的装配，整机装配如图3所示。

图3 整机装配模型

2 建立动力学模型

2.1 添加运动副

在驱动轮、张紧轮、机体等各个组件添加相应的约束，如表1所示。

2.2 定义驱动

左右两侧履带分别由2个驱动轮独立驱动，这样可以方便的实现机器人转弯动作。在驱动轮与壳体上的旋转副上施加motion驱动，利用Step（TIME，t0，y0，t1，y1）驱动函数定义驱动轮的转速，该函数的含义为时间从t0增加到t1，履带的旋转角速度由y0增加到y1。在EI中虚拟样机仿真输入具体函数值为：STEP（TIME，0，0，1，0）+STEP（TIME，1，0，3，-200D），驱动定义完成。

表1 组件间的约束副

2.3 创建路面参数

一般管道壁可以类似看成硬质路面，因此为了仿真数据的真实性，本文优先选择硬质路面作为履带爬行的媒介，设置路面与实际路面参数相似，其中内聚土壤变形模量为5.1737Pa，内摩擦土壤变形模量为0.63386Pa，土壤变形指数为0.13，土壤内聚力为6.895×10-2N，剪切阻力角度为34o，剪切变形模数为25Pa，下沉比率为5×10-2，完成路面参数设定，完整的仿真模型如图4所示。

图4 仿真模型

3 行驶系统的计算与仿真分析

1）履带机器人在硬质路面上行驶时，平均车速V为：

式中：v为实际行驶速度km/h；

nq为驱动轮转速(r/min)；

rq为驱动轮节圆半径(mm)；

σ为车辆滑转率，一般履带车辆取σ=0.05。

2）驱动转矩计算

履带机器人在硬质路面行驶时，驱动轮需要电机提供的转矩为：

式中：mg为机身总质量；

f为滚动摩擦系数，硬质路面取f=0.07。

因此，电机提供给驱动轮转矩为：

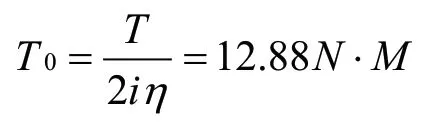
式中：i=总传动效率，取i=0.681；

3）行驶系统速度仿真分析

进行动力学仿真时，单位时间内仿真步数（step）与步长成反比，且步长越大，仿真效果越逼真明显，但仿真的计算时间相应的也越长。该驱动函数根据设计要求，将电机的转速转换成驱动轮上的角速度。仿真完成后得到的速度时间曲线如图5所示。

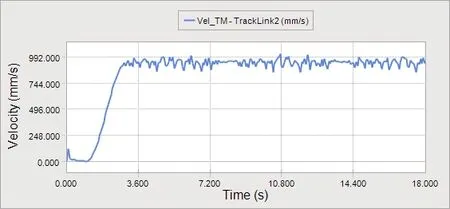
图5 硬质路面行驶速度曲线

本次仿真设置的仿真时间为18s，仿真步长为250。由仿真速度曲线可以得出：清洗机器人在0～2.8s阶段属于履带加速阶段，履带从静止状态加速到971mm/s，加速度可近似看成匀速加速度。此后，从2.8～18s这一阶段，清洗机器人以987mm/s恒定速度运行。清洗机器人稳定时运行的速度约为3.55km/h，与理论计算值3.42km/h比较，误差为3.9%，满足设计要求。由图可以看出，清洗机器人在稳定运行阶段（清洗阶段），速度在一定范围内上下波动，但波动范围较小，并且呈现一定周期性，周期约为5.7s，进一步证明清洗机器人在硬质路面上运行较平稳、稳定，工作可靠。

4）驱动轮驱动转矩仿真分析

左、右履带是分别单独驱动的，左、右履带系统驱动轮上的驱动转矩如图6、图7所示。

分析左右驱动轮驱动转矩图可以得出：清洗机器人在硬质路面上行驶时的最大驱动转矩产生于右侧履带，为495.4N·M，发生在电机启动后4.7s，此时从仿真动画中可以看出，履带开始加速，驱动转矩瞬时增大。稳定运行后，右侧履带平均驱动转矩为121.6N·M，左侧履带平均驱动转矩为120.7N·M，在理论计算值范围之内。

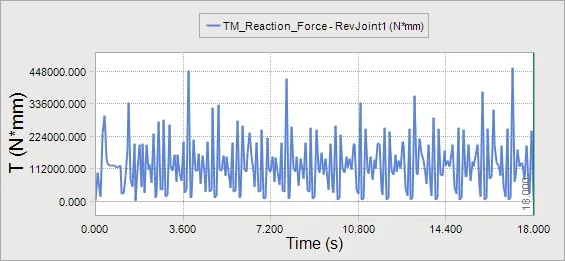
图6 左侧履带系统驱动轮驱动转矩

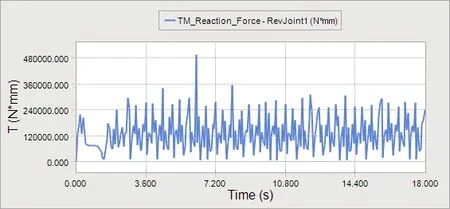
图7 右侧履带系统驱动轮驱动转矩

5）整机重心在竖直方向上的振动加速度仿真分析

履带系统在水平硬质路面从静止启动到加速到3.42km/h开始稳定运行。为了更好的分析管道清洗机器人在工作时行驶的平顺性，利用RecurDyn仿真得到了整机重心在竖直方向上的振动加速度与时间曲线，如图8所示。

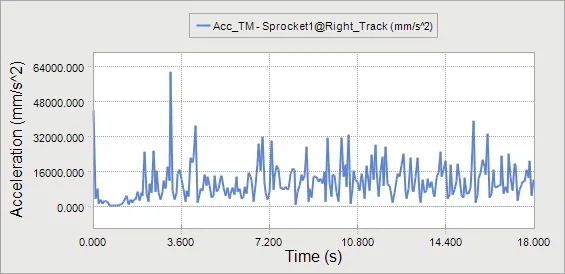
图8 整机重心在竖直方向上的振动加速度

由整机重心的振动加速度曲线可以得出：清洗机器人从启动运行到稳定行驶，机体重心振动加速度变化的范围是2.56m/s2～34.48m/s2在整个过程中，振动加速度的均值为16.52m/s2，由图可知，在刚开始启动时，加速度波动范围比较大，这是由于电机启动时瞬时扭矩较大造成的。

4 结论

本文运用三维绘图软件Pro/E与多体动力学仿真软件Recurdyn，共同建立了履带式管道清洗机器人的仿真模型。对行驶系统的速度与转矩进行了计算，并且对其在硬质路面上行驶过程进行了仿真分析，获得了机器人在硬质路面上行驶的速度、驱动轮的驱动转矩、履带机器人整机重心在竖直方向上的振动加速度曲线。仿真结果一方面体现了Recurdyn在柔性仿真方面的优点，另一方面验证了履带式管道清洗机器人在工作时行驶较平稳、可靠，但在工作过程中，履带振动加速度较大，这说明机体结构及机器人的实时控制有待进一步改进。此结论为今后管道清洗机器人的结构优化设计以及更精确的控制具有重要的指导意义。

[1]袁浩.UG机械设计实例教程.[M].北京：化学工业出版社,2007.

[2]韩宝坤,张宇,李晓雷.履带模型与仿真.[J].计算机仿真,2003(5)：7-9.

[3]郝建滨,马振书,孙华刚.基于UG和RecurDyn的排爆机器人的精确建模及动态分析[J].起重运输机械,2011(9)：62-64.

[4]吴大林,马吉胜,王兴贵.履带车辆地面力学仿真研究.[J].计算机仿真,2004(12)：42-44.

[5]焦晓娟,张湝渭,彭斌彬.RecurDyn多体系统优化仿真技术.[M].北京：清华大学出版社,2010.