加速度谐波失真度对速度型地震计振动台标定的影响

马洁美 滕云田 左爱斌 范晓勇 张 炼

1）中国北京100081中国地震局地球物理研究所

2）中国北京100013中国计量科学研究院

引言

振动台测试作为地震计的直接标定方法，在获取地震计的传递特性方面具有非常重要的实际意义（中国地震局监测预报司，2003）.然而振动台在实际运行时存在着各种非线性因素，使得振动台输出的激励信号并不是一个纯正弦运动，而是含有各类谐波（魏燕定，2001）.GB／T13823.11—1995（中国计量科学研究院，1995）中规定0.1Hz以上频率，振动台的加速度波形失真度应小于3%；International Organization for Standardization of Switzerland（1999）中要求，1Hz—10kHz频率范围内功率放大器和振动台的加速度谐波失真度（以下简称失真度）不超过2%.但在0.1Hz以下频段，国际及国家标准均未规定用何种波形，也未规定合格的界限，以至于造成一定程度的混乱（杨巧玉，舒毓龙，2011）.同一个振动量的波形失真度有加速度、速度和位移3种表述形式，而位移失真度与加速度失真度可相差10倍左右（杨巧玉，舒毓龙，2011）.本文针对地震计振动台测试存在的失真度问题，通过理论推导，设计出实时监控振动台面加速度波形、速度波形、地震计输出的速度波形及其对应失真度的振动信号数字化测量系统，并通过相关试验验证了加速度波形及其失真度对提高地震计振动测试准确程度的有效性.

1 谐波失真度的理论计算与推导

一个失真的周期振荡信号电压，除含有基波电压分量外，还含有各次谐波分量，把周期失真的正弦信号展开成傅里叶级数（马月辉等，2001），可表示为

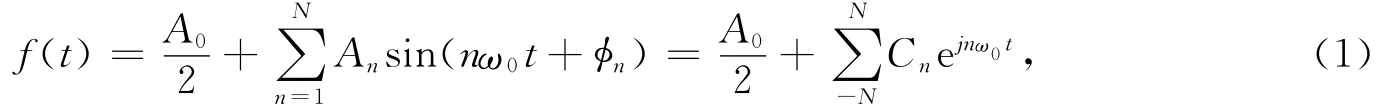
式中：f（t）为一个含有谐波失真的正弦波；An为第n次谐波的振幅，N为失真正弦波中所含最高谐波次数，An＝2｜Cn｜＝2｜C－n｜，Cn＝（1／T）∫T0e－jnω0tdt，n＝1，2，…，N；A0／2为正弦波中的直流分量；ω0为标准正弦波的角频率；φn为第N 次谐波相对于基波的初相角.

一般情况下，类正弦波信号的失真度，可用所有谐波能量之和与基波能量之比的平方根表示.如果负载与信号频率无关，则信号的失真度也可以定义为全部谐波电压的有效值与基波电压的有效值之比，即

式中：u1为基波电压的有效值；u2，u3，…，un为各次谐波电压的有效值.即n＝1，2，…，N.

若以ux表示波形f（t）的总有效值，则按照有效值定义有

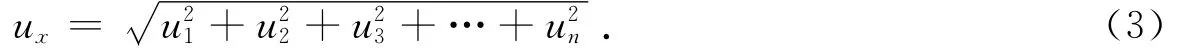
根据式（2）、（3）可导出由于波形失真所产生的信号相对变化量为

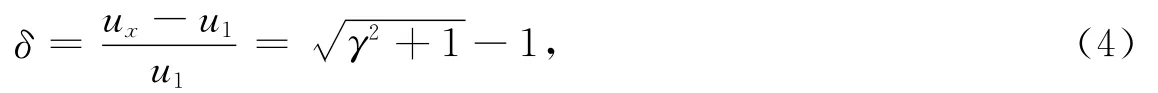
根据泰勒级数展开，γ≪1，忽略高次项，取前两项有

将式（5）代入（4），得到实际测量值ux与纯正弦波形测量值u1之间的相对偏差δ为

若振动台的输出信号以下式表示加速度量：

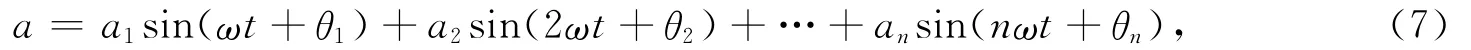
则振动速度可表示为

式中，θnn＝θn＋π／2.

根据式（2），加速度波形失真度可表示为

速度失真度表示为

显然，γv＜γa.

根据式（6），则有在同样失真度量值情况下，加速度波形失真度对测量值的影响大于速度波形失真度.

2 基于Labview的低频振动信号与失真度测量

基于美国国家仪器公司研发的实验室虚拟仪器工程平台（laboratory virtual instrument engineering workbench，简写为Labview），本文设计出低频振动信号数字化测量系统（图1）.该测量系统硬件开发平台采用美国国家仪器有限公司的数据接口卡PCI-1200及与其兼容的计算机，基于Labview虚拟仪器技术实现了对低频振动信号及其失真度的数字化测量.

图1 基于Labview的振动信号数字化测量系统示意图Fig.1 Sketch of measurement system for digitalized vibration signal based on Labview

该测量系统中，采用Labview丰富的信号处理、测量和分析函数功能，以最小二乘法为核心的正弦逼近法解调同步采集的两路正交激光干涉信号，得到振动台正弦振动的幅值，并结合同步采集的地震计输出信号进行分析处理，最终得到振动台振动加速度、速度和位移信号以及地震计灵敏度幅值和相移.失真度测量程序主要由4部分组成：硬件初始化模块、采集参数设置模块、读出模块和数据处理计算模块.采用基-2快速傅里叶算法分别得到信号基波和各次谐波系数，计算其失真度.

图2给出了振动台测试频率为1Hz（速度为4.99mm／s）时的台面输出加速度波形，其失真度为0.3%.

以中国测震台网仪器质量检测中心（以下简称质检中心）垂直振动台为例，对中国计量科学研究院研发的石英挠性加速度计SA704与适配器MSA-I组成的振动套组进行测试，并以该套组作为低频振动基准装置量值传递的标准器和核查标准，对该质检中心垂直振动台与在0.1Hz—50kHz频率范围内对直线振动传感器幅值和相位测量能力达到国际先进水平（于梅，2007）的中国计量科学研究院标准振动台进行了比对测试，测试结果见表1.

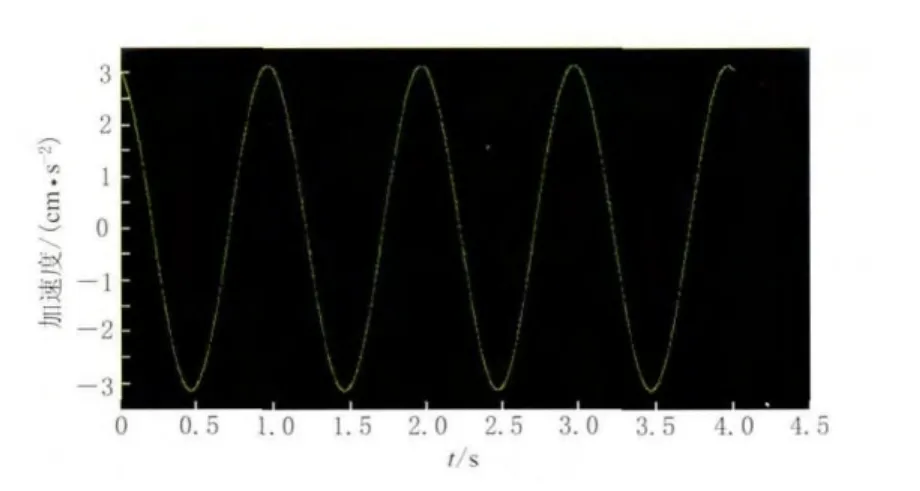
图2 频率为1Hz时的台面输出加速度波形Fig.2 Acceleration waveform of the shake table at 1Hz

表1 标准套组在中国测震台网仪器质量检测中心垂直振动台上的测试结果及其与计量院标准振动台的比对结果Table 1 Measurement results of the standard set on the vertical shake table of China Seismograph Network Equipment Testing Center and comparisons with standard values of National Institute of Metrology

表1中所测频点的加速度波形及其失真度均小于1%；质检中心振动台对振动套组的测试结果与计量院标准振动台给出的灵敏度数值偏差较小.比对结果表明，质检中心振动台及失真度测量系统可为地震计的振动检测提供测试平台.

3 地震计振动台测试中失真度表述形式对测试结果的影响

利用Labview的低频振动信号及其失真度测量系统，对英国宽频带地震计生产厂家Guralp公司的CMG-3ESPC宽频带地震计进行了测试，测试频点为1Hz.在该频点，Guralp公司给出的灵敏度出厂值为983V／m／s.表2给出了不同振动速度下台面加速度波形失真度、速度波形失真度及地震计输出的速度波形失真度、灵敏度（取3次测试平均值）的测试结果.可以看出，随着台面运动速度的增大，台面输出的加速度、速度及地震计输出的速度失真度均呈下降趋势.在该频点，通过多次地震计振动测试表明，当输入速度在地震计所能承受最大速度的50%—90%之间选取时，台面输出的加速度波形及其失真度均小于1%.当振动速度为0.182 8—1.138 1mm／s时，其加速度波形失真度较大，最大可达7.02%；而速度失真度没有出现较大波动，除了在0.182 8mm／s和0.228 9mm／s时其失真度超过1%，其余均在1%以内.然而在该速度范围内所对应的灵敏度数据则与出厂值存在一定的偏差.其原因可能是当振动速度较小时，由于功放输出信噪比很小，使得振动台的台基扰动和空气导轨气噪声对台面的干扰愈发明显，导致台面输出波形的信噪比减小，出现加速度波形严重失真，如图3所示.

表2 测试频点为1Hz时随速度变化的台面和地震计输出数据Table 2 Output of the shake table and seismometer with the velocity at 1Hz

图3 台面输出的加速度波形与速度波形比对Fig.3 Comparisons between output acceleration and velocity of the shake table

随着测试频率向更低方向的不断扩展，振动台信噪比变差.当测试频率一定时，提高信噪比的有效途径就是增大振动台的行程（魏燕定，2000）.表3给出了测试频点为0.05Hz时，逐渐增加振动台的行程所得到的台面输出加速度波形和速度波形的失真度数据.图4给出了加速度波形和速度波形失真度随行程的衰减关系.从表3和图4可以看出，随着行程的不断增大，加速度波形和速度波形的失真度不断减小，前者的减小幅度更为明显.图5a，b分别给出了行程由4mm增至23.9mm时加速度波形和速度波形的变化.同样可以看出，加速度波形变化较速度波形变化明显，且更能直观地反映出行程不断增大带来波形质量的明显改善.

图4 加速度波形和速度波形失真度随行程的衰减关系Fig.4 Distortion attenuation of acceleration waveform （circle）and velocity waveform（square）with the displacement

表3 测试频点为0.05Hz时随行程变化的台面输出波形失真度数据Table 3 Waveform distortion data of the shake table with the displacement at 0.05Hz

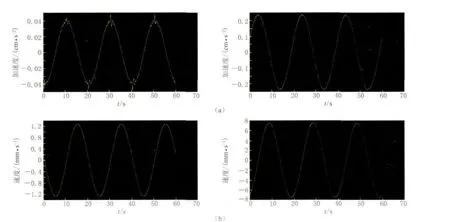
图5 行程由4mm（左）增大至23.97mm（右）时的加速度波形变化（a）与速度波形变化（b）Fig.5 Changes of acceleration waveform （a）and velocity waveform （b）with the displacement increasing from 4mm （left）to 23.97mm （right）

4 讨论与结论

从理论推导和实验验证可以看出，对于同组振动波形，其加速度波形失真度与速度波形失真度相比，前者值较大，而且对振动波形的精度描述更为严格.例如1Hz时，利用振动台对地震计进行灵敏度测试，若只是监控振动台输出的速度波形，则很容易出现这样一种情形，即速度波形失真度很小，而加速度波形失真度则已经超出IS016063.11—1999中对标准振动台加速度波形失真度2%的要求（International Organization for Standardization，1999），从严格意义上讲，此时得到的地震计灵敏度数据是不可用的.

目前我国振动基准频率的下限仅为0.1Hz，而大动态、宽频带地震计的广泛应用，迫切需要基于振动台开展低频、甚低频的测试技术研究.振动台产生理想的正弦振动激励信号是实现宽频带地震计精确校准至关重要的先决条件，而台面波形失真度则是振动台主要计量性能指标中最为主要的指标（于梅等，2011）.本文提出以加速度波形失真度指标作为约束，更有利于界定地震计振动台测试数据的合理使用范围，可为基于超低频地震计测试技术的进一步研究提供依据，对规范地震计的振动台测试工作具有积极意义.

马月辉，石彦从，王颜芳.2001.基于FFT的低频谐波失真度测试仪［J］.自动化与仪器仪表，（6）：30-32.

Ma Y H，Shi Y C，Wang Y F.2001.The design of instrument of distortion measuring［J］.Automation and Instrumentation，（6）：30-32（in Chinese）.

魏燕定.2000.超低频标准振动台波形失真度近似解析解［J］.振动与冲击，19（3）：49-51.

Wei Y D.2000.Approximate analytical solution of waveform distortion of ultra-low frequency standard vibrator［J］.Journal of Vibration and Shock，19（3）：49-51（in Chinese）.

魏燕定.2001.激光干涉仪测量失真正弦波形位移误差估计式［J］.仪器仪表学报，22（2）：199-202.

Wei Y D.2001.Error evaluation formula of measuring harmonic distortional sine wave’s amplitude with laser interferometer［J］.Chinese Journal of Scientific Instrument，22（2）：199-202（in Chinese）.

杨巧玉，舒毓龙.2011.低频标准振动台失真度及测量［J］.世界地震工程，27（2）：185-189.

Yang Q Y，Shu Y L.2011.Distortion of low frequency standard vibration table and measurement methods［J］.World Earthquake Engineering，27（2）：185-189（in Chinese）.

于梅.2007.低频超低频振动计量技术的研究与展望［J］.振动与冲击，26（11）：83-86.

Yu M.2007.Research prospects of metrology technology for low-frequency and super low-frequency vibration［J］.Journal of Vibration and Shock，26（11）：83-86（in Chinese）.

于梅，刘爱东，何闻，杨丽峰，胡红波，左爱斌，马明德.2011.石英挠性加速度计在超低频振动国家基准研制中的应用研究［J］.计量学报，32（3）：253-257.

Yu M，Liu A D，Hen W，Yang L F，Hu H B，Zuo A B，Ma M D.2011.Application of the quartz-flexure accelerometer to the development of ultra-low frequency vibration national primary standard device［J］.Acta Metrologica Sinica，32（3）：253-257（in Chinese）.

中国地震局监测预报司.2003.数字地震观测技术［M］.北京：地震出版社：51-53.

Department of Earthquake Monitoring and Prediction，China Earthquake Administration.2003.Technical Specification for Digital Observation of Earthquakes［M］.Beijing：Seismological Press：51-53（in Chinese）.

中国计量科学研究院.1995.GB／T13823.11—1995.振动与冲击传感器的校准方法：激光干涉法低频振动一次校准［S］.北京：中国计量出版社：1-3.

National Institute of Metrology.1995.GB／T13823.11—1995.Methods for the Calibration of Vibration and Shock Pick-ups：Primary Vibration Calibration by Laser Interferometry at Low Frequencies［S］.Beijing：China Metrology Publishing House：1-3（in Chinese）.

International Organization for Standardization of Switzerland.1999.ISO 16063.11—1999.Methods for the Calibration of Vibration and Shock Transducers.PartⅡ：Primary Vibration Calibration by Laser Interferometry［S］.Geneva：Internationel Organization for Standardization：1-2.