一种状态维修适用性的定量分析方法
昝 翔 张仕新 刘艳超李 浩 韩朝帅
(1.装甲兵工程学院技术保障工程系 北京 2.中国人民解放军驻5460厂军事代表室 北京)
随着高新技术的应用,装备的故障规律和故障模式日趋复杂化,定时维修的适用范围逐步减小,使得状态维修(Conditionbased Maintenance,CBM)逐步得到重视和推广。CBM可以充分利用装备的剩余寿命,在保证可靠性的前提下提高装备的可用度。对于装甲装备实现精确保障,减少维修保障费用具有重要的意义。
对装甲装备所有的维修单元进行CBM是不现实的,也没有必要,在确定CBM对象时首要进行适用性性分析。对于装备CBM是否符合CBM的适用条件,有定性分析和定量分析两种方法。定性分析主要是通过设定一些评价因素,对维修单元选取最优的维修方式。定量分析则通过数学方法,寻找维修单元的状态变化是否符合CBM的适用条件。
一、状态维修适用性
1.状态维修基本原理
大部分故障的发生是一个逐渐变化的过程,这个过程可用图1的P-F曲线表示。其中O点为故障萌发点,即状态劣化的实际起点;P点为潜在故障点(Potential Failure),从这点开始异常的状态可以通过现有的技术手段准确的检测;F点为功能故障点(Functional Failure),即装备最终失效的时间点。从P点到F点之间的时间长度称为P-F间隔[1][2]。
CBM的基本原理是当P-F间隔期足够长,在P点和F点之间能够通过一定的手段,检测出装备的故障征兆,并且使用相应的维修措施,预防装备功能故障发生。
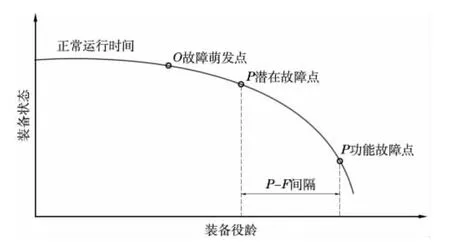
图1 P-F间隔曲线
2.状态维修的适用条件
根据CBM的基本原理,可以得出CBM的适用条件共有两点,(1)必须要有可以检测的潜在故障点。(2)必须要有足够长的P-F间隔期。
3.状态维修的适用性分析原则
在分析装备各维修单元CBM适应性时,是以单元在现有条件下可以监测到的数据为准。有了以上的先决条件,CBM适用性分析时所用的数据时还应该符合3个条件。(1)必须是在现有技术条件下可以采集的数据。(2)采集数据时不能影响装备的正常使用,也不能影响装备的技战术性能。(3)所选数据必须能够长期监测,具有普遍性,即同种类的装甲装备均可以采集到的数据。
二、回归分析方法简介
回归分析,是指在实际问题中,寻找两个或多个变量之间的关系,并利用观测数据拟合系统的数学模型的方法[3]。利用回归分析方法处理数据可分两个步骤。
1.分析数据做出散点图
2.建立数学模型拟合回归曲线
根据对散点图变化趋势的分析,判断数学模型,建立了数学模型之后,需要对函数中的位置参数进行估计。在具体运用时,需要通过变量变换,将非线性问题转化为线性,再利用线性回归的求解步骤进行运算。常见的几种曲线回归模型线性化方法如表 1 所示[4]。
根据文献4,可得线性回归分析求解步骤为:
设随机变量 和可测变量 服从线性关系

则称Y与x服从一元线性回归模型。
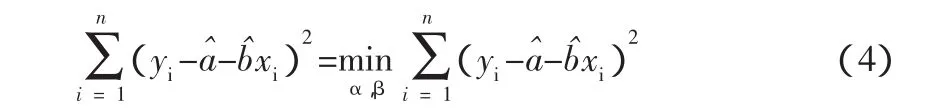
采用微分法求解,即
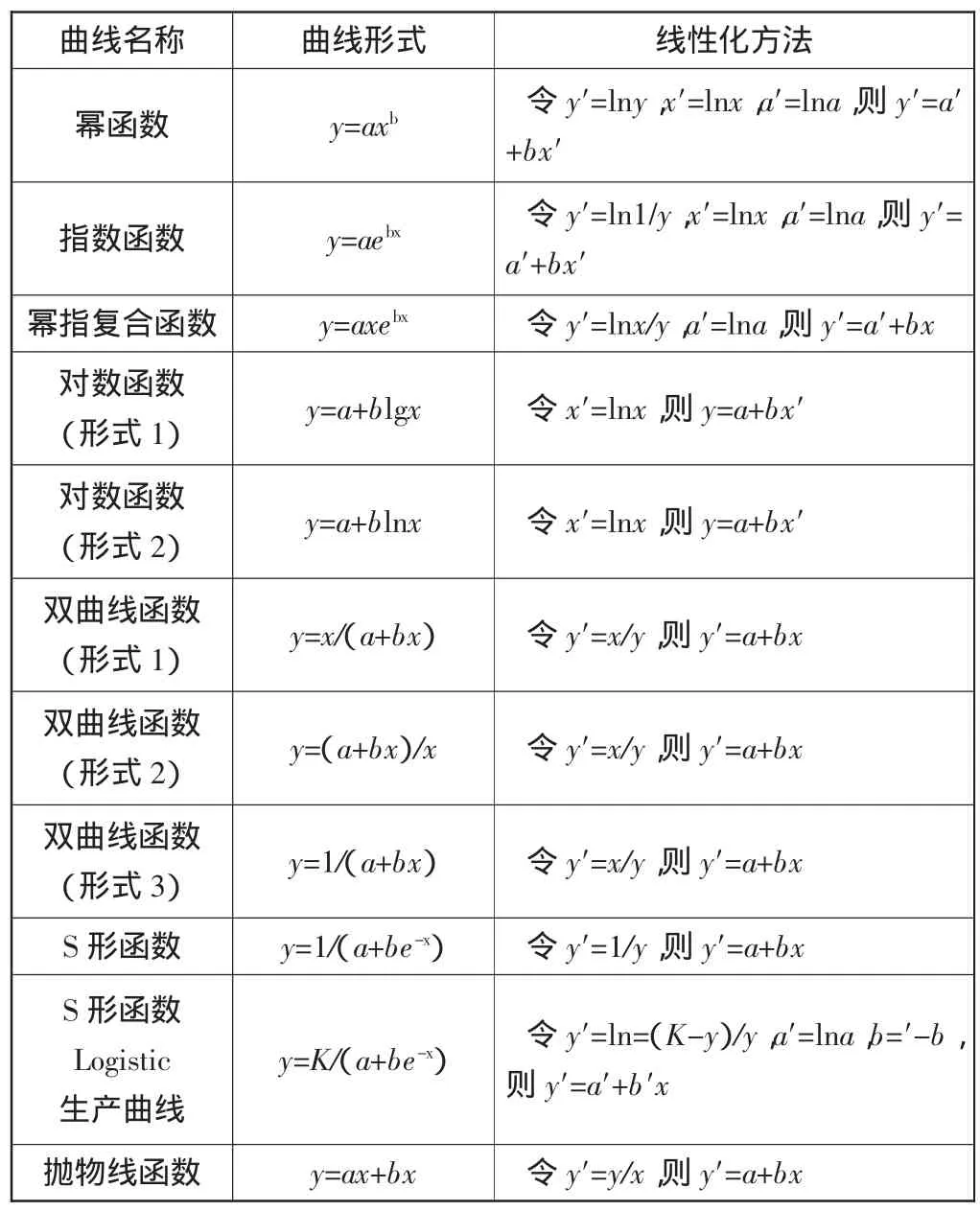
表1 常见曲线回归模型线性化方法
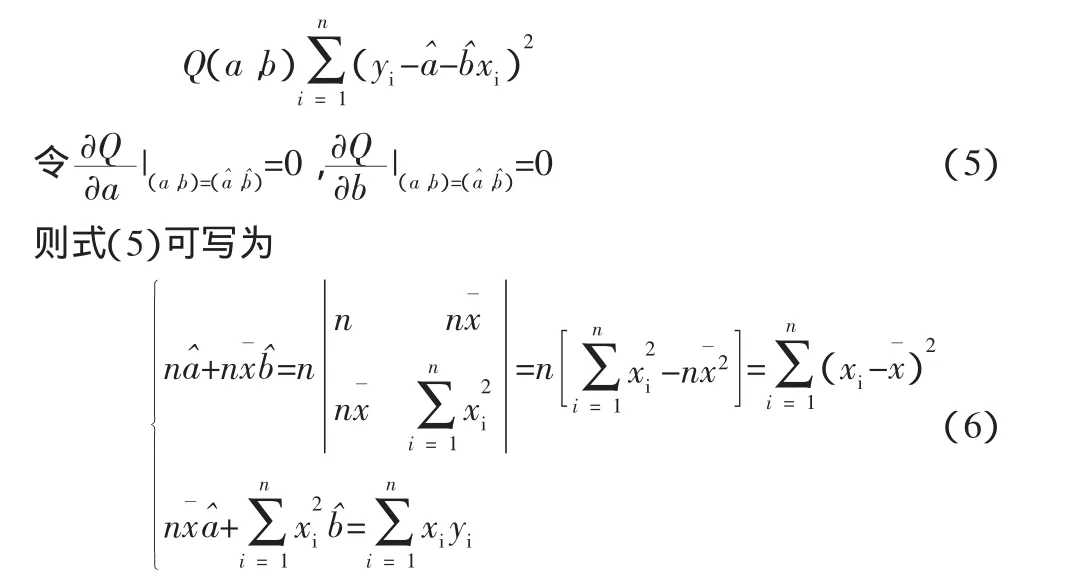

上述公式是针对一组观测值(yi,xi)(1,2,…,n)所做的,当换为(yi,xi)时,可得(a,b)的估计量为
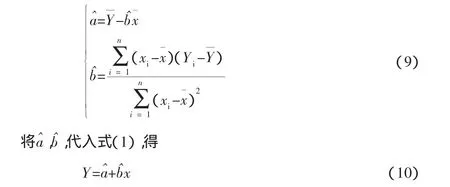
即为Y关于x的线性回归方程。根据表1所示的线性方法,求得原函数。
3.进行检验,确定回归模型
进行回归分析求解了相关函数后,为了检查得出的函数关系是否具有显著性,需要对回归模型进行检验,检验时通常使用3个指标,根据文献3可得:
(1)可决系数R2。可决系数的定义为(11)

(2)相关系数r(13)。对统计量r和ra临界值(查表自由度取n-m-1=n-2)进行比较,判断显著性水平。

(3)显著性(F)检验。对统计量F和临界值Fa(查表自由度取n-2)进行比较,判断显著性水平。通过显著性检验,若得出拟合的函数曲线结果可以接受,则可对该函数进行下一步分析。若判断可能符合变化规律的函数有多个,可分别进行拟合后进行比较,选取最优的拟合结果进行分析。
4.分析回归模型得出结论
对所得的回归模型进行分析,通过设定阈值等方法,判断其是否符合CBM适用条件,得出适用性分析的结论。
三、实例分析
根据适用性分析原则,最终确定通过油液分析进行装备适用性分析。根据相关规定,对装备各维修单元的油液进行长期系统地监测,获得大量的监测数据。对数据进行分析,找出油液的监测参数随时间变化的规律,分析P-F曲线是否符合这一变化规律,就可以判断该维修单元是否符合CBM适用性。
油液中各元素磨粒的含量可以反映维修单元的磨损情况和其他相关信息,因此,可以将监测元素的浓度无量纲化,然后直接作为维修单元的状态值进行分析和研究。

表2 Cu元素浓度变化表
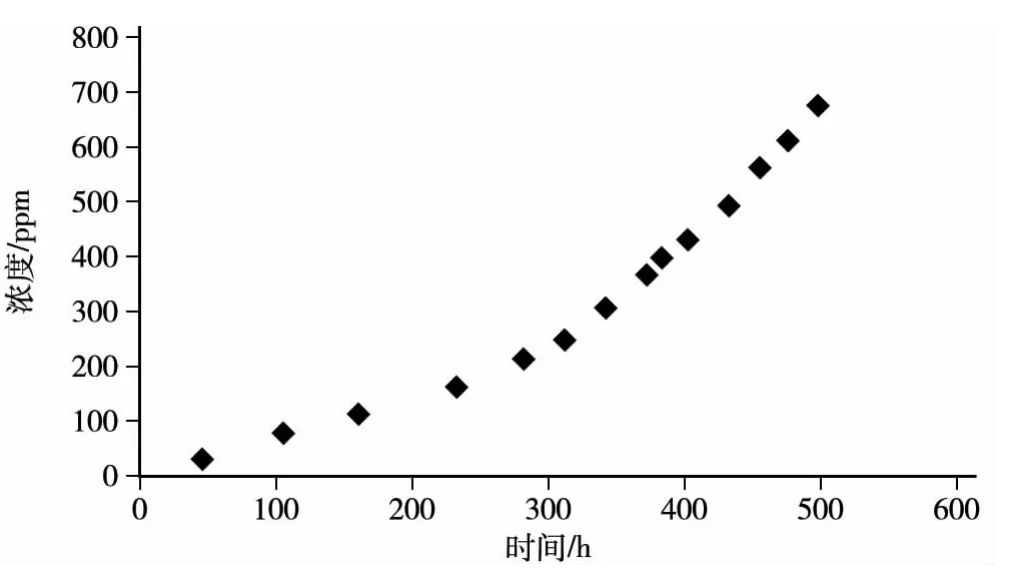
图2 Cu元素浓度变化散点图
以某变速箱油液数据为例进行分析,选取变速箱齿轮油中Cu元素浓度数据(表2)进行研究。
1.整理数据,绘制散点图(图2)
2.根据散点图,判断该浓度变化规律可能符合的函数模型有指数函数分布和幂函数分布
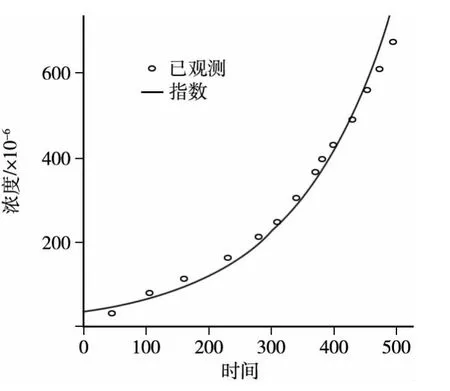
图3 回归分析拟合曲线图
(1)指数函数的数学模型为(14),进行指数函数回归分析,得到的结果如图3所示。回归分析结果汇总见表3。
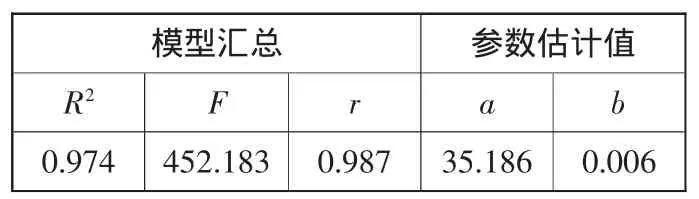
表3 回归分析结果汇总表

(2)幂函数的数学模型为y=axb。进行幂函数回归分析,得到的结果图4和表4。
通过两次回归分析的比较,可得指数函数更符合变化规律,因此采用指数函数拟合结果进行分析。
(3)根据所得的回归分析的结果,可判断该变速箱状态的变化率逐渐上升,可以设定一个斜率的阈值k,当斜率大于该阈值时,就可认为达到潜在故障的P点。因此,可以判断该变速箱符合CBM适用条件,具有良好的适用性。
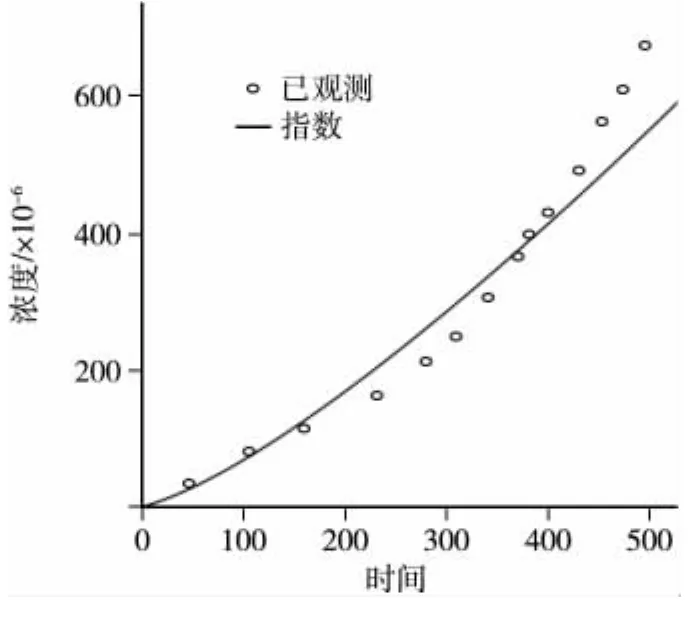
图4 回归分析拟合曲线图
四、结论
通过回归分析,定量地分析了状态维修的适用性。减少了传统定性分析中因主观因素所造成的分析误差。通过实例验证了该方法的有效性,为CBM实施对象的确定提供了适用性分析的依据,同时为CBM的实施打下坚实基础。
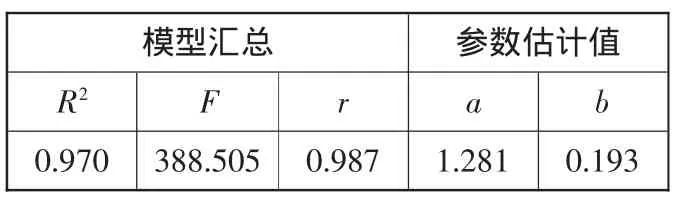
表4 回归分析结果汇总表
1 冯廷敏,杨剑锋,唐静.RCM中潜在故障的净P-F间隔评判与维修策略[J].中国设备工程,2008(8):21-23
2 何江清,王波.军用装备基于状态的维修理论研究[J].舰船电子工程,2009(12):43-44
3 数理统计编写组.数理统计[M].陕西:西北工业大学出版社,1999.7(1):123
4 张建林.MATLAB&Excel定量预测与决策--运作案例精编[M].电子工业出版社.2012:86-87

