全局共享因子的和声搜索算法

刘立群，火久元，王联国

(1.甘肃农业大学信息科学技术学院，兰州 730070;2.兰州交通大学 信息中心，兰州 730070)

和声搜索(harmony search，HS)算法［1-4］是通过类比音乐和最优化问题相似性提出的启发式智能迭代算法。HS算法是对音乐演奏中乐师凭借记忆通过反复调整乐队中各乐器音调，最终达到一个美妙和声状态过程的模拟。研究表明:HS算法是单个体迭代算法，具有迭代速度缓慢、易陷入局部最优以及求解质量不高等缺陷［2-4］。本文针对HS算法音调微调机制中存在随机性更新的缺陷，将全局共享因子［5］的思想引入HS算法，提出一种全局共享因子的和声搜索算法(harmony search algorithm with global sharing factor，GSFHS)。测试函数对比实验表明，GSF-HS算法有效改善了HS算法的优化性能。

1 和声搜索算法思想

随机产生HMS个初始解(和声)放入和声记忆库(harmony memory，HM)内，HMS为和声记忆库的大小，HMCR为和声记忆库取值概率，PAR为音调微调概率，BW为音调微调带宽，Tmax为算法创作的次数，且r1，r2，r∈[0，1]。假设问题是求最小值，其表达形式为:

随机生成 HMS个和声x1，x2…，xHMS放入和声记忆库，形式如下:

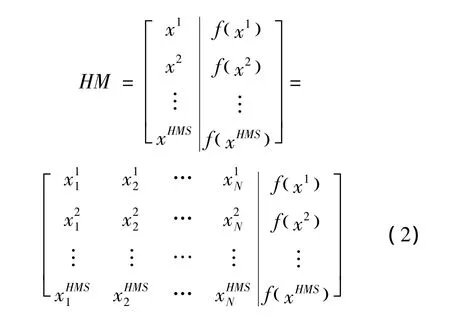
按以下规则生成一个新的和声x'i=(x'1，x'2，…，x'N)。

新和声的每一个音调x'i(i=1，2，…，N)通过学习和声记忆库产生。

如果 r1＜HCMR，则

通过式(3)产生的新和声音调x'i还需进行音调微调。

如果 r2＜PAR，则

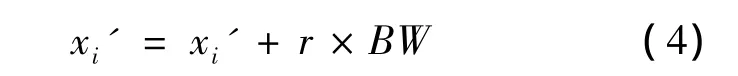
如果r1≥HCMR，则随机选择音调产生新和声x'i，即

对和声记忆库按以下更新策略进行更新。

上述过程不断重复，直至创作(迭代)次数达到Tmax为止。

2 全局共享因子的和声搜索算法

2.1 全局共享因子思想

HS算法音调微调机制利用随机数 r∈[0 ，1]产生新和声。由于这种方式具有随机性，因此对单峰值和多峰值函数寻优问题，HS算法易出现收敛速度慢、精度低等问题。

文献［5］在共享因子［6］基础上提出全局共享因子的概念。全局共享因子αG是仅随迭代次数非线性动态变化的共享因子［5］。由于αG是由较小的初值迅速增大到一个稳态值，故可以抑制随机性音调微调的随机性。

本文将HS算法中创作次数t∈[1，Tmax]应用到全局共享因子中，其表达式为

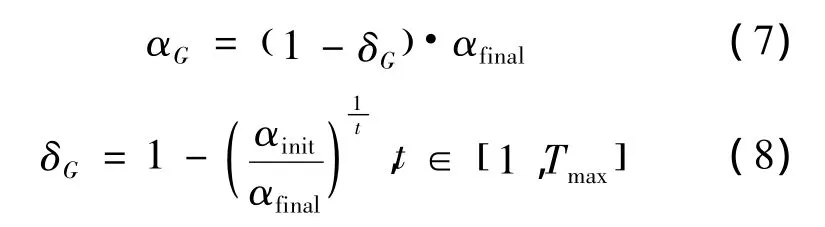
根据全局共享因子理论，在HS算法初期，初始和声随机分布在搜索空间内，为避免和声音调更新步长过大跳过最优个体，应通过较小的全局共享因子减弱音调微调带宽对最差和声的音调微调能力。当迭代次数达到一定程度时，最差和声与通过学习和声记忆库产生的和声的差异如果过小则会出现搜索停滞现象，此时应通过迅速增大到一定值后的全局共享因子增强音调微调能力，实现全局收敛。

2.2 全局共享因子的和声搜索算法

本文将上述全局共享因子αG引入到HS算法中，提出一种全局共享因子的和声搜索算法(harmony search algorithm with global sharing factor，GSF-HS)。

GSF-HS算法是在HS算法基础上对其音调微调机制中的随机性更新进行改进，即GSF-HS算法中音调微调机制按式(9)进行计算，其中全局共享因子αG按式(7)、(8)计算。

GSF-HS算法步骤如下:

步骤1 随机生成HMS个初始和声 x1，x2，…，xHMS，第i个和声记为xi=(x1，x2，…，xN)，其中N为和声音调个数。

步骤2 初始化和声记忆库取值概率HMCR、音调微调概率PAR、音调微调带宽BW和算法创作次数Tmax。

步骤3 选取目标函数f(xi)，按式(2)初始化和声记忆库HM。

步骤4 按式(7)、(8)计算全局共享因子αG。

步骤5 随机生成 r1，r2，r∈[0，1]，如果 r1＜HCMR，则新和声音调x'i按式(3)计算，且若r2＜PAR，则计算出的新和声音调x'i再按(9)式计算;如果r1≥HCMR，则按式(5)计算新和声。按式(6)对和声记忆库进行更新，如此反复迭代直至Tmax为止，输出最优和声。

2.3 算法流程

GSF-HS算法流程见图1。

图1 GSF-HS算法流程

3 对比实验及结果分析

实验采用 Rastrigrin、Griewank、Ackley和Rosenbrock［7-8］4个测试函数作为HS算法的目标函数，分别对HS及GSF-HS算法进行极小值寻优性能测试。其中:Rastrigrin、Griewank、Ackley函数为多峰值函数，Rosenbrock函数为单峰值函数，4个函数的极小值均为0［7-8］。

实验参数设置如下:和声记忆库大小HMS=200，HMCR=0.9，PAR=0.3，BW=0.01，Tmax=30 000。实验所用计算机处理器为Intel Core2，主频为2.0 GHz，内存为2.0 GB，测试平台为VC++6.0。最终测试结果采用独立运行30次后的平均值。

算法性能评价采用如下方法:①固定迭代次数，评价算法收敛精度和速度;② 固定收敛精度，评价算法达到该精度所需的迭代次数。

3.1 固定迭代次数的收敛精度和速度分析

固定迭代次数下，各算法收敛结果如表1所示。4个测试函数在固定迭代次数条件下的函数平均最优值迭代曲线如图2～5所示。

对多峰值 Rastrigrin和 Ackley函数，表1表明:GSF-HS算法平均最优值结果均优于HS算法，且GSF-HS算法标准差较HS算法更具优势，改进算法对这2个函数的收敛精度改善较为明显。图2的Rastrigrin函数和图4的Ackley函数迭代曲线表明:GSF-HS算法收敛速度均优于HS算法。

对多峰值 Griewank函数，表1表明:虽然GSF-HS算法平均最优值结果远优于HS算法，但其标准差较HS算法高，改进算法对Griewank函数的收敛精度没有明显改善。图3的Griewank函数迭代曲线显示:在迭代次数少于10 000时，GSFHS算法的收敛速度优于HS算法，但在之后的迭代中，GSF-HS算法收敛速度并无太大改进。

对单峰值Rosenbrock函数，表1表明:GSF-HS算法平均最优值结果远优于HS算法，且GSF-HS算法标准差为0，明显优于HS算法，改进算法对单峰值函数的收敛精度改善较为明显。图5的Rosenbrock函数迭代曲线显示:在迭代次数超过20 000之后，GSF-HS算法的收敛速度较HS算法有较大提升。

图2 Rastrigrin函数平均最优值迭代曲线

图3 Griewank函数平均最优值迭代曲线

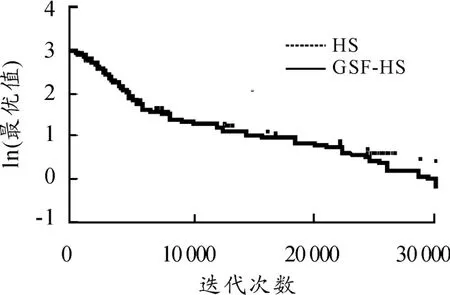
图4 Ackley函数平均最优值迭代曲线

图5 Rosenbrock函数平均最优值迭代曲线

3.2 固定收敛精度下的迭代次数分析

4个测试函数的目标精度和各函数达到目标精度时的平均迭代次数见表2［7-8］。实验结果表明:GSF-HS算法达到目标精度的次数明显少于HS算法。由此可知，GSF-HS算法收敛精度、速度均优于HS算法。

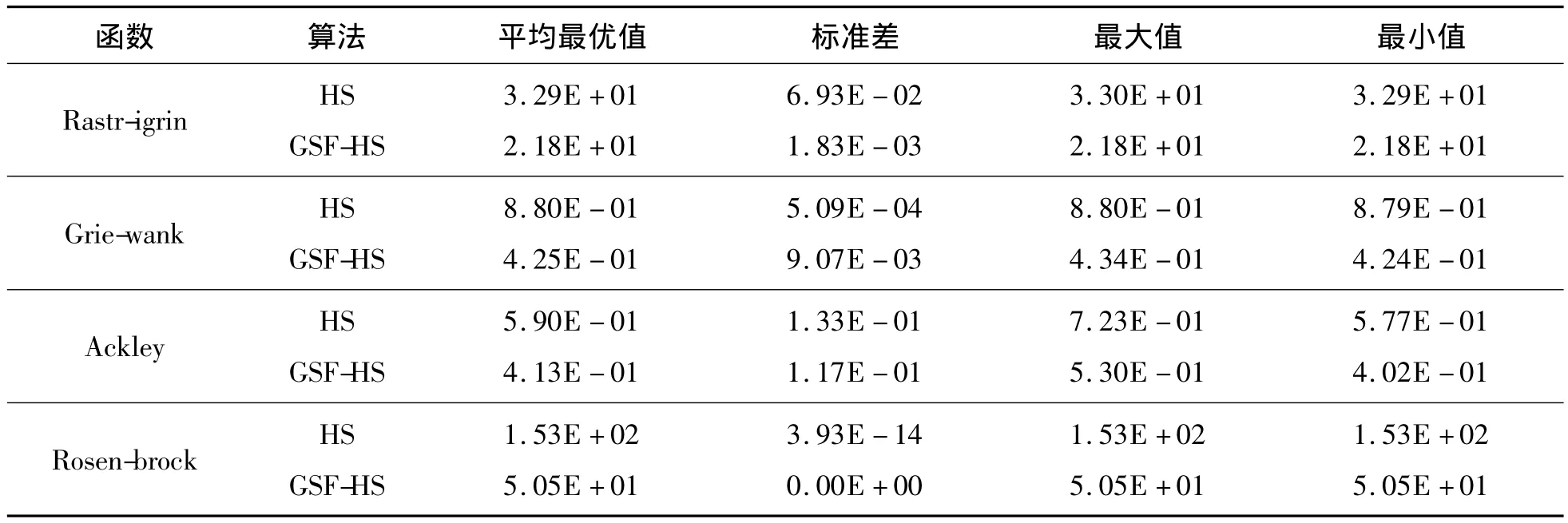
表1 固定迭代次数结果比较

表2 固定收敛精度结果比较

4 结束语

本文提出一种全局共享因子的和声搜索算法，将全局共享因子思想和HS算法创作次数相结合，并将其应用到HS算法的音调微调机制中以改进HS算法音调微调机制随机性更新的缺陷。4个测试函数的对比实验结果表明:GSF-HS算法收敛精度、速度均优于HS算法，有效改善了HS算法的优化性能。

［1］Geem Z W，Kim J H，Loganathan G V.A new heuristic optimization algorithm:harmony search［J］.Simulation，2001，76(2):60-68.

［2］赵鹏军，刘三阳.一种新的智能优化及其改进研究［J］.小型微型计算机系统，2010，31(5):955-958.

［3］雍龙泉.和声搜索算法研究进展［J］.计算机系统应用，2011，20(7):244-248.

［4］韩红燕，潘全科，梁静.改进的和声搜索算法在函数优化中的应用［J］.计算机工程，2010，36(13):245-247.

［5］刘立群，王联国，韩俊英，等.基于全局共享因子的混合蛙跳算法［J］.计算机工程，2013，39(10):162-166.

［6］王辉.一种带共享因子的人工蜂群算法［J］.计算机工程，2011，37(22):139-142.

［7］王凌.智能优化算法及其应用［M］.北京:清华大学出版社，2001:2-6.

［8］Andrice P，Engelbrecht.Fundamentals of Computational Swarm Intelligence［M］.谭营，译.北京:清华大学出版社，2009:10-15.