求解KdV方程和mKdV方程的新方法:(g'/g2)展开法
王思源,陈 浩
(华南师范大学物理与电信工程学院,广州510006)
非线性方程的求解是自然科学,尤其是非线性科学中最重要的部分.可用来阐述诸多复杂现象,例如规范场理论和量子场论中的磁单极子问题、瞬子问题;固体物理中的极化子问题和铁磁链孤波问题;流体力学中的水波问题等.近年来,非线性方程的研究热点是寻找新的解法并且得出新的精确解. 一些比较主流的求解方法开始在非线性方程中扮演重要角色,例如Hirota 双线性展开法[1]、Jacobi 双曲函数展开法[2]、齐次平衡法[3]及(g'/g)展开法等[4].
(g'/g)展开法由Wang 等[4]于2008年首先提出,并得出了KdV 方程和mKdV 方程的精确解以及孤立波解.但是,这种方法存在推导繁琐、冗长等缺点.接着,Li 等[5]提出了(ω/g)展开法并且利用(g'/g)和(g'/g2)这2 种展开方法求得了Vakhnenko 方程的精确解.陈继培等[6]用(g'/g2)展开法求出了非线性Klein-Gordon 方程的精确通解.使方法比前一种方法更加简便、有效. 这也同样适用于KdV 方程和mKdV 方程的求解.
本文引入并介绍(g'/g2)展开法的原理及求解过程,研究了KdV 方程和mKdV 方程的行波解.
1 (g'/g2)展开法的主要求解步骤
(g'/g2)展开法的主要求解步骤[5-6]如下:
第1 步 假设含独立变量x、t 的非线性方程可以表示为

其中u=u(x,t).
第2 步 对式(1)做行波变换u=u(ξ),ξ=x-Vt,得

第3 步 假定式(2)的解可以表示为
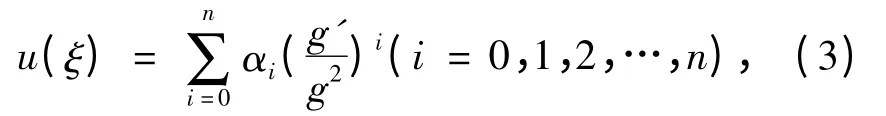
式中,g=g(ξ)满足二阶线性常微分方程

式中αi,a,b 是待定常数,αi≠0,n 可以根据其次平衡法确定.
第4 步 将方程(4)根据不同条件求解,代入式(3),合并的同类项.令各项系数为0,得出并求解关于αi,a,b 的方程组.
第5 步 把第4 步得出的解代入式(3),可得非线性方程的精确行波解. 此步可通过相关数学软件(如Mathematica 或Matlab)完成.
2 (g'/g2)方程的求解过程
将方程(4)变形,得到

取g=1/y,于是上式可以写为

当ab >0 时,

当ab <0 时,

于是可得方程(4)的通解:
(1)当ab >0 时,

(2)当ab <0 时,
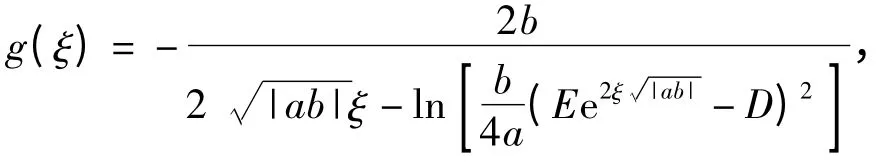

上式也可以改写为

(3)如果a=0,b≠0,则

3 KdV 方程的精确行波解
KdV 方程为

是非线性物理问题中的重要方程,主要用于研究浅水波问题和离子声波问题,并受到学界关注[7-8].对式(5)作行波变换u=u(ξ),ξ=x-Vt,得到

上式对ξ 积分,并取积分常数为C,有

根据齐次平衡法,式(3)中n =2(n +3 =2n +1).因此KdV 方程的解可以写为

利用式(3)和方程(4),可得
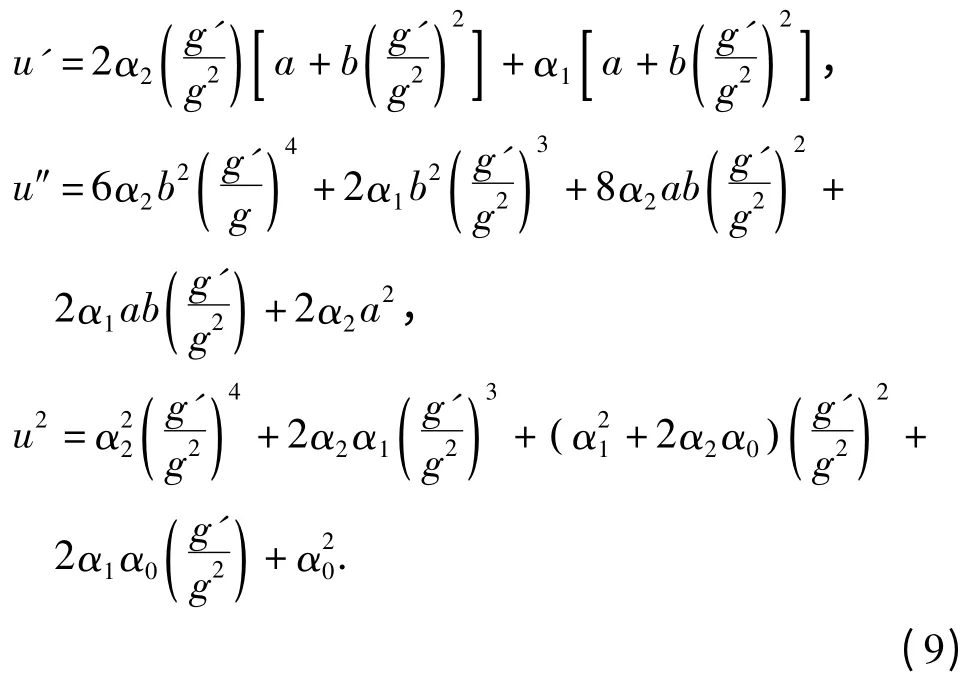


求解以上方程组,可以得到
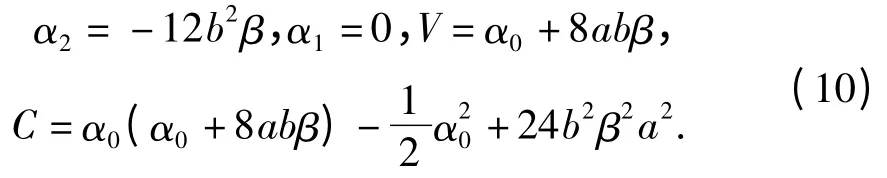
利用式(10)、(8)可以写为

把式(8)的通解代入式(11),可得到KdV 方程的精确通解.
(1)当ab <0 时,得到双曲函数通解

其中E,D 是任意常数,ξ=x-(α0+8abβ)t.
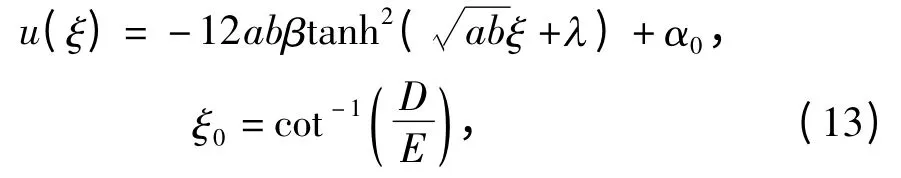
即KdV 方程的孤立波解.
(2)当ab >0 时,

其中E,D 是任意常数,ξ=x-(α0+8abβ)t.

即KdV 方程的三角函数解,反之亦然.
(3)当a=0,b≠0 时,

其中E,D 是任意常数,ξ=x-(α0+8abβ)t.
4 mKdV 方程的精确通解
mKdV 的表达式为

作行波变换u=u(ξ),ξ=x-Vt,式(17)可得

上式对ξ 积分,并取积分常数为C,得到

根据齐次平衡法,在式(3)中,n=1(3n +1 =n +3).则式(19)存在以下解

利用式(3),可得

把式(21)、(22)代入式(20)得到:

由以上方程有

(1)当ab <0 时,双曲函数通解为


即mKdV 方程的孤立波解.
(2)当ab >0 时,三角函数通解为

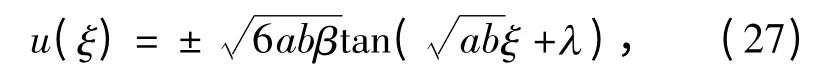
即mKdV 方程的三角函数解.
(3)当a=0,b≠0 时,有

此处E、D 可取任意常数.
5 (g'/g2)展开法与其他方法求解行波解的比较
一般来说,求解KdV 方程和mKdV 方程的方法主要是利用椭圆函数的性质. 然而,椭圆函数法求解上述2个方程时,得到的是相关的椭圆函数正弦波解或余弦波解,这介乎2个极限:线性解和孤立波解之间,在得到椭圆函数解之后,还需要选取适当的极限才能得到对应的孤立波解. 另外,根据相关文献[4],(g'/g)展开法也是一个求解方程的较好方法,但是在求解过程中不具有用(g'/g2)展开法所体现的优势.
6 结论
通常,求解KdV 方程和mKdV 方程的方法主要是利用椭圆函数法.然而,椭圆函数法求解上述2个方程时,得到的是相关的椭圆函数正弦波解或余弦波解,这介乎2个极限:线性解和孤立波解. 在得到椭圆函数解之后,还需要选取适当的极限才可以得到对应的孤立波解. 另外,采用(g'/g)展开法求解过程比较冗长、繁琐.
本文采用(g'/g2)展开法研究了KdV 方程及其变形mKdV 方程. 并且得出了这2个方程的精确通解:双曲函数解、三角函数解及有理函数解. 如果双曲函数中的常数做出适当改变,可得到孤立波解.根据求解过程,相比(g'/g)展开等方法,采用(g'/g2)展开法研究非线性方程(KdV 方程和mKdV 方程),具有计算简便、直接等优点. 至于(g'/g2)展开法在求解其他非线性方程的应用有待研究与讨论.
[1]Hirota R. Exact solution of the Kortewegde Vries equation for multiple collisions of solitons[J]. Physical Review Letters,1971,27:1192-1194.
[2]Liu S K,Liu S D,Fu Z T,et al. Jacobi elliptic function expansion method and periodic wave solutions of nonlinear wave equations[J]. Physics Letters A,2001,289:69-74.
[3]Wang M L. Solitary wave solutions for variant Boussinesq equations[J].Physics Letters A,1995,199:169-172.
[4]Wang M L,Li X Z,Zhang J L. The (g'/g)-expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics[J]. Physics Letters A,2008,372:417-423.
[5]Li W A,Chen H,Zhang G C. The (ω/g)-expansion method and its application to Vakhnenko equation[J].Chinese Physics B,2009,18(2):400-404.
[6]陈继培,陈浩. (g'/g2)展开法及其在耦合非线性Klein-Gordon 方程中的应用[J]. 华南师范大学学报:自然科学版,2012,44(2):63-66.Chen J P,Chen H. The (g'/g2)-Expansion method and its application to coupled nonlinear Klein-Gordon Equation[J]. Journal of South China Normal University:Natural Science Edition,2012,44(2):63-66.
[7]Feng Z S,Chen G. Solitary wave solutions of the compound Burgers Korteg-de Vries Equation[J].Physica A,2005,352:419-435.
[8]蒋毅,陈渝芝,蒲志林.1 +1 维空间中变系数KdV 方程组的精确解[J]. 四川师范大学学报:自然科学版,2007,30(6):670-673.Jiang Y,Chen Y Z,Pu Z L. Explicit solutions to the {1+1}-dimensional KdV Equations with variable coefficients[J]. Journal of Sichuan Normal University:Natural Science,2007,30(6):670-673.

