基于多尺度粗糙集模型的决策树在高校就业数据分析中的应用
麦晓冬 ,贾 萍,翁建荣,彭凌西
(1.广东轻工职业技术学院电子通信工程系,广州510300;2.广东轻工职业技术学院实训实验中心,广州510300;3.广州大学计算机科学与教育软件学院,广州510006)
目前,积累在高校学生管理信息系统里面的海量数据尤其是历史就业数据,没有得到应有的重视.按照《国家中长期教育改革和发展规划纲要(2010—2020年)》[1]对教育信息化建设提出的目标:“整合各级各类教育管理资源,为宏观决策提供科学依据”,分析历史就业数据,挖掘出影响就业的主要因素,为决策者改进学校就业指导工作、提高就业率和就业质量提供决策支持.
对就业数据进行分析主要是希望找出数据背后隐藏着的一些重要的模式和知识.近年来,有学者提出把数据挖掘应用到该问题中,主要是将决策树这种应用广泛的数据挖掘分类方法应用到实际的决策分类问题中.文献[2]、[3]采用了C4.5 算法进行决策分类树的生成,该算法是由Quinlan 研制的国际上最早和最有影响的ID3 决策树生成算法[4]的改进算法,但该方法不能很好地处理就业数据中存在的模糊性和不确定问题;文献[5]采用的模糊决策树算法[6]是对传统决策树的扩充和完善,使得决策树学习的应用范围扩大到了能处理数据的不确定性;文献[7]提出基于变精度粗糙集算法[8]的决策树模型,从而解决了就业数据中不一致信息的处理.由于实际就业情况的多样性和复杂性,学校历史就业数据一般都是噪声比较大的数据集,而且各级机构对决策精度的要求也有所区别,上述方法在处理决策精度需求不同和噪声适应能力等问题上均无法很好的解决,而基于多尺度粗糙集模型的决策树算法,借鉴了变精度粗糙集的思想,将多尺度概念引入粗糙集理论中,可以很好地解决此问题[9]. 基于此,文中提出将基于多尺度粗糙集模型的决策树算法应用于高校就业数据分析,并以实际就业数据为例进行分析,同时将分析结果与C4.5 算法和基于粗糙集的决策树生成算法的分析结果进行比较.
1 基于多尺度粗糙集模型(MRSM)的决策树生成算法
基于多尺度粗糙集模型(MRSM)的决策树生成算法是在变精度粗糙集理论的基础上结合尺度变量和尺度函数,利用变量在不同尺度中呈现不同决策规则的特点,生成决策树.
要构建多尺度粗糙集决策树,首先要选择每个节点处的分类属性. 如果选择某一分类属性对节点处样本数据进行分类,它能为决策规则提供最多的确定信息,那么就可以选择它作为分类属性.由于近似边界域的存在,信息的确定性会出现某种程度上的近似包含问题,即不确定的信息也可能会提供有用的决策规则[10]. 文献[9]提出的MRSM 算法,定义了近似分类精度dci(D)来界定这种近似包含的范围,近似分类属性值越大,可以为决策分析提供更多的确定信息和一些可能起作用的不确定信息部分,因此选择近似分类精度最大的属性作为根节点的扩展属性.
设多尺度决策信息系统S = (U,C ∪D,V,f(s)),全域U,条件属性集C,决策属性集D,决策函数f(s),Ci为C 的一个条件属性,{X1,X2,…,Xn}是Ci在全域U 的一个子域,{Y1,Y2,…,Yn}是决策属性D 在全域U 的一个子域,条件属性Ci对决策属性D 关于决策函数f(s)的近似分类精度为dci(D).
近似分类精度的计算公式如下:
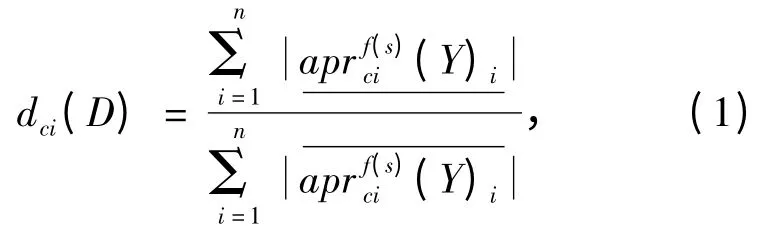
在具体生成决策树的过程中,通过引入抑制因子在决策树生成过程中对决策树进行修剪,可以减少决策树生成后还需要剪枝的步骤,提高了决策树生成的速度.同时,生成出来的决策树没那么复杂,也便于决策者理解.
文献[9]给出的抑制因子的定义为:对决策表信息系统S=(U,C,D,V,f),C 和D 分别称为条件属性集和决策属性集,分类U/C ={x1,x2,…,xn},U/D ={y1,y2,…,ym},决策规则为rij:des(xi)⇒des(yi).
设kij为决策规则rij的可能性因子,kij=且0≤kij≤1,其中是满足决策规则xi→yj的总样本条数是满足决策规则的前件的样本数.
从抑制因子的定义可知,若全域U 的抑制因子大于某一个给定的阈值λ(0 <λ ≤1),则说明某个决策规则前往取值des(Xi)=f(a,Xi)(aC)时至少有100 λ%的实例在决策属性上取相同的值D0,这时,保留条件属性值f(a,Xi),不再需要往下生成决策树,并直接用D0标记叶子,这样屏蔽了少数噪声数据对决策树造成的不良影响,减少生成的决策树的复杂度[9].
由上述分析,给出基于多尺度粗糙集模型的决策树生成算法:
输入:多尺度决策信息系统S =(U,C∪D,V,f(s)),对象集U,条件属性集C,决策属性集D,决策函数f(s),阈值λ(λ >0.5);
输出:一棵决策树.
Step1:生成一个节点N;
Step2:计算出每个条件属性C 对应决策属性D关于尺度函数f(s)的近似分类精度dci(D),并选取其最大值对应的条件属性值来标记其根节点N,若存在dci(D)值相同的情况,则选取对应的等价类最小的那个值;
Step3:如果dci(D)≥f(s),则转到Step4,否则转到Step6;
Step4:计算出当前条件属性C 对应的可能性因子kij和抑制因子yci(Xi)的值,并转到Step5;
Step5:根据计算出的抑制因子yci(Xi)的值与阈值λ 进行对比,若yci(Xi)≥λ,则保留当前条件属性值f(a,Xi)用D0标记叶子节点,并结束该子集的计算;若yci(Xi)<λ,则选取条件属性值为f(a,Xi)时划分的子集作为新的对象集,并返回Step2;
Step6:根据选择的条件属性节点将对象集分成若干个子集,并计算子集所对应的决策属性值,如果属性值相同,则直接用决策属性值标记叶子节点,结束该子集的计算,直到所有子集运算结束;否则选取这些子集作为新的对象集,返回Step2.
2 基于MRSM 的决策树生成算法在就业数据分析中的应用
2.1 数据收集及处理
对就业数据进行挖掘分析,首先要有明确的数据分析对象.本文的数据选自某学院2012 届毕业生的数据,抽取出与就业有关的属性,如性别、专业成绩、外语等级、计算机等级、技能等级和就业单位等,并取其中20 条实例作为就业训练样本集,条件属性集为C={e1,e2,e3,e4},决策属性为D=(d),如表1所示[11].其中条件属性专业成绩e1根据学生专业成绩的加权平均分并分成3 类:中等(加权平均分<70)、良好(70≤加权平均分<85)、优秀(加权平均分≥85 分),并分别取值(1 表示中等,2 表示良好,3 表示优秀),外语等级e2根据学生考取的英语证书等级取值(1 表示A 级,2 表示四级,3 表示六级),计算机等级e3根据学生考取的计算机证书等级取值(1 表示1 级,2 表示2 级),技能等级e4根据学生考取的技能证书等级取值(1 表示初级,2 表示中级,3 表示高级).对于决策属性就业单位d,首先根据学生就业单位的单位性质将就业单位分成事业单位(A)、民营企业(B)、外资企业(C)三类,事业单位大体上包括政府单位、国有企业、大中专院校等,民营企业大体上包括民间个人或组织经营的企业,外资企业大体上包括外国独资或中外合资的企业,并按各类企业所提供的待遇效益、地理位置等进行梯队划分,量化取值为好事业单位(A1)、一般事业单位(A2)、好民营企业(B1)、一般民营企业(B2)、好外资企业(C1)、一般外资企业(C2). 数据量化后的结果见表1.
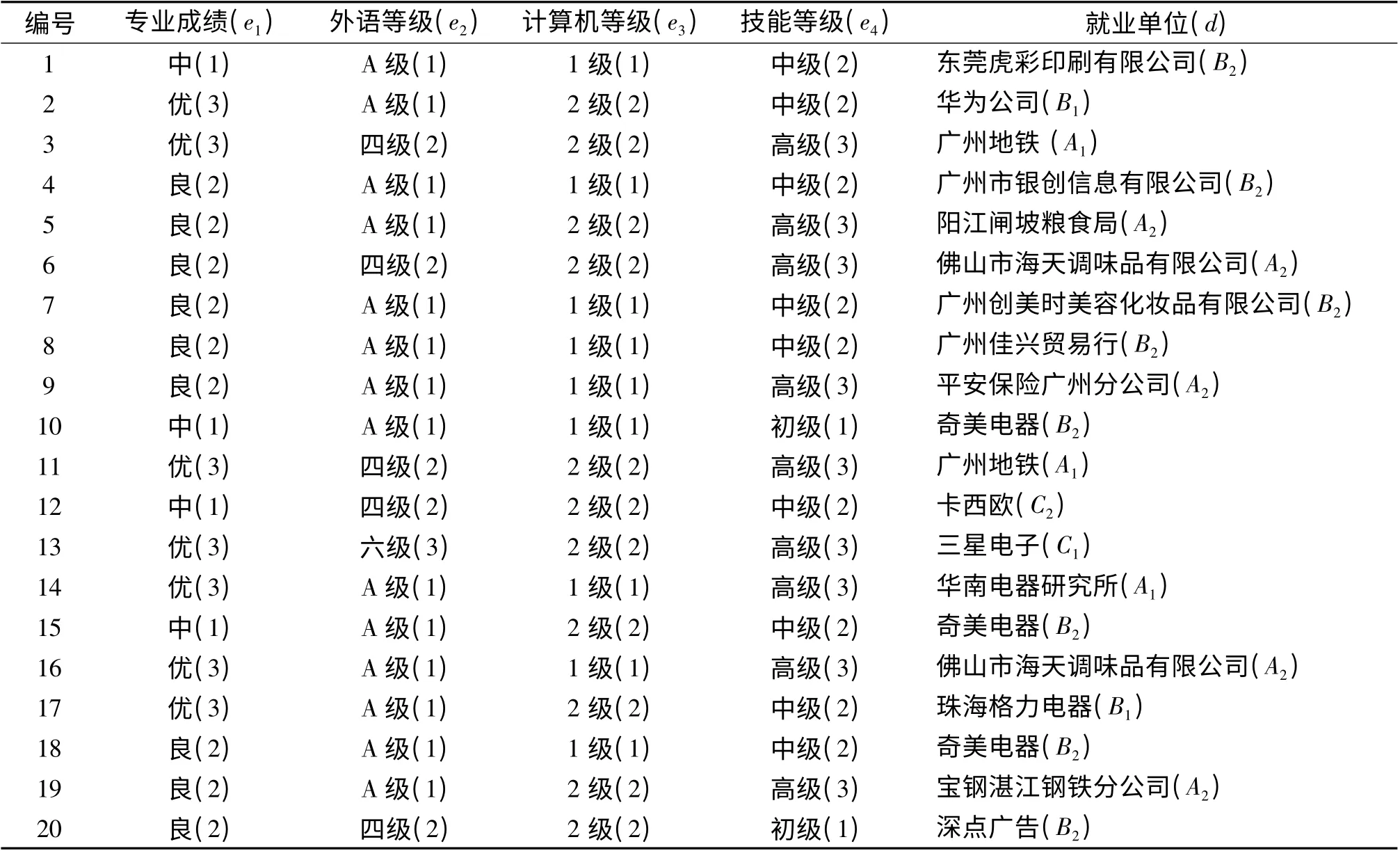
表1 学生就业数据Table 1 The employment data of students
2.2 构造决策树
根据上述给出的基于MRSM 的决策树生成算法,我们首先设定尺度函数f(s)=0.6 和阈值λ =0.8,用该算法构造决策树过程如下:
(1)根据式(1)计算每个条件属性相对决策属性关于尺度函数f(s)的近似精度,得到de1(D)=0.74,de2(D)=0.15,de3(D)=0.32,de4(D)=0.32.
(2)根据算法Step2,选取属性e1即专业成绩标记为根节点e1.
(3)de1(D)=0.74≥0.6,所以转到算法Step4.
(4)由属性e1有3 种可能值(1,2,3)可知形成的树有3个不同分支,其中在e1=1 的情况,得到抑制因子的值为1 >λ,因此将属性e1标识为叶子;在e1=2 和e1=3 的2 种情况中,得到的抑制因子的值不满足yci(Xi)≥λ 的条件,则取当前子集返回Step2进行计算.
(5)再次根据式(1)计算近似精度值,得出de4=1 的值最大,因此选择属性即技能等级为树的节点.以此类推,最终得到1个复杂度为8、深度为3和叶子数为5 的决策树(图1).
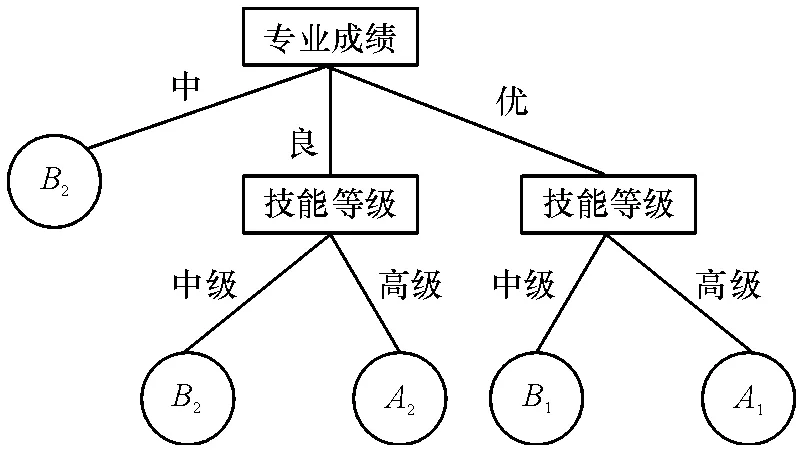
图1 f(s)=0.6 时生成的决策树Figure 1 Generated decision tree of f(s)=0.6
MRSM 决策树生成算法可基于不同的尺度函数f(s)获得不同角度、不同尺度的决策树,因此,我们分别再取f(s)=0.8 进行计算分析.完成如上运算过程后,得到一棵复杂度为10、深度为3、叶子数为6 的决策树(图2).
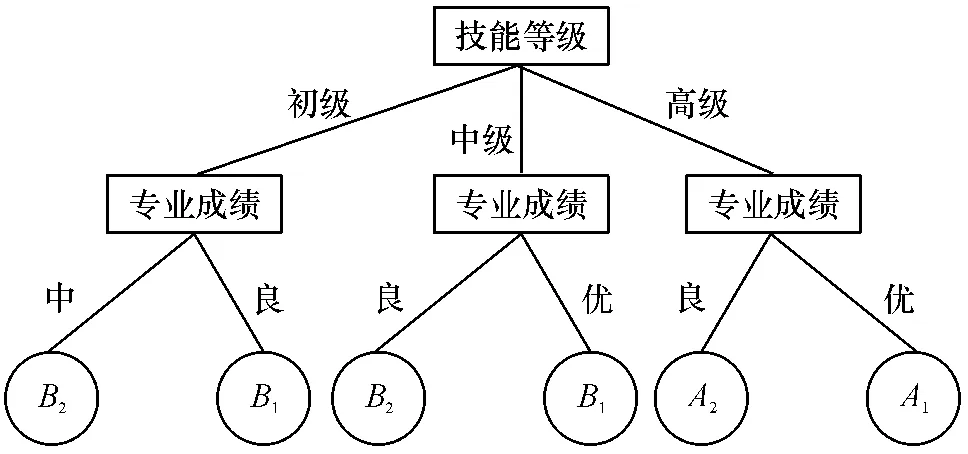
图2 f(s)=0.8 时生成的决策树Figure 2 Generated decision tree of f(s)=0.8
2.3 尺度的讨论
分析本文实验结果,随着尺度变量的增加,f(s)变大,对知识的表达就更详细,决策规则的数目逐渐变多,但是生成的决策树结构的复杂度也越高.这是因为在MRSM 决策树生成算法中,由于尺度变量增加,决策属性所对应的近似边界的范围会逐渐变窄,决策规则的覆盖度提高. 但是,要说明的是,在噪声较多的情况下,决策规则的覆盖度提高有时候得出的一些规则是一些不确定的规则[10]. 所以,要充分考虑不同用户对决策精度的要求,尺度函数f(s)参数的选择,要根据决策分析时面对的数据集和用户对研究问题的精确程度,合理选择参数.
2.4 规则知识描述
根据基于MSRM 的决策树生成算法,从根节点到叶子节点可得到一条决策规则. 结合本文就业训练集进行分析的结果,通过图1 可以得出当f(s)=0.6 时的决策规则:
Rules1:If 专业成绩=“中”then 在一般民企就业;
Rules2:If 专业成绩=“良”and 技能等级=“中级”then 在一般民企单位就业;
Rules3:If 专业成绩=“良”and 技能等级=“高级”then 在一般事业单位就业;
Rules4:If 专业成绩=“优”and 技能等级=“中”then 在好的民企单位就业;
Rules5:If 专业成绩=“优”and 技能等级=“高级”then 在好的事业单位就业.
通过图2 也可以得出在决策函数f(s)=0.8 时的决策规则,在这里不再详细列出具体规则.
由以上2 种决策函数不同取值所得出的规则分析,要提高毕业生的就业质量,都应该在人才培养方案中加大对学生的专业素养的培养,专业课程的设置必须贴近工作实际;针对毕业生就业方向主要集中的民营单位和事业单位,学生应该要考取更高级的技能证书,尤其是事业单位更加认可的等级证书.
2.5 结果与分析
为验证基于MRSM 决策树生成算法对就业数据挖掘的有效性,采用实验环境如下:硬件:Intel(R)Core(TM)2 Duo CPU 2.93 GHz,2G 内存;软件:Windows XP(SP3)和Matlab 6.5. 实验训练集为表1 的就业数据,将本算法与C4.5 和基于粗糙集(Rough Set)的决策树生成算法[12]进行比较,其结果如表2所示.可见,采用基于多尺度粗糙集模型的决策树生成算法对就业数据进行分析,树形结构的规模和深度都不大,所以产生的规则数量也比较简洁,但不存在不可分的数据集. 而其他2 种算法对就业数据进行分析,得出的决策树相对复杂,产生的规则数目较多,且存在不可预测的数据集.
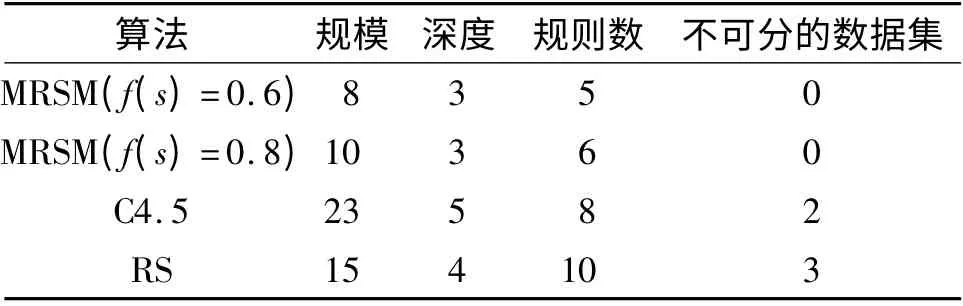
表2 不同算法生成决策树的比较Table 2 Comparison of decision trees generated by different algorithms
3 基于MRSM 的决策树生成算法的性能评价
评价每一种决策树生成算法的性能,决策树的复杂度和分类准确度是2个比较重要的因素. 复杂度是指根据分类发现模型对问题的规则描述的简洁性和运算复杂性,规则描述越简洁就越容易理解,如决策树的规模和深度以及运算耗时等指标;分类准确度是指根据所得的分类模型准确预测新的或未知的数据类的能力,准确度高意味着可以在处理巨量数据时可以得到更精准的分类数据[13].
按决策树运用的2个阶段:学习阶段和测试阶段,实验选取1 000 条就业数据作为测试集,对上述利用训练集建立的决策树模型进行测试实验,即运用生成的决策模型对输入的测试集数据进行分类.实验按不同尺度函数f(s)=0.6 和f(s)=0.8 分别进行实验,从决策树的分类准确度和运行时间这2个决策树性能方面将本算法与C4.5 以及RS 算法进行了比较,实验比较结果见表3. 结果显示,基于多尺度粗糙集模型的决策树生成算法在分类准确度和运行速度上都优于C4.5 算法,虽然在不同尺度函数取值情况下其分类准确度要低于或等于RS 算法的分类准确度,但在运行速度上都要优于对方.需要注明,实验样本集数据会对决策树性能产生影响,且结合上文分析得知,基于多尺度粗糙集模型的决策树生成算法中尺度函数的取值也对决策树性能具有重要的影响. 因此,在进行决策分析时应该根据数据集和用户对研究问题的精确程度,注重参数的选择.
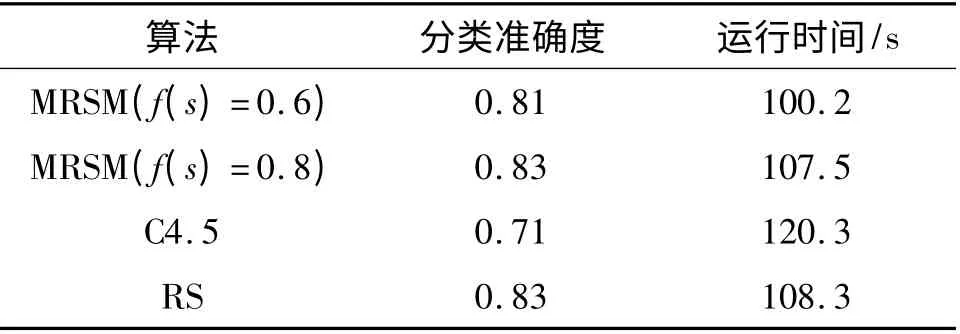
表3 不同算法决策树性能的比较Table 3 Comparison of decision tree performance by different algorithms
4 结语
当前,就业形势日趋严峻,高校应该加大整合资源、提高科学决策工作的力度,依靠科学手段,有效地提高本校毕业生的就业率和就业质量. 本文提出了将基于多尺度粗糙集模型的决策树算法运用到对高校就业数据的挖掘分析,以此挖掘出海量就业数据背后有用的模式和知识. 基于多尺度粗糙集模型的决策树算法,引入了尺度变量和尺度函数,使得生成的决策树能够满足不同用户对决策精度的需求,并使用抑制因子对决策树进行修剪,使得生成的决策树结构简单,决策规则易于理解.将基于多尺度粗糙集模型的决策树算法应用到高校就业数据分析,挖掘出来的规则可以满足学校不同决策者的精度需求,可以有效地帮助学校各级管理层对学校的各项就业工作、人才培养方案的制订等方面提供更准确科学的决策.
[1]国家中长期教育改革和发展规划纲要工作小组办公室. 国家中长期教育改革和发展规划纲要(2010~2020年)[EB/OL]. (2010- 07- 29)[2013- 10-16]. http://www. moe. gov. cn/publicfiles/business/htmlfiles/moe/A01_zcwj/201008/xxgk_93785.html.
[2]雷松泽,郝艳.基于决策树的就业数据挖掘[J].西安工业学院学报,2005(5):24-27.Lei S Z,Hao Y.Data mining in employment based on decision tree[J]. Journal of Xi'an Institute of Technology,2005(5):24-27.
[3]Quinlan J R. Induction of decision trees[J]. Machine Learning,1986,1(1):81-106.
[4]韩晓颖.基于决策树的数据挖掘技术在学生就业指导中的应用[J]. 科协论坛:下半月,2011(12):172-173.Han X Y. Based on the decision tree data mining technology in the students career guidance[J].Science & Technology Association Forum:Second half,2011(12):172-173.
[5]杨断利,张锐,王文显.基于模糊决策树的高校就业数据挖掘研究[J].河北农业大学学报,2012(2):111-114.Yang D L,Zhang R,Wang W X.Data mining in student’s employment base on fuzzy decision tree[J]. Journal of Agricultural University of Hebei,2012(2):111-114.
[6]Janikow C Z. Fuzzy decision trees:Issues and methods[J].IEEE Transactions on Systems,Man,and Cybernetics:Part B,1998,28(1):1-14.
[7]常志玲,王岚. 一种新的决策树模型在就业分析中的应用[J].计算机工程与科学,2011(5):141-145.Chang Z L,Wang L.Data mining in employment based on a new decision tree [J]. Computer Engineering & Science,2011(5):141-145.
[8]孙士保,秦克云. 变精度覆盖粗糙集模型的推广研究[J].计算机科学,2008(11):210-213.Sun S B,Qin K Y. On the generalization of variable precision covering rough set model[J]. Computer Science,2008(11):210-213.
[9]陈家俊,苏守宝,徐华丽.基于多尺度粗糙集模型的决策树优化算法[J]. 计算机应用,2011(12):3243-3246.Chen J J,Su S B,Xu H L. Decision tree optimization algorithm based on multiscale rough set model[J]. Journal of Computer Application,2011(12):3243-3246.
[10]翟敬梅,刘海涛,徐晓.面向噪声数据的多尺度粗糙集模型研究[J].计算机工程与应用,2011(6):12-14;18.Zhai J M,Liu H T,Xu X. Research of multiscale rough set model for noise data[J]. Computer Engineering and Applications,2011(6):12-14;18.
[11]邓自洋.改进决策树算法在高校就业管理中的应用研究[D].上海:华东理工大学,2013.Deng Z Y.An improved decision tree algorithm and its application on university employment management[D].Shanghai:East China University of Science and Technology,2013.
[12]常志玲,周庆敏,杨清莲.基于粗糙集理论的决策树构造算法[J]. 南京工业大学学报:自然科学版,2005(4):80-83.Chang Z L,Zhou Q M,Yang Q L. Decision tree algorithm based on rough set[J]. Journal of Nanjing University of Technology,2005(4):80-83.
[13]丁苗. 决策树技术在毕业生就业数据中的应用研究[D].吉林:辽宁工程技术大学,2012.Ding M.Research on the decision tree applied in the employment data of undergraduate student[D]. Jilin:Liaoning Technology University,2012.

