南京地区低电离层加热效应的初步模拟

孟兴，方涵先

解放军理工大学气象海洋学院，南京 211101

1 引言

“卢森堡效应”被发现以来，科学家们开始探讨利用大功率高频电波改变电离层的可能性.20世纪6、70年代以后，美国、苏联和一些欧洲国家相继建立了电离层加热实验装置（Thide，1997），并陆续开展了大量电离层人工改变（加热）实验，得到了很多有意义的结果.另外，电离层作为天然的等离子体实验室，具有大尺度，多形态，无边界等条件，是等离子体研究的优良场所，大功率高频电波加热电离层则提供了最佳的研究手段.电离层加热能引起电子温度和电子密度的扰动，造成信息链路的中断或者畸变；也会产生等离子体不均匀体，可对通信和无线电造成干扰.因此，大功率高频电波加热电离层不仅具有科学研究价值，也具有诱人的应用前景.

在电离层电波加热的理论研究方面，国内外学者做了大量的研究.Gurevich（1978）基于非磁化各向同性等离子体假设提出了电离层电波加热的基本理论；Bernhardt用流体力学方程组描述了电离层F区的欠密加热（Bernhardt and Duncan，1982），着重考虑了电波在加热过程中的自聚焦效应；Meltz等建立了适用于低电离层加热的理论模型，并数值模拟了电离层D区、E区的加热实验（Holway and Meltz，1973；Meltz et al.，1982）.黄文耿等（2003，2004）通过考虑电波与低电离层相互作用过程中的自吸收，构建了自洽的物理模型，并计算了电子温度和电子密度的变化；吴军等（2007）研究了北极地区低电离层欧姆加热效应，并进行了数值模拟；汪枫等（2009）在理论上探讨了利用高频泵波激发电离层极低频（ELF）和甚低频（VLF）辐射的可能性；李清亮等（2008）研究了中低纬调制高频加热电离层ELF／VLF辐射，并计算了加热产生的ELF／VLF Hall电流的大小；何昉和赵正予等（2009）提出了一种计算电离层吸收损耗的方法，并利用射线追踪模型定量计算了穿过电离层区域的高

频雷达电波的吸收损耗；汪四成等（2012）计算了HF波对低电离层的变态.

本文在上述理论的基础上，利用电子能量方程、连续性方程计算了电波连续加热条件下电离层电子温度和电子密度的变化，分析了电波能量吸收的主要影响因素，对白天和夜间的加热效果进行了对比，同时给出了不同泵波频率和不同功率加热时电子温度和电子密度的变化结果，以期对不同加热条件下的低电离层加热效果进行预测和评估，为加热实验提供一定的理论指导.

2 基本理论

2.1 低电离层加热原理

在电离层的D区和E区的较低高度上，碰撞过程比较显著，等离子体的输运过程可以被忽略.一般地，在低电离层的高度上，电波的吸收是欧姆吸收，即碰撞吸收.当入射泵波通过低电离层时，损失的能量主要被电子吸收，离子的加热可以忽略.

电子在外加电场中被库仑力加速而获得能量，导致其动力学温度升高，电子又通过与其他粒子的碰撞损失能量，导致其温度下降.显然，电子的加速和碰撞是两个逆过程，即加热过程和冷却过程.在入射泵波为连续波的情况下，一定时间内，电子吸收电波的能量与通过碰撞损失的能量相等，达到能量平衡，于是电子温度趋于一个稳定的值.同时，电子温度的变化会引起电子复合系数的变化，导致电子密度的扰动.

2.2 电子能量方程

其中k、ne和Te分别为Boltzmann常数、电子浓度和电子动力学温度；Q（Te，h）和L（Te，h）分别为电子能量的吸收项和损失项.

2.2.1 电波能量吸收项的计算

单位体积单位时间内吸收的能量随高度的关系为

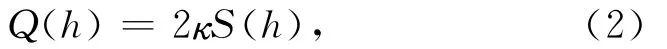
其中S（h）为高度h处的入射电波能流，其随高度的表达式为

式中，ERP为电波的有效辐射功率；h0为电离层的下边界；κ（h′）为电波吸收指数，与（2）式中的κ一致，其表达式为

其中，ω＝2πf，f为高频电波的频率，c为光速，为复折射指数n的虚部，由A－H（Appleton－Hartree）公式计算得到.利用A－H公式计算 时，电子碰撞频率v由下面经验公式确定（Pashin et al.，1995）：式中，方括号中的量代表相应中性成分的密度，Te为电子温度；地磁场采用中心偶极场模式（黄文耿和古士芬，2003）：

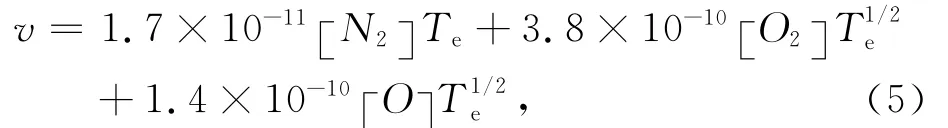
其中，常数B0＝3.085×10－5T，Re为地球的平均半径，λ是磁纬，h为距地面高度.

2.2.2 电波能量损失项的计算

电离层中电子能量的损失机制十分复杂，主要通过碰撞过程完成，常见的损失机制有（Stubbe and Varnum，1972）：①电子与正离子的弹性碰撞；②电子和中性离子的弹性碰撞；③分子O2和N2旋转能级的激发；④分子O2和N2振动能级的激发；⑤原子O电子能级和精细结构的激发.电子能量的损失是上述5项损失的总和.

2.3 连续性方程

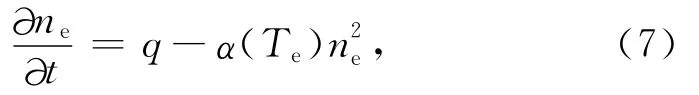
其中，q是产生率，α（Te）是复合系数.对于低电离层，离子主要为分子离子，取电子密度损失过程为平方律模型是合理的，主要考虑NO＋和O＋2的分解复合，则其复合系数可表示为（Gurevich，1978）：

式中，方括号中的量代表相应离子的密度.

3 数值模拟

3.1 边界与初始条件

在本文的计算中，背景电离层参数由IRI2007（国际参考电离层2007）模式计算得出，并且正离子仅保留NO＋和O＋2，参数分布如图1a所示；中性大气背景参数由NRLMSISE－00模式计算得出，参数分布如图1b所示（电离层参数和中性大气参数均为南京地区上空数值）.加热开始前，假设电子温度（Te）、离子温度（Ti）和中性粒子温度（Tn）相等（Te＝Ti＝Tn）.加热地点选在南京地区（32°N，118.5°E），时间为2007年1月1日12LT.低电离层高度取为65～120km，忽略65km以下的电波吸收.层间距取为1km，时间步长取为1μs.

3.2 数值计算流程

在数值计算过程中由电子温度的变化，依据复合系数是温度的函数来计算电子密度的变化，再将这些量作为新的电离层背景，重复以上计算.计算流程如图2所示.

3.3 计算结果

3.3.1 复折射指数虚部和初始吸收能流

地面发射机的参数选取为ERP＝200MW，f＝7MHz，φ＝15°（φ为波法向与地球磁场之间的夹角）.在未加热条件下，由A－H公式计算复折射指数虚部和初始吸收能流，结果分别如图3所示.

可以看出，O波模、X波模分别加热时，折射指数虚部变化的趋势一致.X波模加热时折射指数虚部较O波模加热时大，说明X波比O波易于吸收.O波加热时，在65～120km高度之间折射指数虚部存在两个峰值，分别在72km、97km取得，且后者大于前者；吸收能流也存在两个峰值，分别在70km、97km取得，在100km以上高度吸收能流很少，说明D区是电波的主要吸收区，可造成电波的有效衰减.吸收能流与折射指数虚部在分布趋势上有很好的对应关系，这是因为复折射指数虚部描述的是粒子对电磁波的吸收性质，复折射指数虚部越大，则吸收的能流越多.

图1 初始电离层参数剖面（a）及初始热层大气参数剖面（b）Fig.1 The initial profile of ionospheric parameters（a）and the initial profile of neutral atmospheric parameters（b）

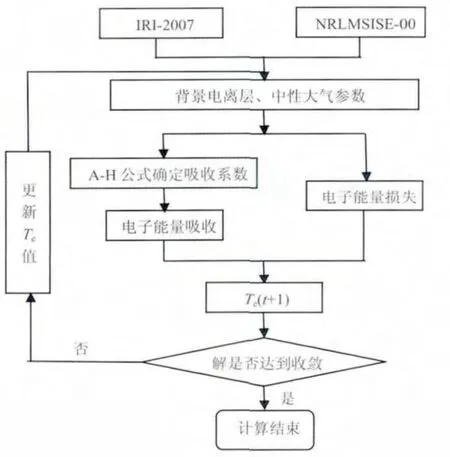
图2 低电离层加热模型计算流程Fig.2 Compute process of lower ionosphere heated model

为了进一步分析图3b中初始吸收能流分布特性，得到了电子密度与碰撞频率比较的剖面图和电子密度与碰撞频率的乘积剖面图，如图4所示.

由图3b可得知在70km和97km，对应于O波和X波的吸收能流出现了极大值，这是由电子密度和碰撞频率两个因素共同决定的.在碰撞频率一定时，电子密度越大，吸收个体越多，则吸收能流越大；在电子密度一定时，随着碰撞频率的增加，等离子体带电粒子损失增加，则其对高频电波的吸收能流也增加.电子密度、碰撞频率二者的乘积与吸收能流呈正相关.综合图3b、图4b可看出，电子密度、碰撞频率二者的乘积与吸收能流的分布趋势非常相似，也存在两个极值，分别在72km和97km取得.结合图4a，在72km处，碰撞的因素占优；而在97km处，电子密度的因素占优.

图3 折射指数虚部剖面（a）及初始吸收能流剖面（b）Fig.3 Refractive index profile of the imaginary part（a）and energy flow profile of initial absorbed（b）

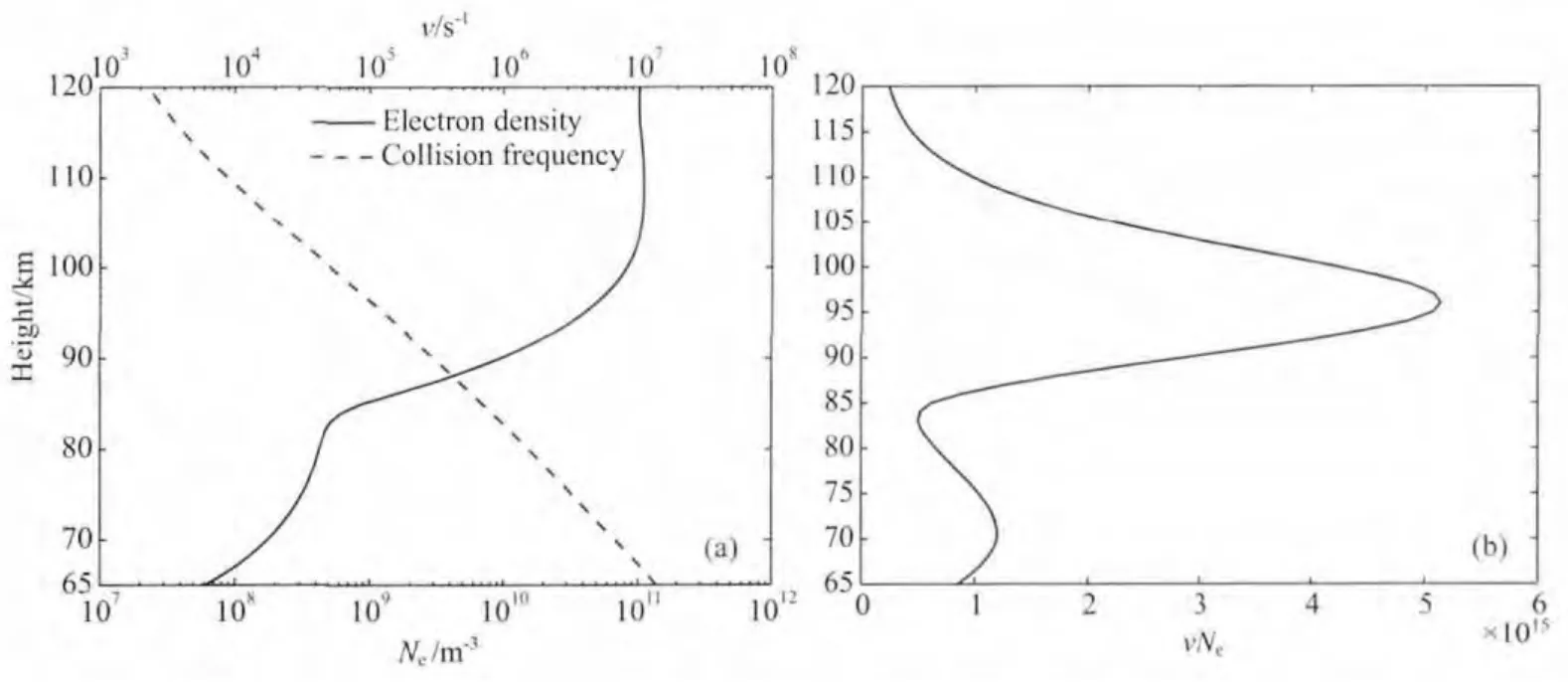
图4 电子密度与碰撞频率的剖面（a）及乘积剖面（b）Fig.4 The profile of electron density and collision frequency（a）and product profile of the electron density and collision frequency（b）

3.3.2 电子温度扰动量和电子密度增量（O波模）

（1）白天加热效果（LT＝12）

图5a是加热不同时刻的电子温度剖面，可看出10μs后65km处的电子温度增加了近90K；到160μs时电子温度增幅开始出现极值，在67km处取得，且电子温度增幅极值高度以下的电子温度已达到饱和；到640μs时电子温度的增幅已很小，75km以下的电子温度已达到饱和；在前640μs的时间内，65～85km之间的电子温度明显增加；640μs以后，电子温度的明显增加主要在75～100km之间；到6000μs时，电子温度基本不再变化；从图5a中还可以看出随着电离层高度的增加，电子温度达到饱和的时间也变长.从图5b中可看出65～85km之间的电子密度基本没有变化，这是因为65～85km之间的背景电子密度很小，在电子温度增加复合系数减小后（可由图6得知）也不能引起电子密度的明显变化；随着时间的推移，相同加热时间内电子密度增幅越来越小，到24000μs时电子密度已基本稳定，电子密度最大增幅高度为96km.在6000μs时，电子密度增幅已达15000cm－3.通过对比可以发现，电子温度的弛豫时间为μs量级，电子密度的弛豫时间为ms量级.

（2）夜间加热效果（LT＝24）

由图7可以看出，夜间电子温度的变化与白天相比，变化趋势上基本一致，但加热效果明显好于白天，电子温度的增幅十分明显，最高增加到近2400K，由图8可以看出，夜间电子温度加热后最多可增加12倍，而白天最多只可增加3倍.这主要是因为夜间电子密度比白天小两个量级以上，已经成为能流损失的主要影响因子，故夜间能流损失比白天小，使得能流净吸收与电子密度的比值在夜间大于白天.从计算结果中还可知夜间的电子温度弛豫时间与白天的数值基本一致.

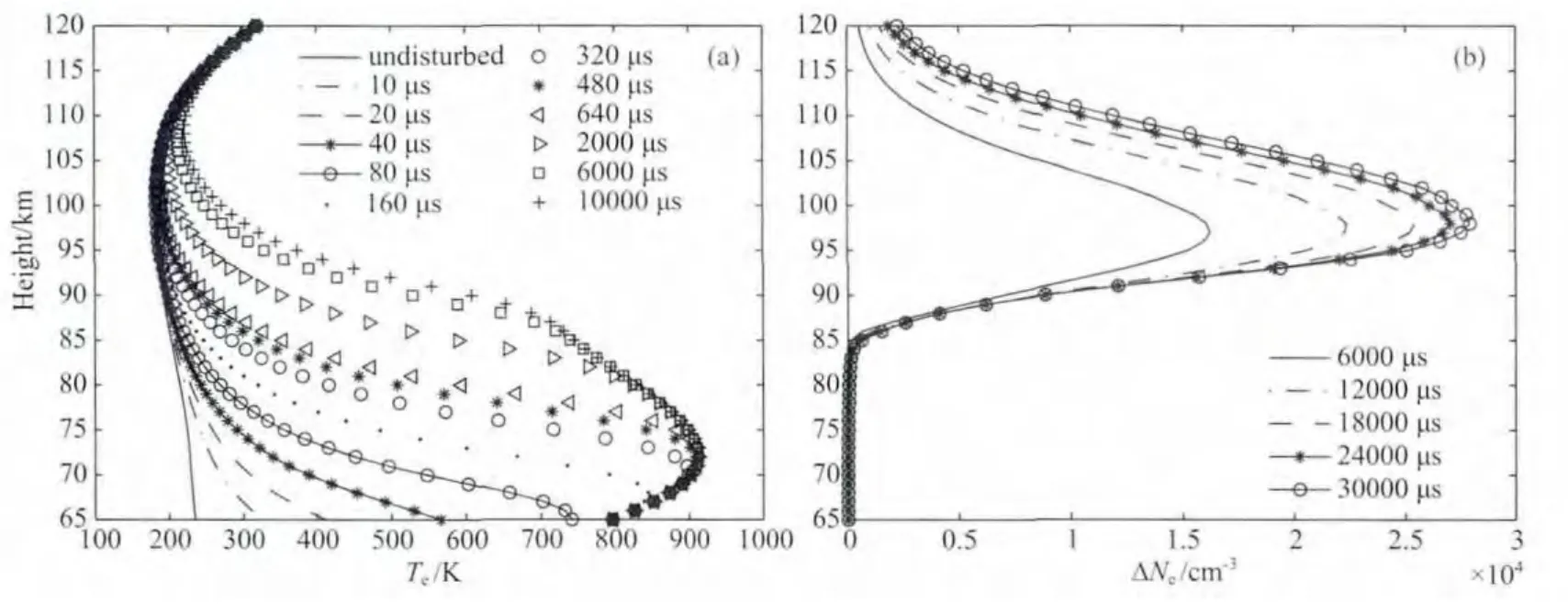
图5 加热不同时刻的电子温度剖面（a）及电子密度增量剖面（b）Fig.5 Electron temperature profile at different times（a）and electron density increment profile at different times（b）

图6 复合系数随温度变化Fig.6 Recombination coefficient varies with temperature

图7 加热不同时刻的电子温度剖面Fig.7 Electron temperature profile at different times

由图9可知，夜间电子密度增幅较小，在同一时间间隔内，电子密度增量基本一致，最大增量高度逐渐变大.由图10可知，在欠密加热条件下，夜间电子密度增长率要小于白天.复合系数由电子温度与电子密度共同影响，夜间最高电子温度是白天的2倍多，而且夜间电子密度比白天小2个量级以上，故夜间的复合系数要小于白天，结合连续性方程，可知夜间电子密度增长率要小于白天.从计算结果中还可知夜间的电子密度弛豫时间比白天的数值大.

图8 温度增量与初始温度比值Fig.8 The ratio of temperature increment with the initial temperature

图9 加热不同时刻的电子密度增量剖面Fig.9 Electron density increment profile at different times

3.3.3 不同频率泵波加热时电子温度与电子密度的变化（O波模）

从图11a中可以看出，电子温度增幅随泵波频率的增加而减小，这可以理解为外场频率越高，电子吸收外场能量的周期越短，则吸收的能量就越少；电子温度最大增幅高度也随频率的增加而减小.当泵波频率为6MHz时最大增幅可达847K.从图11b中可以看出，电子密度增幅随频率的增加而减小，这是因为泵波频率高时，电子温度增幅小，则复合系数较大，电子密度扰动幅度就会变小；电子密度最大增幅高度随频率增加略有增加.当泵波频率为6MHz时最大增幅可达54000cm－3.

3.3.4 不同功率泵波加热时电子温度与电子密度的变化（O波模）

图10 密度增量与初始密度比值Fig.10 The ratio of density increment with the initial density

图11 不同频率泵波加热稳态时电子温度剖面 （a）及加热稳态时电子密度增量剖面 （b）Fig.11 Steady－state electron temperature profile heated by different frequency pump wave（a）and steady－state electron density increment profile heated by different frequency pump wave（b）

图12 不同功率加热稳态时电子温度剖面（a）及电子密度增量剖面（b）Fig.12 Steady－state electron temperature profile heated by different power（a）and steady－state electron density increment profile heated by different power（b）

从图12a中可以看出，电子温度增幅随有效入射功率的增加而增加，这可以理解为有效入射功率越高，单位时间内入射的能量就越多，电子单位时间内吸收的能量就越多，温度增幅越大；电子温度最大增幅高度也随有效入射功率的增加而增加.当有效入射功率为5MW时最大增幅可达1500K.从图12b中可以看出，电子密度增幅随有效入射功率的增加而增加，这是因为有效入射功率高时，电子温度增幅大，则复合系数较小，电子密度扰动幅度就会变大；电子密度最大增幅高度随有效入射功率增加略有增加.当有效入射功率为5MW时最大增幅可达140000cm－3.

4 结论和讨论

在电离层水平均匀的假设下，忽略反常吸收及热传导和扩散过程，基于电子能量方程和连续性方程数值计算了高频泵波加热低电离层时电子温度和电子密度的增幅.得到了如下结果：

（1）电波垂直射入电离层后，与等离子体相互作用，通过碰撞吸收使不同高度的电子温度和密度均有一定程度的升高.加热一段时间后，电子温度和电子密度会达到饱和状态，电子温度达到饱和所需的时间远小于电子密度的饱和时间，前者具有微秒量级，后者是毫秒量级；

（2）在同一入射频率和功率下，电子密度和碰撞频率是影响吸收能流的重要因素，在低电离层X波比O波更容易吸收；

（3）在功率相同，入射频率在临界频率的加热条件下，夜晚的电子温度变化率明显大于白天的，但夜晚的电子密度变化率小于白天的；夜间电子温度弛豫时间与白天的数值基本一致，而夜间电子密度弛豫时间比白天的数值大；

（4）在相同条件下，入射电波频率越高，电子温度和电子密度的扰动幅度越小，饱和时间也越短；有效入射功率越高，电子温度和密度的扰动幅度越大，饱和时间也越长.

本文的加热理论模型可用于对相关试验结果进行预测和试验参数的选择提供参考，根据本文结论，为获得更加有效的加热效果，可增大加热系统的有效辐射功率、或根据实时背景选择合适的加热频率.同时本文所用的模型仅适用于“欠密”加热，即入射泵波频率大于等离子体频率（f＞fN），对于“过密”加热（f＜fN）情况，由于在电波的发射点附近，入射波与反射波相互叠加形成“驻波”，电场可能很大，反常吸收作用明显；电离层的吸收和电子能量的损失与背景电离层和中性大气条件有关，而电离层参数和中性气体参数存在明显的地区差异，本文利用经验模式得出的南京地区上空的电离层参数和中性气体参数进行了数值模拟，且经验模式IRI2007和NRLMSISE00所得数据与实际大气状况存在一定差距.上述情况虽对定性结论无影响，但都会影响到定量计算的精度，还需进一步研究.

Bernhardt P A，Duncan L M.1982.The feedback－diffraction theory of ionospheric heating.J.Atmos.Terr.Phy.，44（12）：1061－1074.

Gurevich A V.1978.Nonlinear Phenomena in the ionosphere.Berlin：Springer－Verlag.

He F，Zhao Z Y.2009.Ionospheric loss of high frequency radio wave propagated in theionospheric regions.Chinese.J.Radio Sci.（in Chinese），24（4）：720－723.

Holway L H Jr，Meltz G.1973.Heating of the lower ionosphere by powerful radio waves.J.Geophys.Res.，78（34）：8402－8408.Huang W G，Gu S F.2003.Interaction between the powerful highfrequency radio wave andthe lowerterrestrial ionosphere.Chinese.J.Space Sci.（in Chinese），23（3）：181－188.

Huang W G，Gu S F，Gong J C.2004.Ionospheric heating by powerful high－frequencyradioWaves.Chinese.J.Radio Sci.（in Chinese），19（3）：296－301.

Li Q L，Yang J T，Yan Y B，et al.2008.ELF／VLF waves radiated by modulated HFheatingionospheric in mid－latitude and equatorial regions.Chinese.J.Radio Sci.（in Chinese），23（5）：883－887.

Meltz G，Rush C M，Violette E J.1982.Simulation ofD and E region high－powermicrowave heating with HF ionospheric modification experiments.Radio Science，17（3）：701－715.

Pashin A B，Belova E G，Lyatsky W B.1995.Magnetic pulsation generation by apowerful ground－based modulated HF radio transmitter.J.Atmos.Terr.Phy.，57（3）：245－252.

Stubbe P，Varnum W S.1972.Electron energy transfer rates in the ionosphere.Planetary and Space Science，20（8）：1121－1126.Thide B.1997.Artificial modification of the ionosphere：preface.J.Atoms.Solar.－Terr.Phys.，59（18）：2251－2252.

Wang F，Zhao Z Y，Zhang Y N.2009.Numerical modeling of ionospheric current artificialmodulation at low latitude.Chinese J.Geophys.（in Chinese），52（4）：887－894.

Wang S C，Fang H X，Yang S G，et al.2012.Heating of lower ionosphere by powerfulhigh frequency radio wave.Chinese.J.Space Sci.（in Chinese），32（6）：818－823.

Wu J，Che H Q，Wu J，et al.2007.A simulation of the heating effect of high power radiowave on the lower polar ionosphere.Chinese Journal of Polar Research （in Chinese），19（3）：171－180.

附中文参考文献

何昉，赵正予.2009.电离层对高频电波吸收衰减的影响研究.电波科学学报，24（4）：720－723.

黄文耿，古士芬.2003.大功率无线电波与低电离层的相互作用.空间科学学报，23（3）：181－188.

黄文耿，古士芬，龚建村.2004.大功率高频无线电波加热电离层.电波科学学报，19（3）：296－301.

李清亮，杨巨涛，闫玉波等.2008.中低纬调制高频加热电离层ELF／VLF辐射模拟.电波科学学报，23（5）：883－887.

汪枫，赵正予，张援农.2009.低纬地区电离层电流的人工调制数值模拟.地球物理学报，52（4）：887－894.

汪四成，方涵先，杨升高等.2012.大功率无线电波加热低电离层.空间科学学报，32（6）：818－823.

吴军，车海琴，吴健等.2007.北极区低电离层加热效应的数值模拟研究.极地研究，19（3）：171－180.