卵形弹体侵彻混凝土开坑区侵彻阻力计算*
柴传国,皮爱国,武海军,黄风雷
(北京理工大学爆炸科学与技术国家重点实验室,北京100081)
弹体在着靶时通常存在一定倾角,弹头在非轴对称力作用下使得弹体从开坑区就发生偏转,弹体偏转结束时的弹体姿态和速度对后续侵深计算会产生重要影响。目前应用较广的Forrestal公式只给出了弹头在开坑区的阻力,并未给出弹头表面的应力形式[1-4],因此难以计算弹头表面应力对弹体产生的偏转力矩,给准确计算弹体偏转结束时的弹体姿态和速度等参量带来困难,并影响了开坑区弹体偏转角度和开坑区结束时弹体速度的计算精度[5-7]。为了研究弹体的姿态偏转角度,需要对弹头表面在开坑区的侵彻阻力的清晰描述。本文中基于此开展弹头曲径比为2和4.55的卵形弹体在400、600和800m/s速度下的混凝土侵彻实验。采用最小二乘法对实验数据进行分析,基于分析结果计算了开坑区的侵深和速度,并与同等条件下采用Forrestal公式的计算结果进行了对比,得到相应的公式的适用范围。
1 Forrestal公式
在混凝土侵彻阻力计算中应用最广的是Forrestal公式,其将弹体侵彻半无限混凝土靶的过程可分为开坑区和隧道区2个阶段。M.J.Forrestal等[2]认为开坑区的侵彻阻力随开坑深度线性增加,并认为开坑深度是弹体直径d的2倍,开坑区(0<z≤2d)和隧道区(z>2d)阻力形式为:
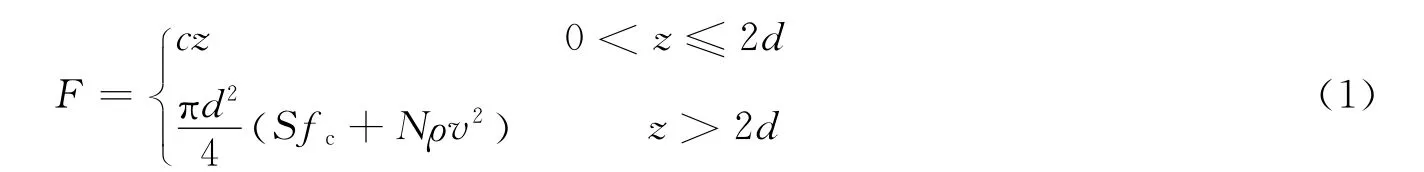
式中:z是弹轴方向的侵彻深度,F是弹体的侵彻阻力,c是开坑区的侵彻阻力系数,v1是开坑区结束时的弹体速度,vs是弹体初始撞击速度,v是弹体侵彻的瞬时速度,a是弹身半径,S是靶体静态阻力系数,fc是靶体的无侧限抗压强度,m是弹体质量,N是弹头系数,ρ是靶体密度,ψ是弹头的曲径比。
M.J.Forrestal等[2]通过边界条件和初始条件求解开坑区侵彻阻力方程得到开坑区的侵彻阻力系数c和开坑区结束时的弹体速度v1:
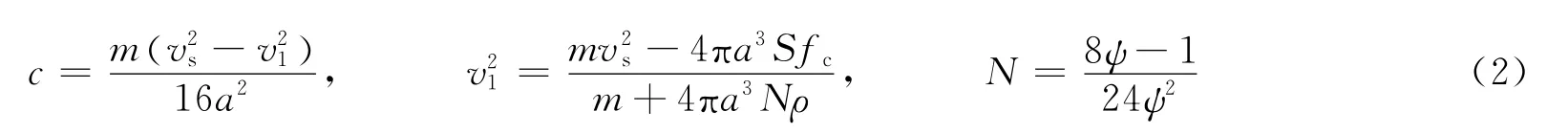
由上述事实可知,M.J.Forrestal等[2]提出的开坑区侵彻阻力满足线性关系的假设,不是基于混凝土侵彻实验数据,而是将基于土壤侵彻的加速度曲线提出的开坑区的侵彻阻力与侵彻深度满足线性关系的假设,未作任何修正地直接应用于混凝土侵彻。开坑区阻力系数c是在上述假设下,基于混凝土侵彻实验数据,由隧道区和开坑区的交界处阻力相等的边界条件得到。因此,描述混凝土侵彻问题的Forrestal公式的参数都是基于实验数据,能较好地计算混凝土的侵彻深度。
但上述求解过程中人为定义开坑区深度为2d,和开坑区阻力形式为线性关系,并不能反应真实的物理过程,也不能给出开坑区的侵彻阻力的应力表达式。Chen Xiao-wei等[5]在计算开坑区弹体姿态偏转时采用Forrestal公式给出的开坑区总侵彻阻力的分力进行弹体偏转的计算,这一方法由于Forrestal公式阻力形式的限制而无法准确计算弹体在非轴对称情况下的弹体阻力和偏转力矩,因而对弹体姿态偏转的预估带来困难。
2 实验研究
实验使用2种卵形弹体,弹头的曲径比分别为2和4.55(文中称为OP2型弹和OP5型弹)。弹身直径d均为40mm,弹身长度L均为160mm,弹体材料为30CrMnSiNi2A高强度合金钢,通过改变弹体内部开孔深度和开孔直径确保弹体质量均为1.4kg以及弹体质心处于弹体中部,图1给出了2种弹体的结构示意图。

图1 2种型号弹体结构示意图Fig.1 Schematic of two kind of ogive-nose projectiles
实验用混凝土圆柱靶体直径是1.2m,高度是1.2m,侧面采用3mm厚钢板围箍。混凝土的标准立方体块压缩强度是18.5MPa,密度是2 238kg/m3。实验采用北京理工大学爆炸科学与技术国家重点实验室炮管内径152mm的一级气体炮作为加载装置。采用高速摄影仪记录弹体的着靶速度和着靶姿态。图2所示是OP2型弹在初始撞击速度为431m/s时的开坑区照片。

图2 侵彻过程中开坑区照片Fig.2 Pictures of crater region during penetration process
OP2型弹和OP5型弹在不同撞击速度时,开坑区的弹体速度和侵深数据如表1所示。
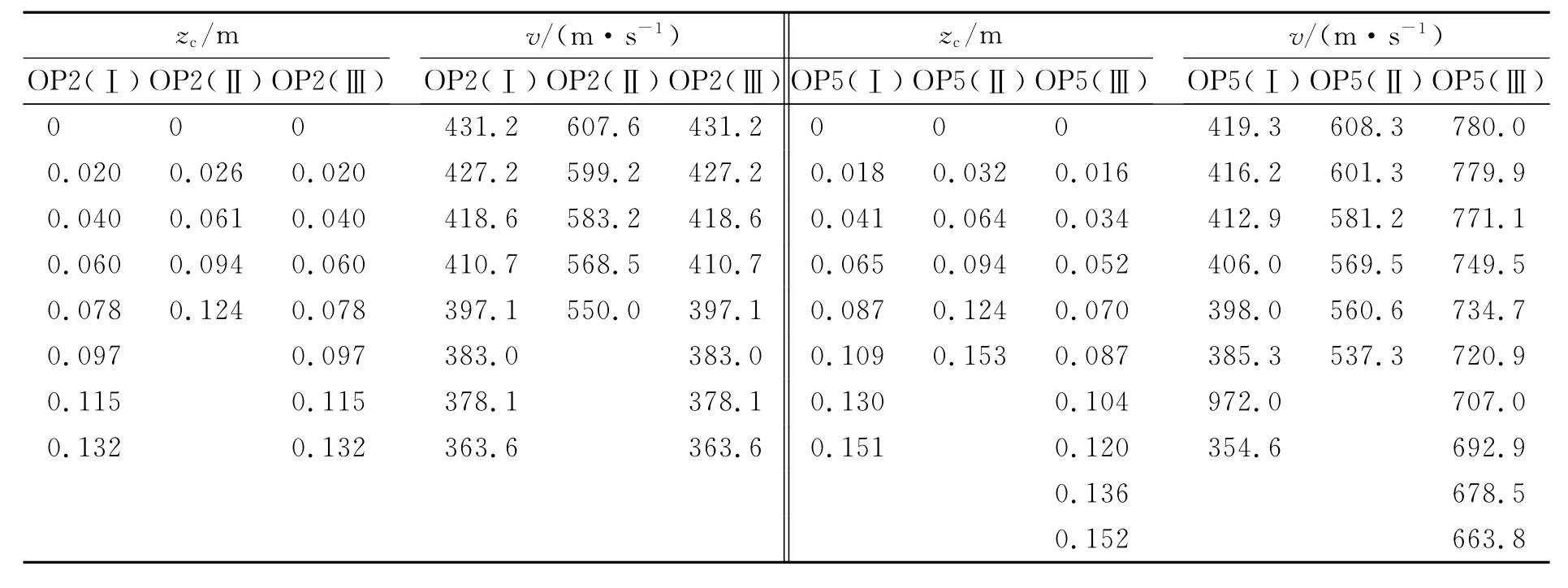
表1 开坑区在侵彻过程中的数据Table 1 Experimental data of crater region during penetration process
3 最小二乘法分析
为了探讨开坑区弹头的应力表达式,对开坑区的侵彻实验数据采用最小二乘法进行拟合,分析开坑区的侵彻阻力形式,并对拟合结果进行检验。在拟合分析开坑区阻力形式时,采用开坑区总的动能消耗ΔE进行拟合,而在检验开坑区阻力的拟合分析结果时,采用开坑区不同侵深时的速度进行拟合。由于在拟合分析开坑区阻力形式时仅使用了初态和终态2个速度点,而检验拟合得到的阻力形式时则采用了侵彻过程的多个速度点,保证了检验过程的有效性。
参考M.J.Forrestal等[2]对侵彻阻力的描述,认为开坑区的侵彻阻力与靶体密度ρ、靶体无侧限抗压强度fc、弹体直径d、弹头系数N和侵彻速度v有关,设开坑过程中弹头表面应力形式为:

当开坑区侵深zi时,弹头的轴向阻力可表示为:
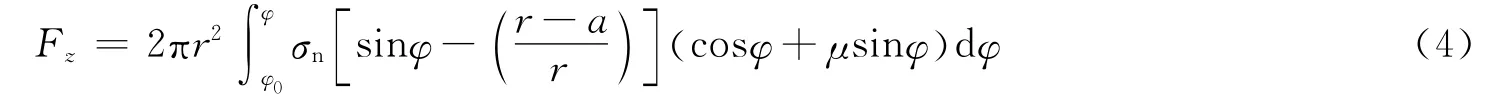
式中:A和B均为待定系数,r是弹头的曲率半径,a是弹身半径,μ是摩擦系数,φ0是弹头侵彻的初始角度,φ是侵深为zi时的角度,如图3所示。

图3 弹头参量示意图Fig.3 Penetration parameters of ogive-nose projectile
将开坑区侵深分成一系列小的位移δz,每个小位移内弹体速度和弹靶接触面积均恒定,则通过式(4)可求得侵深zi时的开坑区阻力F(zi)。由侵深zi时的开坑区侵彻阻力F(zi)和小位移δz可求得在每一个小位移δz内的弹体动能变化δEi,进而求得小位移δz结束时的侵彻速度vi和下个小位移δz初始时刻的侵彻阻力F(zi+1)。不断重复上述过程,得到开坑区每个侵深时的速度和位移关系。具体过程可分别计算:,然后代入式(3)~(4)。当计算侵彻深度zi与开坑侵深zc相等时,停止计算,输出用待定系数A和B表示的弹体开坑侵深zc时的侵彻速度和动能消耗ΔEi,摩擦系数取0.01。
采用系数A和B来表示的弹体开坑侵深zc时消耗的动能ΔEi,基于最小二乘法对实验测得的开坑过程中的消耗的动能ΔE进行拟合,得到相同侵深时计算得到的消耗的弹体动能ΔEi与实验值偏差的平方和最小时的系数A和B,开坑侵深zc、撞击速度vs、开坑侵深对应的侵彻速度vc和弹体动能消耗ΔEi,如表2所示。

表2 最小二乘法拟合用的数据Table 2 Parameters for least square fitting
取表1中最大侵深为最小二乘法拟合使用的开坑侵深zc,取OP2型弹体的开坑侵深zc为3个速度下的平均值0.128m,OP5型弹体的开坑侵深zc为3个速度下的平均值0.152m。其中,对OP2型弹的数据拟合得到A=1.715×10-7,B=1.486×10-1,对OP5型弹 的 数 据 拟 合 得 到 A = 3.67×10-7,B =1.671×10-1,拟合结果如图4所示。
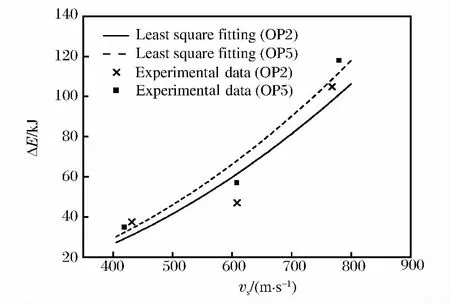
图4 最小二乘法对弹体开坑过程中耗能的拟合分析Fig.4 Fitted curves of kinetic energy decrease during cratering
将拟合得到的A和B的值代入式(3)后比较阻力的静态部分和惯性部分的大小,可知开坑过程中侵彻阻力中的静态部分比惯性部分小8个数量级,可忽略忽略侵彻过程中阻力中的静态部分的影响,只考虑阻力中的惯性部分,可将开坑过程中侵彻阻力的弹头表面应力形式表示为:

将式(5)在弹头区域进行面积分得到开坑过程中所受到的阻力,并与Forrestal公式对开坑区侵彻阻力描述进行比较,求解了不同开坑侵深时的侵彻速度,并与高速摄影仪记录到的不同撞击速度下弹体侵彻速度进行了比较,如图5~6所示。需要说明的是,Forrestal公式中的开坑侵深为2倍弹体直径,而OP2型和OP5型弹在3个撞击速度下的实际开坑侵深分别是0.09、0.11和0.13m以及0.12、0.15和0.11m,均大于2倍的弹体直径。由于Forrestal公式中的侵彻阻力系数c的计算需要vs和v1这2个速度点,但通过实验难以测得准确的v1,因此使用实验中得到的vc近似代替,vc为对应侵彻深度zc时的速度,进而得到Forrestal公式的计算结果。
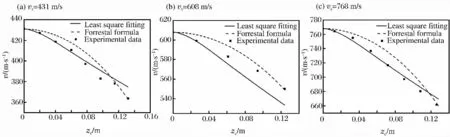
图5 OP2型弹开坑区侵彻速度和侵深的关系Fig.5 Relation between penetration velocity and penetration depth during cratering
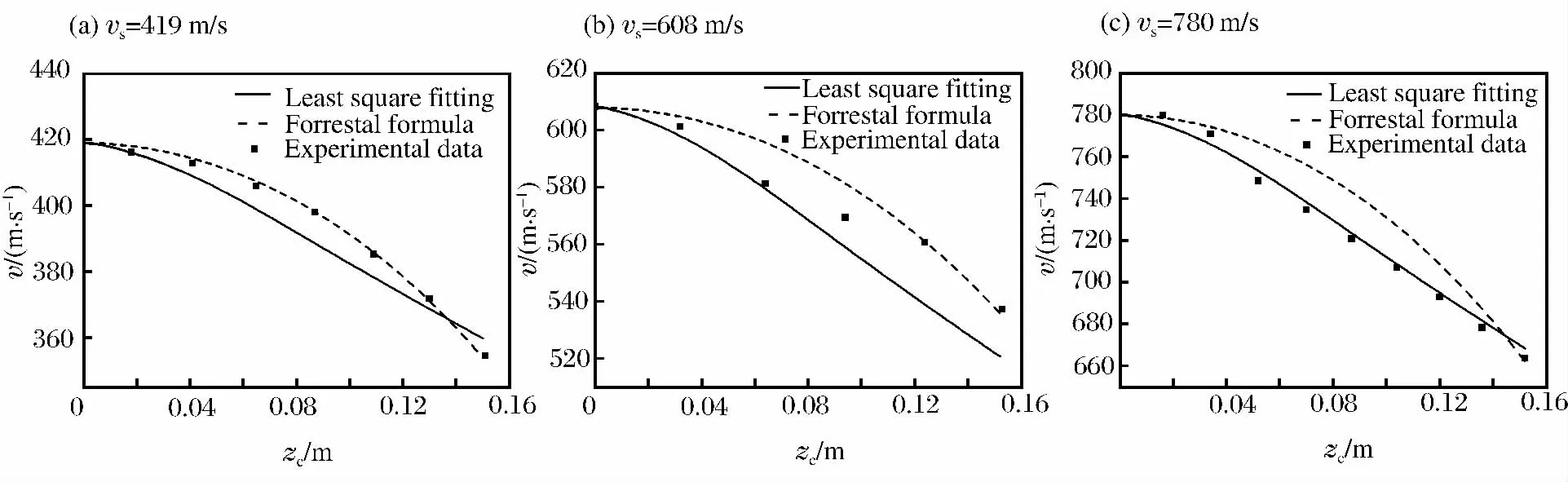
图6 OP5型弹开坑区速度和侵深的关系Fig.6 Relation between penetration velocity and penetration depth during cratering
由图5(a)和6(a)中可以看出,撞击速度在400m/s速度区域时,Forrestal公式能更好地描述弹体的速度变化。由于Forrestal公式认为开坑过程中阻力主要由静态部分组成,因此可以认为在撞击速度较低时,阻力中的静态部分起主要作用。由图5(c)和6(c)可以看出,撞击速度在800m/s速度区域时,式(5)能较好地描述弹体的速度变化。式(5)表明开坑过程中阻力主要由惯性部分组成,因此可以认为,当弹体的撞击速度进入800m/s区域时,阻力中的惯性部分起主要作用。由图5(b)和6(b)可以看出,撞击速度在600m/s速度区域时,实验点散落在Forrestal公式和式(5)之间,此时,阻力中的静态部分和惯性部分共同起作用。
由表2可知,OP2型弹在初始撞击速度分别为431、608和768m/s时,开坑区消耗的动能分别占弹体初始动能的28.90%、18.17%和25.81%。OP5型弹在初始撞击速度分别为419、608和780m/s时,开坑区消耗的动能分别为弹体初始动能的28.39%、21.90%和27.58%。开坑区弹体消耗的动能占弹体初始动能的比例较大,因此,研究弹体在开坑区的侵彻阻力的准确表达式对计算弹体剩余侵彻能力和弹体在开坑区的姿态偏转很有意义。
4 结 论
(1)Forrestal公式能较好地描述卵形弹体速度在接近400m/s时,开坑区的侵彻阻力和速度变化,拟合得到的式(5)能较好地描述卵形弹体速度在接近800m/s时,开坑区的侵彻阻力和速度变化。
(2)弹体速度在接近400m/s时,开坑过程中的侵彻阻力以静态部分为主。随着撞击速度的增加,侵彻阻力中的惯性部分越来越大。当弹体撞击速度接近800m/s时,开坑过程中的侵彻阻力以惯性部分为主,此时,可以忽略阻力中的静态部分。当撞击速度介于二者之间的速度区域时,静态部分和惯性部分对侵彻阻力共同起作用。
[1]Warren T L,Hanchak S J,Poormon K L.Penetration of limestone targets by ogive-nosed VAR 4340steel penetrators at oblique angles:Experiments and simulations[J].International Journal of Impact Engineering,2004,30(10):1307-1331.
[2]Forrestal M J,Altman B S,Cargile J D,et al.An empirical equation for penetration depth of ogive-nose penetrator into concrete targets[J].International Journal of Impact Engineering,1994,15(4):395-405.
[3]Forrestal M J,Frew D J,Hanchak S J,et al.Penetration of grout and concrete targets with ogive-nose steel penetrators[J].International Journal of Impact Engineering,1996,18(5):465-476.
[4]Frew D J,Forrestal M J,Hanchak S J.Penetration experiments with limestone targets and ogive-nose steel penetrators[J].ASME Journal of Applied Mecheanics,2000,67(4):841-845.
[5]Chen Xiao-wei,Fan Shou-chang,Li Qing-ming.Oblique and normal perforation of concrete targets by a rigid penetrator[J].International Journal of Impact Engineering,2004,30(6):617-637.
[6]马爱娥,黄风雷.弹体斜侵彻钢筋混凝土的试验研究[J].北京理工大学学报,2007,27(6):482-486.Ma Ai-e,Huang Feng-lei.Experimental research on oblique penetration into reinforced concrete[J].Transactions of Beijing Institute of Technology,2007,27(6):482-486.
[7]吕中杰,徐钰巍,黄风雷.弹体斜侵彻混凝土过程中的方向偏转[J].兵工学报,2009,30(增刊2):301-304.LüZhong-Jie,Xu Yu-wei,Huang Feng-lei.Transverse deflection of projectile obliquely penetrating into concrete[J].Acta Armamentarii,2009,30(Suppl 2):301-304.

