基于LS-DYNA的高速破片水中运动特性流固耦合数值模拟*
康 德,严 平
(海军工程大学兵器工程系,湖北 武汉430033)
水下爆炸对目标的破坏除了冲击波作用,高速破片的作用也不可忽视。爆炸产生的破片初始速度可以达到1 000m/s以上,具有很强的侵彻破坏能力[1]。破片对典型水下目标结构的毁伤效果主要取决于破片在水中的运动特性和侵彻能力。研究高速破片在水中的运动特性对于典型水下目标的抗破片侵彻能力设计具有重要意义。
水下物体的高速运动是一个复杂的多相流运动,涉及到大变形、高应变率。由于理论分析的复杂性和实验研究的高成本,数值模拟以其经济性与高效性日益成为研究的重要手段。
本文中利用ANSYS/LS-DYNA有限元程序对速度在1 000~2 500m/s的立方体破片在水介质中的运动进行了数值模拟,得到了破片的速度衰减曲线,冲击波传播规律。分析了破片墩粗变形规律及其对侵彻阻力的影响,得到了高速破片的侵彻能力随速度的变化规律。其计算结果可为水中目标易损性分析提供有益的参考和依据。
1 数值模型
ALE算法是近场水下爆炸流固耦合以及大变形分析中应用得最为有效的方法,能很好的解决流体-固体耦合问题,可以克服单元严重畸变引起的数值计算困难,并实现流体-固体耦合的动态分析[2]。对破片划分Lagrange型网格,对水域划分ALE型网格,ALE算法先执行一个或几个Lagrange时步计算,此时单元网格随材料流动而产生变形,然后执行ALE时步计算。LS-DYNA可方便地将Euler有限元网格与全Lagrange网格耦合,以处理流体与结构在各种复杂载荷条件下的相互作用问题。
模型由破片、水域组成。常用来研究的破片,形状一般为球形、柱形和方形。数值模拟中选用长方体破片,破片采用Lagrange单元描述,水介质采用欧拉单元描述,单元使用单点欧拉算法,并且利用关键字*CONSTRAINED_LAGRANGE_IN_SOLID将破片与水介质耦合,通过采用ALE算法实现高速破片模型水下运动过程的数值模拟计算。
建立模型时破片采用LS-DYNA提供的一种考虑应变率影响的各向同性弹塑性材料Johnson-Cook模型,其屈服函数数学描述如下:
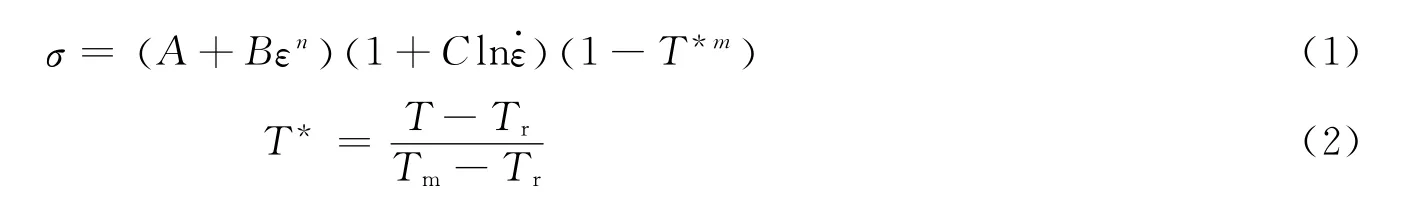
水采用Null材料模型,水的状态方程采用Grüneisen状态方程:
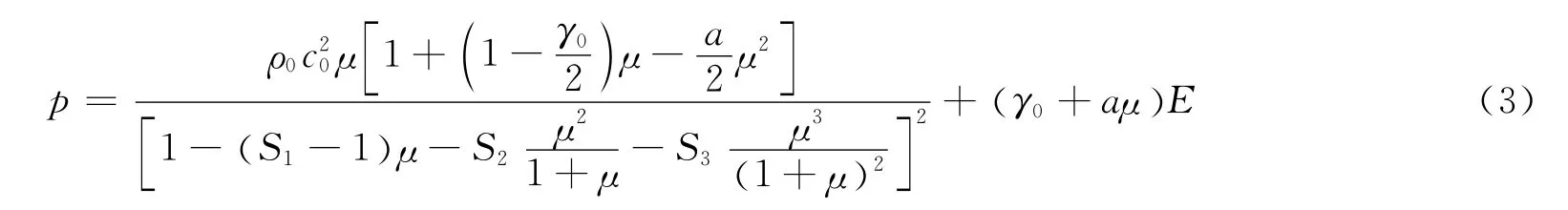
式中:p为压力,E为体积内能,c0为介质中初始声速,取1 480m/s,S1、S2、S3是冲击波输入参数,取S1=1.75,S2=S3=0,通常根据水介质的冲击实验数据确定;ρ0为常温状态下水初始密度,ρ为水当前密度,μ为介质压缩比1;γ0=0.493 4为 Grüneisen初系数,a为 Grüneisen系数修正项。[4]
2 数值模拟结果与分析
2.1 入水破片速度衰减规律
水中破片速度衰减规律的推导可基于刚体力学给出的破片侵彻过程所受的总阻力

式中:CD是阻力系数,ρ是靶材密度,即水的密度,S表示破片最大横截面积,v是破片侵彻速度。令减速系数通过积分可得,其中t为破片水中运动的时间。
为具体研究速度衰减规律,对初速1 200m/s破片在10m水深进行数值模拟,如图1所示,曲线描述了破片速度随时间的变化情况。由图1可看出破片水中运动开始阶段,速度衰减快,破片头部接触区域的水表现出巨大的惯性效应,破片动能很快转化为周围液体的动能。到运动后期,随着速度的降低,破片头部与液体间的速度梯度下降,水的惯性效应减小,破片加速度降低,使破片速度衰减放缓。
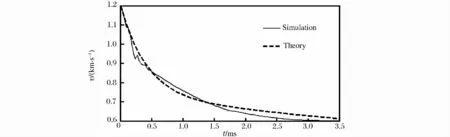
图1 速度衰减曲线Fig.1 Histories of velocity attenuation
实验指出,CD在一定速度范围内可取成常数[5]。如取实验值CD=0.35,则δ0=3.365。图1中虚线表示按v=v0e-δ0x计算的结果。可见在早期,数值计算与经验公式相差不大。但在后期,当侵彻速度较低时,尽管两条曲线趋势接近,量值上相差仍然不小。这与假定CD为常数有关。事实上随着侵彻速度的降低CD应该增大,因为破片侵彻过程中水介质对破片有一定的侵蚀磨损作用,破片迎流面积会变化,破片发生墩粗变形,阻力系数的变化主要由破片的墩粗变形引起的。
2.2 墩粗变形特性
高速破片在水下初始运动时刻,将产生巨大的压力,而使头部发生墩粗变形,其典型变形形态如图2所示。由于头部墩粗,破片水中侵彻时迎水面积增大。在破片初速1 000~2 500m/s的范围内等间隔取16个离散点分别进行计算,得出各自的墩粗率,其中墩粗率-1,A0为初始迎流面积,A为墩粗变形后面积。经拟合得破片头部迎水面积随初速的变化曲线,如图3所示。
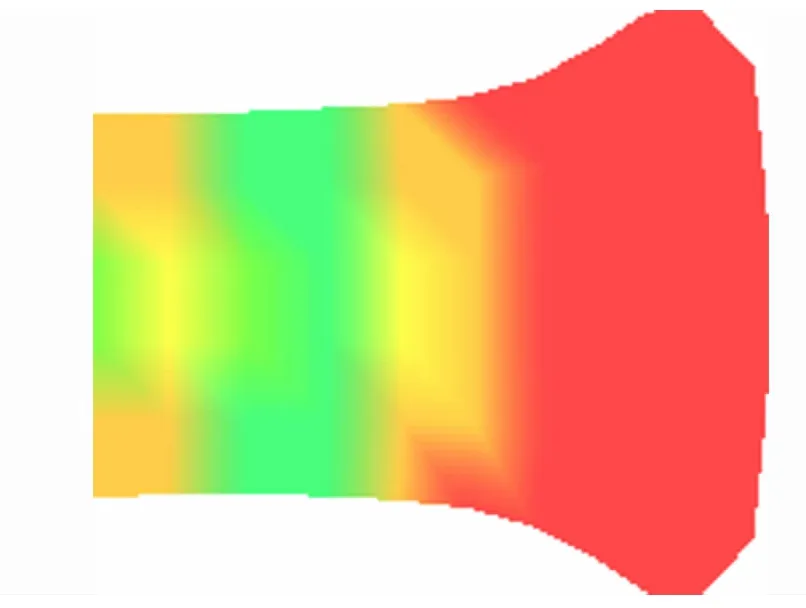
图2 高速破片墩粗变形形态Fig.2 Mushrooming shape of high velocity fragment
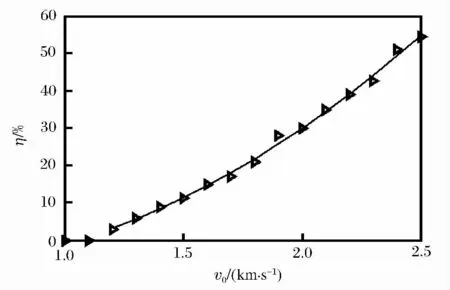
图3 墩粗率与破片初速关系曲线Fig.3 Relation between the mushrooming rate and initial velocity
由图3可知,当破片初始速度小于1000m/s时,破片头部无明显墩粗;当初速大于1 200m/s时,破片头部墩粗显著增加,头部迎流面积近似随初始速度平方的增大而增大。其主要原因是,破片运动初始阶段受到的侵彻阻力主要是水的惯性压力,假设水为Bernoulli方程的不可压缩的无粘性流体,根据Tate-Alekseevskii[6]弹体侵彻模型,则破片受到的压力p可表示为

式中:ρ为靶体即水的密度;v为破片的侵彻速度,近似等于初始破片速度;Rt定义为与靶体材料的剪切强度相关的抗侵彻强度,对于水介质,可取Rt=0。对于高速破片水中侵彻问题,p随初速平方的增大而增大,当p大于破片材料的动态抗压屈服强度σd时,破片开始发生墩粗变形。破片静态屈服强度σs取为207MPa,低碳钢材料σd约为静态屈服强度的2~3倍。因此,当初始大于910~1 115m/s时,低碳钢材料破片开始发生显著的墩粗变形。
2.3 冲击波
破片在水中引起的冲击波效应是早期的重要毁伤因素。初速1 200m/s的破片在入水298.11和508.19μs所形成的冲击波波形态如图4所示。可以看到,当破片的侵彻速度小于水中的音速(约1 500m/s)时,冲击波近似球形向四周传播,并且球形冲击波始终位于破片的前方(脱体球形冲击波)。
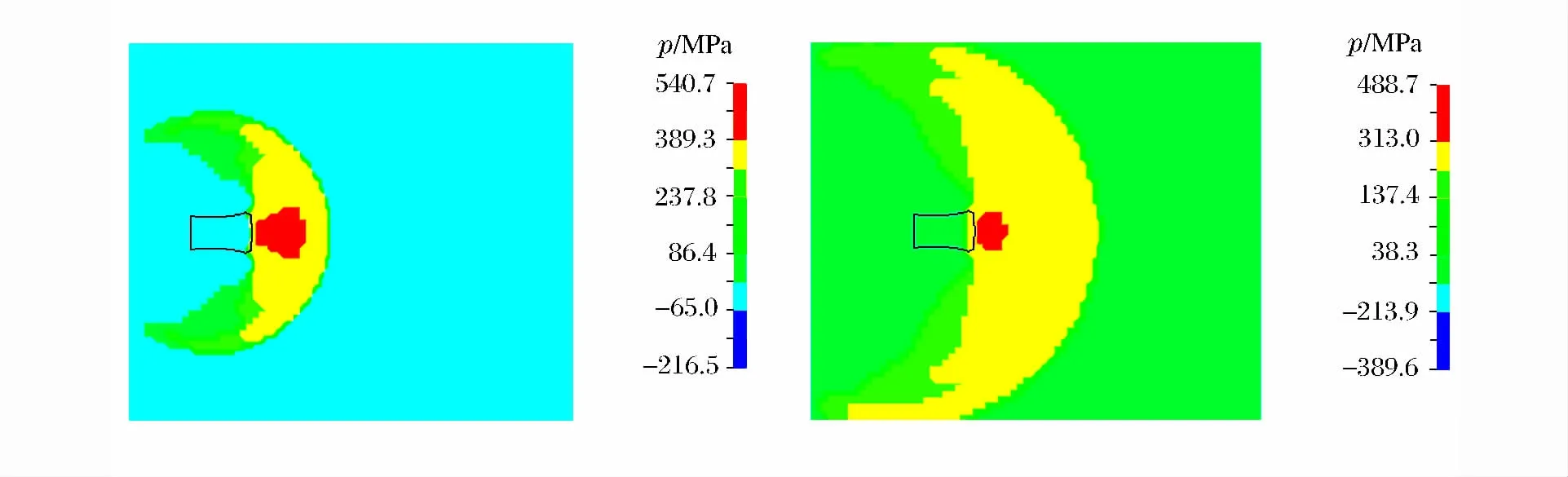
图4 水中冲击波的传播图Fig.4 Shock wave propagation process in water
冲击波常用峰值压力和比冲量来衡量对目标的毁伤作用。水下高速体形成的初始冲击波峰值可达上万个大气压[5],但传播过程中因几何扩散而迅速衰减。在破片初速1 000~2 500m/s的范围内取16个离散点进行计算,得到在1m距离上的冲击波压力峰值pmax,经拟合得图5所示的压力峰值与破片初速的关系曲线。由图5可知,冲击波压力峰值近似随破片初速线性增大。
此外还应清楚,虽然冲击波在传播过程中衰减很快,但对鱼雷等典型水中目标的电子元器件来说,其作用不可忽视。比如鱼雷壳体内部安装有大量的功能元件,这些功能元件的抗冲击能力较差,很容易因遭受冲击而功能失效,导致鱼雷被毁伤而丧失进攻能力。

图5 冲击波压力峰值与破片初速的关系Fig.5 Relation between the peak pressure of the shock wave and initial velocity
2.4 破片侵彻位移及侵彻能力
图6所示为采用有限元分析的速度为100m/s时,破片的侵彻位移随初速度的变化情况,其中散点为数值计算结果,实线为拟合曲线。对积分可得
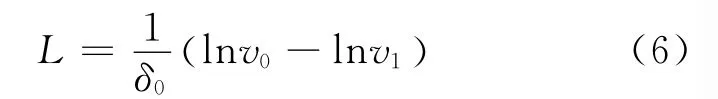
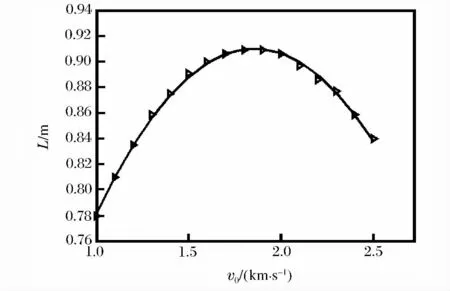
图6 侵彻距离随初速的变化关系Fig.6 Variation of penetration distance with initial velocity
由式(6)可知,破片在水中侵彻距离L与它的速度呈对数关系,在破片形状、质量、剩余速度一定的条件下,侵彻距离应随初速的增大而增大。但在本文中的实验速度范围内,随着速度的增加,破片在水中的侵彻距离先增加,随后有一定程度的降低。由破片的墩粗变形分析可知,破片入水瞬时形成压缩波,当速度达到910~1 115m/s时压缩应力超过了破片材料的动态强度,使破片产生墩粗变形。且随着破片入水速度的增加墩粗变形量加大。在速度较低时,破片的墩粗变形较小,它所引起的破片侵彻能力的变化不能改变破片侵彻距离随速度增大而增加的趋势,破片的侵彻距离随速度递增。随着速度的进一步增加,墩粗变形引起的侵彻距离下降的增量大于速度增大而引起的侵彻距离增加的增量,破片的侵彻能力开始降低。
3 结 论
通过数值模拟方法,建立三维长方体高速破片在水介质中运动的有限元模型,得出如下结论:
(1)高速破片水中运动初期,速度衰减很快;到后期速度衰减放缓。
(2)高速破片入水侵彻初始时刻将受到水的惯性力作用而形成压缩波。对于低碳钢材料破片,当初始速度大于910~1 115m/s时,压缩波强度将大于材料的动态屈服强度而使破片发生墩粗变形。
(3)高速破片形成的初速冲击波压力峰值很大,且随初速的增加而增大。
(4)当破片速度较小时,高速破片的水中侵彻距离随初始速度的增大而增大,当速度达到某一临界值以后,侵彻距离L随初始速度的增大而逐渐减小。
[1]沈晓乐,朱锡,侯海量,等.高速破片侵彻防护液舱试验研究[J].中国舰船研究,2011,6(3):12-15.Shen Xiao-le,Zhu Xi,Hou Hai-liang,et al.Experimental study on penetration properties of high velocity fragment into safety liquid cabin[J].Chinese Journal of Ship Research,2011,6(3):12-15.
[2]白金泽.LS-DYNA3D理论基础与实例分析[M].北京:科学出版社,2005.
[3]吴建萍,魏志芳,李柱.基于LS-DYNA的球形破片侵彻明胶的数值模拟[J].机电技术,2011,1:28-30.Wu Jian-ping,Wei Zhi-fang,Li Zhu.Numerical simulation of spherical fragment penetrating into gelatin based on ANSYS/LS-DYNA[J].Mechanical & Electrical Technology,2011,1:28-30.
[4]Trevino T.Applications of arbitrary lagrangian eulerian(ALE)analysis approach to under water and air explosion problems[R].AD-A384983,2000.
[5]王肖钧,赵新.高速钢球在水中贯穿过程的数值计算[J].爆炸与冲击,1992,12(3):213-218.Wang Xiao-jun,Zhao Xin.Numerical study of a steel ball penetrating in water with high speed[J].Explosion and Shock Waves,1992,12(3):213-218.
[6]Tate A .A theory for the deceleration of long rods after impact[J].Journal of the Mechanics and Physics of Solids,1967,15(6):387-399.

