峰值频率大相关-小残差的弦乐器校音方法*
唐 骏 ,刘 虹
(1.厦门理工学院 通信工程系,福建 厦门 361024;2.厦门大学 信息科学与技术学院,福建 厦门 361004)
0 引言
随着多媒体技术的发展及网络的普及,人们欣赏音乐、获取音乐资源变得十分便捷,而各种乐器也快速走进音乐爱好者的家庭,如钢琴、吉它等。
弦乐器因其物理特性,需要进行定期校正[1-2],以往这项工作一直由经过专业训练的调音师来承担。即便是专业的调音师,也会受生理、心理以及客观环境的影响,从而出现对音准判断的偏差;另外,随着乐器快速普及,少量的专业调音师难以满足广大的需求,乐器校音成为难题[3]。因此,迫切需要一种仪器,可以完全排除调音过程中的主观因素,能够客观准确地校准乐器。
1 基音检测原理与常用算法
校音的根本目的就是精确确定乐音的基频。信号基频的检测根据处理域或方法的不同,主要可分为时域方法和频域方法。
1.1 时域方法
将信号看作时间的函数,其波形反映依时间变化的特性,通过观察信号波形,确定其基本周期,从而获得基频[4]。最常用的有自相关函数法。
自相关函数是信号自身的相关函数,可以度量信号自身的相似性。对于无限长的离散信号x[n],自相关函数的定义为:

式中m为信号的延迟。
对于长度为N的离散信号x[n],自相关函数的定义为:
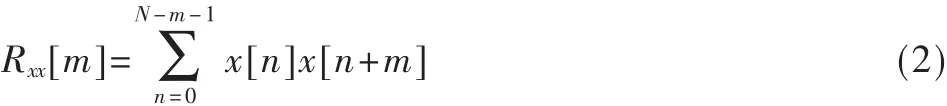
如果序列x[n]是周期的,则其自相关函数也是周期的,且周期相等。
1.2 频域方法
频域有更多的与基频相关的信息。具有基频的信号往往是由频率具有谐波关系的信号组成,因此有很多利用频域信息提取基频的方法[5-6]。
谐波峰值法。谐波峰值法是基于离散傅里叶变换(DFT)的分析法,将信号通过FFT变换得到离散的频谱,确定峰值频率。对于周期信号而言,峰值频率是基波频率的整数倍,如果能确定峰值频率对应的谐波次数,便可以求出基波频率。
离散小波变换法。离散小波变换允许在连续的尺度上将信号分析为高频成分和低频成分,它是时间和频率的局部变换,能有效地从信号中提取信息。
2 PFMCMR算法流程
PFMCMR算法框图如图1所示。输入音频信号先进行端点检测[7-8],目的是去除噪声和静音段,以便仅对有用信号段进行分析,有用信号段加窗后进行傅里叶分析。设采样频率为 Fs,窗长为 N,则 FFT的谱线间隔为Δf=Fs/N,一般这样的精度离实际要求相差甚远,因此需要通过频率细化算法,以求得精度更高的峰值频率。细化的频率间隔可由具体算法的参数控制,根据实际需要精确到约千分之几赫兹即可。
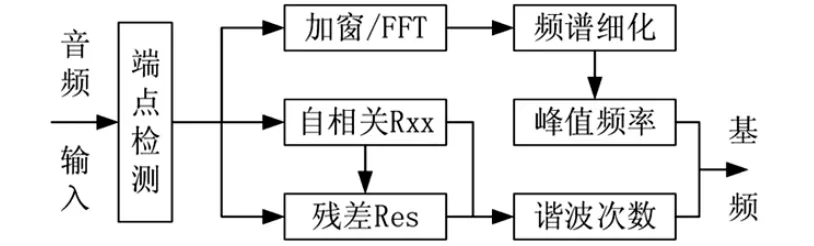
图1 PFMCMR算法框图
由前述可知,利用信号的自相关函数可以确定其基本周期,但由于实际信号的衰减、起伏及受噪声影响等诸多因素,相关函数的峰值未必出现在基波周期处,更多时候出现在基波周期整数倍附近[9]。因此,直接将相关函数峰值的位置确定为基本周期既不可靠,精度也无法满足实际需求。尽管如此,自相关函数为确定峰值频率对应的谐波次数提供了有用的信息。
自相关反映的是信号结构的某种自相似程度,弦乐器音色丰富,音的结构多变,所以,仅依据自相关函数来确定基波周期往往会导致倍频或分频。为了更准确地确定峰值频率对应的谐波次数,PFMCMR算法结合信号移位、相减后的残差幅度值。自相关函数为计算残差时的移位量提供了有用信息。
自相关函数的局部最大值和残差幅度局部最小值相结合,可以有效地确定峰值频率对应的谐波次数,从而最终计算出基频。
3 PFMCMR算法的具体实现
为了方便定量叙述,取定一些参数如下:采样频率Fs=44 100 Hz,窗长N=4 096点。FFT谱线间隔为Δf=Fs/N=44 100/4 096≈10.77 Hz。为了得到高精度的峰值频率,可以采用频率局部细化算法,如ZoomFFT或 CZT[10],本文采用后者。PFMCMR算法的具体实现步骤如下:
(1)先计算FFT谱线幅度的最大值,其对应的索引记为idxMaxFFT,从而可以确定峰值频率一定在idx-MaxFFT-1~idxMaxFFT+1对应的频率范围内;
(2)取 idxMaxFFT-1~idxMaxFFT+1频率范围进行频率细化,细化的倍数由CZT计算的频率间隔数M决定,一般取 M=N,因此,细化后的频率间隔为 ΔfM=2Fs/N2≈0.005 Hz;
(3)计算细化后的峰值频率Fp,与之对应的周期记为Tp;
(4)计算一帧信号的自相关函数 Rxx[m],并求其峰值Rmax,对应的索引 m记为 idxMaxR,根据实际情况,在搜索相关函数最大值时,需要排除Rxx[0]附近的数点;
(5)计算 Rxx[kTp],其中 k为正整数,且 kTp≤idxMaxR,如果Rxx[kTp]/Rmax>THR,则 kTp作为基波周期的候选值,记为kiTp,i为整数,其最大值为基波周期的候选值的数目,其中THR为一阈值,本文取0.85;
(6)以kiTp为延迟点数,计算残差幅度的平均值:
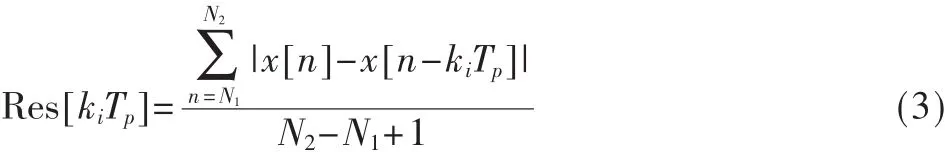
其中 N1、N2为非负整数。
因为峰值频率一定是基频的整数倍,所以基波周期T0一定是 kiTp中的某一个值,Rxx[kiTp]越大、Res[kiTp]越小,则kiTp为T0的可能性越大。所以引入参数:
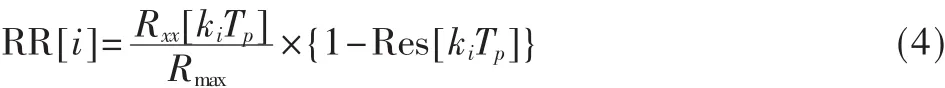
RR[i]越大,kiTp为T0的可能性越大,但由于实际信号的起伏多变,直接利用RR[i]作为参考值会造成一定概率的误判,需要作一些置信修正,即 RRM[i]=RR[i]·T[i],其中T[i]为置信因子,随着i的增大而减小。最后求RRM[i]最大值,其对应的i记为idxMaxRRM即为峰值频率对应的谐波次数,所以,基频F0=Fp/idxMaxRRM。
4 测试与性能分析
校音软件两个最重要的指标是精确度和准确度,为了测试精确度,采用单音正弦信号和定音器生成的标准音作为测试对象。用吉它和钢琴音进行整体性能测试。正弦单音由软件生成,定音器的音、吉它音和钢琴音采用现场录制的方式。定音器 A3、吉它 G3、钢琴 B3音的时域波分别如图 2(a)、2(b)和 2(c)所示。
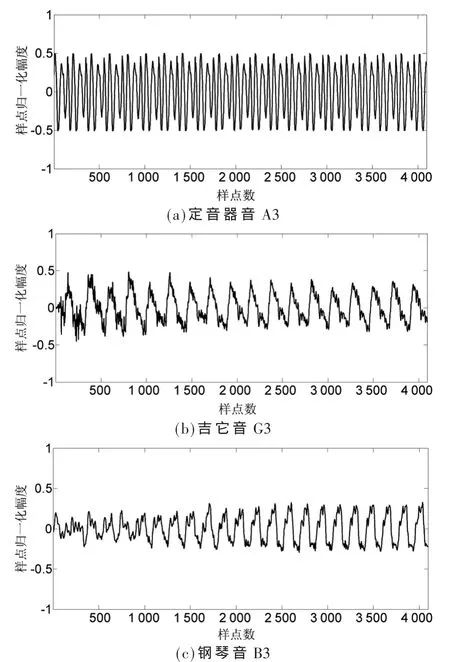
图2 时域波形
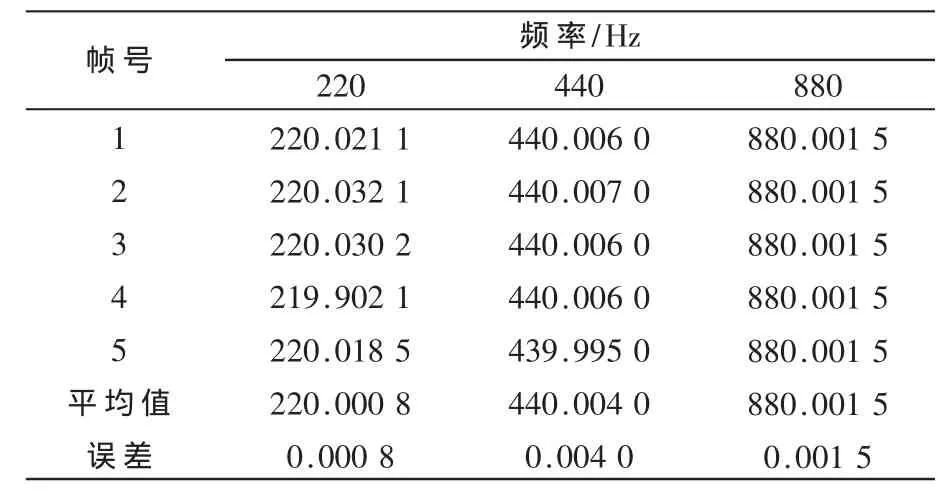
表1 单音正弦测试结果
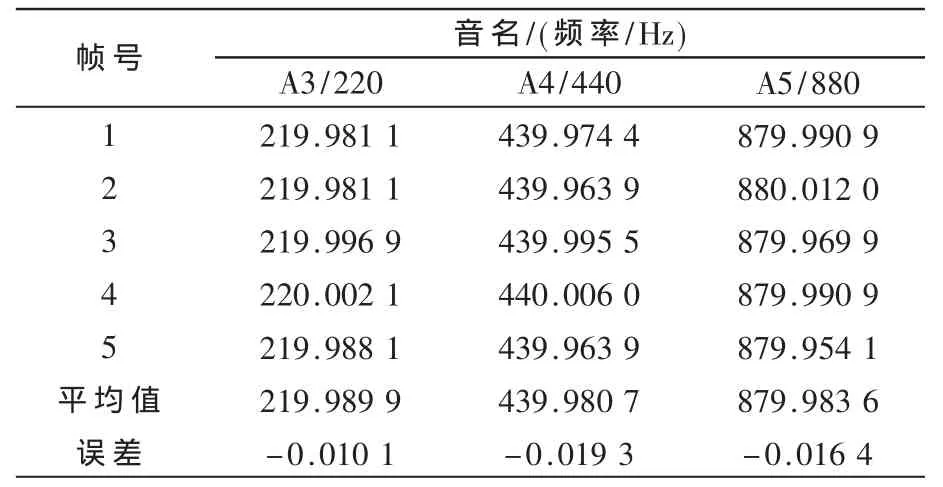
表2 定音器测试结果
表1、表2分别为单音正弦和定音器的测试结果。可以看出,对于单音正弦信号,实测精度和理论分析相符合,误差均在0.005 Hz以内。相比而言,定音器的测试误差要略大,这是因为音频信号在采集过程中会发生失真。即便如此,精度仍在0.1 Hz以内。
表3、表4分别为吉它和钢琴3个音的测试结果。可以看出,每个音的误差和标准差均未超过0.2 Hz。
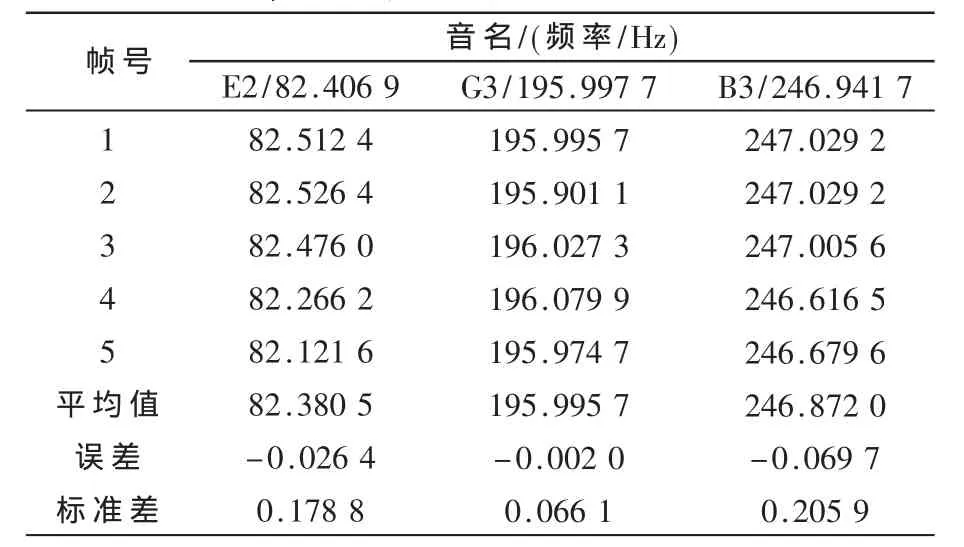
表3 吉它音测试结果
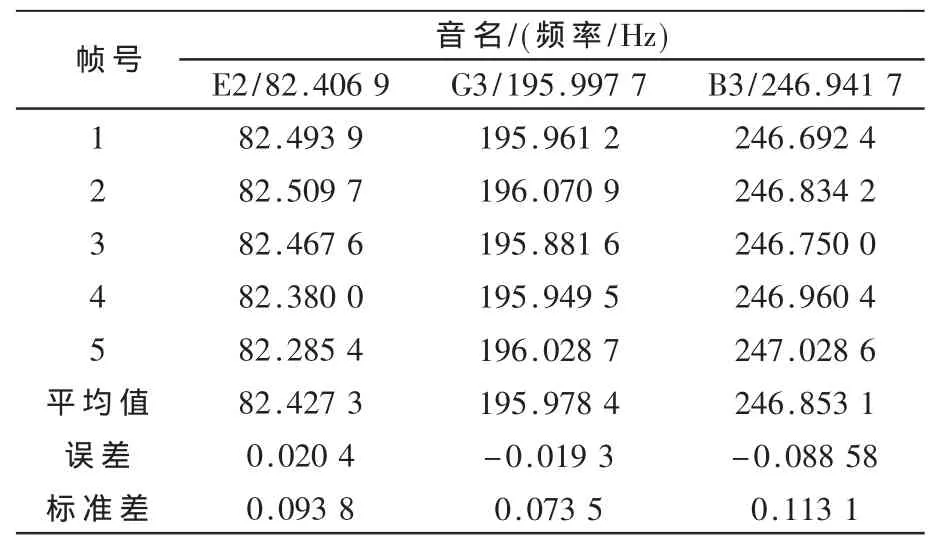
表4 钢琴音测试结果
综合表1~表4的测试结果,表明PFMCMR算法具有高精度和良好的稳定性,完全满足实际应用的要求。
5 结束语
本文针对弦乐器校音的基本问题,介绍了乐音基频检测的常用算法,并分析了这些算法的局限性。为了解决基频检测的精度和稳定性问题,本文提出了一种基于弦乐器音频信号时频特性的校音新算法。利用频谱细化方法得到高精度的谐波峰值频率,时域中结合信号的相关函数和信号残差,基于相关局部最大和残差局部最小原则确定基波周期,从而计算出精确的基波频率。测试结果表明,该方法精度高,稳定性好,满足实际应用。
[1]FLETCHER N H,ROSSING T D.The physics of musical instruments[M].Springer,1998.
[2]SETHARES W A.Tuning,timbre,spectrum,scale[M].London:Springer,2005.
[3]潘阳.钢琴校音计算机软件的设计[D].合肥:安徽大学,2011.
[4]AMADO R G.Pitch detection algorithms based on zero-cross rate and autocorrelation function for musical notes[C].Audio,Language and Image Processing,2008,ICALIP 2008,International Conference on,IEEE,2008:449-454.
[5]BENETOS E,DIXON S.Joint multi-pitch detection using harmonic envelope estimation for polyphonic music transcription[J].Selected Topics in Signal Processing,IEEE Journal of,2011,5(6):1111-1123.
[6]RIGAUD F,DAVID B,DAUDET L.A parametric model and estimation techniques for the inharmonicity and tuning of the piano[J].The Journal of the Acoustical Society of America,2013,133(5):3107-3118.
[7]KHOA P C.Noise robust voice activity detection[D].Singapore:Nanyang Technological University,2012.
[8]MA Y,NISHIHARA A.Efficient voice activity detection algorithm using long-term spectral flatness measure[J].EURASIP Journal on Audio,Speech,and Music Processing,2013,2013(1):1-18.
[9]BROWN J C,VAUGHN K V.Pitch center of stringed instrument vibrato tones[J].The Journal of the Acoustical Society of America,1996,100(3):1728-1735.
[10]MARTIN G.Chirp Z-transform spectral zoom optimization with MATLAB[Z].Sandia National Laboratories Report SAND2005-7084,2005.