基于智能决策的火箭安控系统*
李 娅,张建勋,肖朝晖
(重庆理工大学 计算机科学与工程学院,重庆 400050)
0 引言
随着航天事业的不断发展,火箭发射成为世界各国所关注的焦点。然而火箭发射是一项复杂的任务,经常发生故障,落点将超出允许落点范围而危及地面安全时,必须加以控制,终止火箭动力飞行并将其炸毁。如果不能准确控制,造成的后果是非常严重的。因此火箭发射的安全控制成为世界各国需要解决的首要问题[1-2]。
火箭飞行安全控制系统一般由地面控制系统和火箭控制系统组成[3]。其中,地面控制系统主要观察火箭飞行状态并对其进行判断,发出相应的报警或炸毁指令;火箭控制系统接收地面系统发来的炸毁指令,经过判断分析,点燃爆炸器。结合这两个控制系统各自的特点,构建的火箭安控系统要求具有极高的可靠性、实时性,所采用的安全控制信息要有很高的精度,才能对火箭的飞行状态进行实时诊断,及时有效地做出判断,为安控领域专家的最终决策提供支持发挥着重要作用。
传统的火箭安全控制系统是在确定性的安控知识的基础上,通过简单的逻辑判断推理,得出安控决策方案。这种方法经常产生错误的报警,导致安控专家做出错误决策。本文针对火箭安控知识的特点及现有系统存在的不足,采用人工智能领域的智能决策技术和推理技术,融合安控决策知识,提出了基于智能决策的火箭安控系统,并给出了相应的系统模型。通过对两个安控系统的比较分析表明,该智能决策系统能够更加准确地对火箭的发射状态进行观测,及时迅速地得到火箭发射过程中的各种状态,更加有效地对其进行控制决策。
1 安控系统结构
火箭安全控制决策系统是一个集弹道数据处理和安全控制决策于一体的计算机决策支持系统,具体处理流程如下:计算机对各种测量设备提供的实时弹道数据进行实时处理,从中选择可靠性最高的一条弹道,并进行落点计算;然后将计算结果与事先所存储的理论弹道数据进行比较。当偏差值在故障线范围内时,认为火箭飞行正常;当实际参数值达到或超过故障线范围时,根据安控知识库进行推理决策,判断火箭是否处于不安全的故障状态,此时通过计算机向发射指挥控制中心发出告警信号;当安判结论达到允许炸毁线,且预测的故障火箭落点已进入保护区边界线时,则发出炸毁指令;当实际参数值达到必炸线时立即发出炸毁指令。除由地面进行安全控制外,火箭上的安全自毁系统也将每一瞬间的实际参数值与预先输入的规定值加以比较。当超出允许值时,一般先使航天员脱离火箭,解除保险,接通延时装置,以便地面安全分系统选择炸毁时机或落点,而在预定的迟滞时间内,即使地面没有发出炸毁指令,延迟时间一到也要自动起动爆炸装置将火箭炸毁。
基于这种处理流程,安控系统的框架结构如图1所示。该框架结构主要包括四个部分:弹道选择、落点计算与选择、安控知识库和安控推理决策。其中弹道选择、落点计算与选择是弹道数据处理部分;安控知识库和安控推理决策是安全控制决策部分。
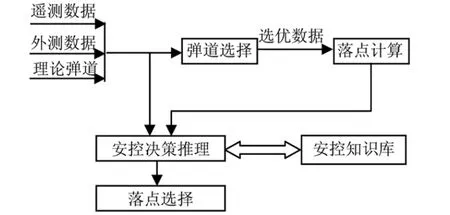
图1 安控系统框架结构
(1)弹道选择
弹道选择首先根据火箭弹道特点的先验知识把测量所得的弹道数据(包括外测数据和遥测数据)与事先所存储的理论弹道数据进行比较,判断其可靠性,剔除误测弹道;然后再根据各测量设备的精度,在可靠性的基础上选用测量精度最高的一条弹道[4],用于落点计算与安全判断。其中理论弹道的数据值可根据在特定时间点的插值来获取;遥测数据和外测数据均可从调用模块中获得。
(2)落点计算与选择
落点计算是在任务实施中瞬时计算出火箭在飞行中的任何一点上的状态,如果发生故障,它落在地面上的位置为安全控制提供依据。落点计算的输入量由测量设备测得的数据经计算机计算后,提供给落点计算的弹体在发射坐标系中的参数,具体包括位置参数:Xk、Yk、Zk和速度参数vxk、vyk、vzk。输出量则是火箭在轨道上瞬时任一实测点的速度值、速度倾角、偏航角、当地高度、星下点经纬度、落点经纬度、落点射程、沿射向的射程、射程偏航量等。
弹道选择、落点计算与选择作为弹道数据处理部分,为安全控制决策提供了数据基础。
(3)安控知识库
安控知识库是安控决策系统工作的基础,用来描述火箭安控系统中的各种知识和规则,由安控参数、原子事实和规则知识库3个表的形式组织起来[3]。这样不仅简化了知识库,便于知识库中知识的组织和管理,而且避免知识的相互交叉,保证了知识的相容性和完整性。
(4)安控决策推理
安控决策推理由定性的知识推理和不确定的推理模型构成。安控系统推理采用基于不确定知识表示的决策网络,在安控推理决策过程中,推理机根据安控知识的特点,通过正向推理机制和深度优先搜索策略进行推理,最终给出基于智能决策的火箭安控系统。
2 安控知识库
2.1 安控知识的分类
在安控系统中,领域专家所给的安控知识复杂,影响因素众多,如果把这些安控知识不加区分地表示出来,一方面增添了知识表示的复杂性,另一方面也给安控知识的推理带来了困难。针对这一难点,系统把安控知识进行了分类,把它分为安全控制参数(简称安控参数)、原子事实和规则知识库3类。
(1)安控参数
安控参数主要是描述火箭安控系统中所用到的参数,可以分为3类:外测弹道落点、遥测弹道落点、遥测压力参数。其中外测弹道落点和遥测弹道落点都包括落点、速度、偏角、倾角、射程等几类参数[3];而遥测压力参数包括俯仰角偏差、滚动角偏差、偏航角偏差、一级压力1、一级压力 2、一级压力 3、一级压力 4、二级压力几个参数。只有落点、速度、射程参数同时参与炸毁和告警,其他参数仅参与告警而不参与炸毁报警。
在每个采样周期都进行安控参数的形成,作为安控系统判断决策的依据。由于在具体实现中,参数的提供不是很完全(仅有飞行的位置和速度数据),而且没有管道数据,这些都为完整的测试增加了困难。在实际实现中系统只好采取一种随机产生安控参数的办法。
(2)原子事实
原子事实主要描述各个状态变量是否连续多点越界的信息。 一般以这种 Si(Y,Vk,20,Z)形式表示,其含义是遥测(Y)弹道速度(Vk)连续 20点超越炸毁线(Z),用来表示规则知识库中的一个前提条件或者结论。其实则是方便进行安全判断的推理而提出的中间变量。
(3)规则知识库
规则知识库主要描述火箭安控系统中的规则知识,由多个原子事实组成,采用才产生式的表示形式,如下所示:

在此产生式中,前提条件 S1和 S3,结论Sy都是以 Si的形式来表示,为原子事实。如果某条规则的前提条件多于两条,则可以引入中间变量,再把规则分成两条来进行存贮;如果某条规则的前提条件少于两条,则可以在前提2处输入一个9999或其他的代码来表示此条前提无效,此时就只有一条前提。
在安控系统中,所得到的安控知识往往是不精确的,因此系统要在产生式表示的基础上,具体采用不确定的知识表示形式[5-6],如下所示:
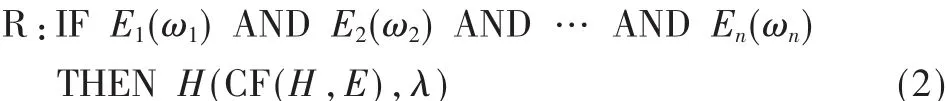
式中,Ei是规则的前提条件,ωi是规则各前提条件的权值(∑ωi=1),H 是结论,CF(H,E)(0<CF(H,E)≤1)是规则的可信度,λ(0<λ≤1)是规则可否应用的阈值[5]。只有当规则所需的前提条件可信度CF(E)≥λ时,相应规则才会被激活,推理相应的结论 H,它的可信度 CF(H)可用如下公式计算:

式中,“*”表示“取极小”运算。
如果式中前提条件E由多个前提条件Ei组成,则有
如下公式:

产生式(2)的表示形式,可以用不确定性知识表示,
如下所示:

经安控系统弹道数据处理部分可以得到S1可信度CF(S1)=0.8,S3可信度 CF(S3)=0.6。
由式(4)可得:
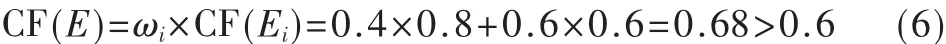
规则被激活,结论H的可信度由式(3)得:
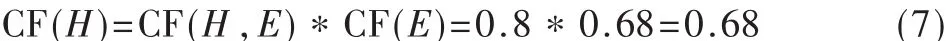
根据上面的知识分类,系统把安控知识用表Para、表Atom、表Rule的形式组织起来,如图2所示。这样不仅简化了知识库,便于知识库中知识的组织和管理,而且避免知识的相互交叉,保证了知识的相容性和完整性。
2.2 安控决策网络的形成
根据安控知识的分类及不确定性的知识表示形式,其决策过程可以用一个与/或树来表示,即用逻辑或门“OR”和逻辑与门“AND”来表示,建立相应的安控决策网络[7-8]。以部分安控规则(如表1所示)为例,建立如图3所示决策网络。
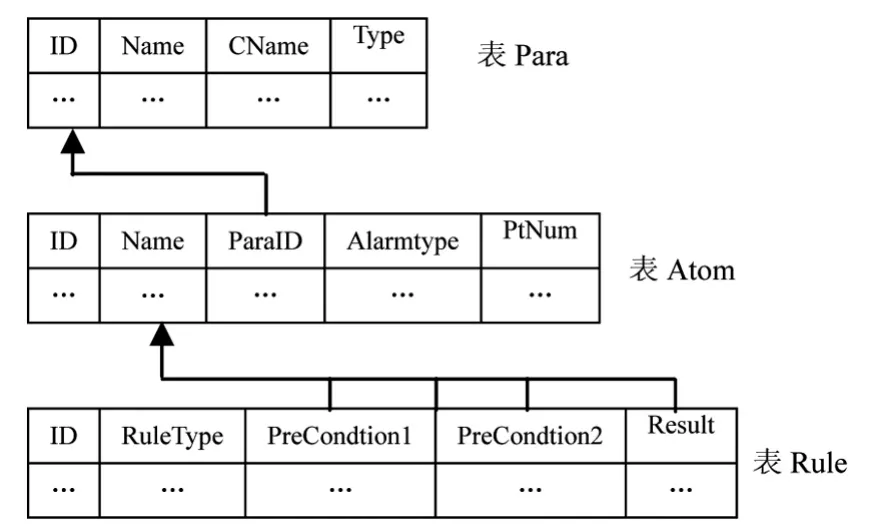
图2 安控知识逻辑关系图
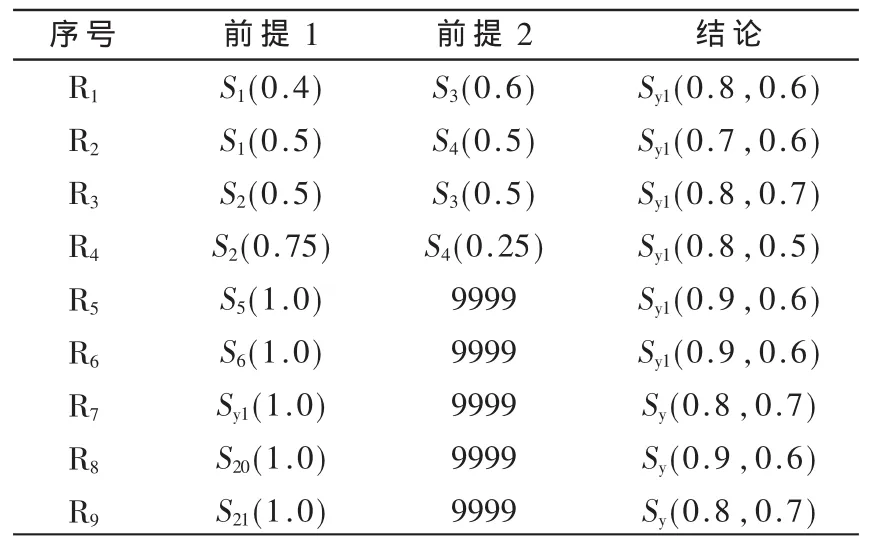
表1 安控规则表
表 1中,“9999” 表示此条前提无效,此规则就只有一条前提。
在图3的决策网络中,为了使网络结构层次明显,便于推理决策, 引入了 S13、S14、S23、S24几个中间变量结点。
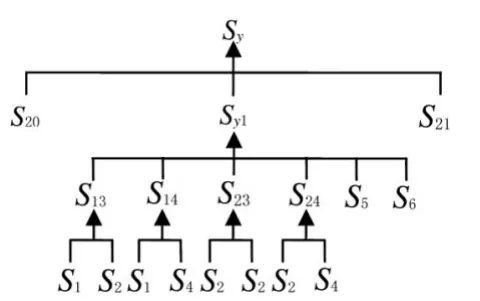
图3 安控决策网络
3 安控推理流程
结合安控知识的特点及相应的决策网络,以Visual C++6.0为开发平台,构建了安控推理决策模型[9],如图4所示,具体的安控推理流程如图5所示。
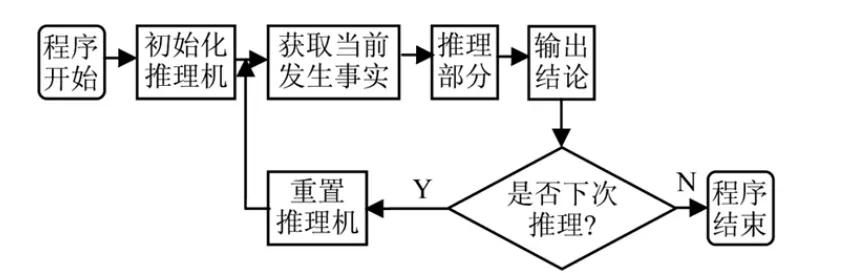
图4 安控推理模型
(3)结合上述安控推理流程,采用了面向对象的系统模型,以Visual C++6.0为开发平台,实现了上述安控决策系统。图6给出了该系统的仿真实验结果,包括轨道轨迹的选择、安判结果、落点参数和推理解释四大模块。在具体的实验,显示了X方向弹道的位置轨迹,安判结果显示为外测告警、遥测告警、联合告警及炸毁(催发指令 k1),推理解释给出了“151.980炸毁”,并有相应的解释依据。上述仿真实验结果表明,该系统能有效地进行弹道选择,实时检测火箭的飞行状态,给出相应的安控决策方案,为安控领域专家的最终判断决策提供参考。

图5 安控推理流程图
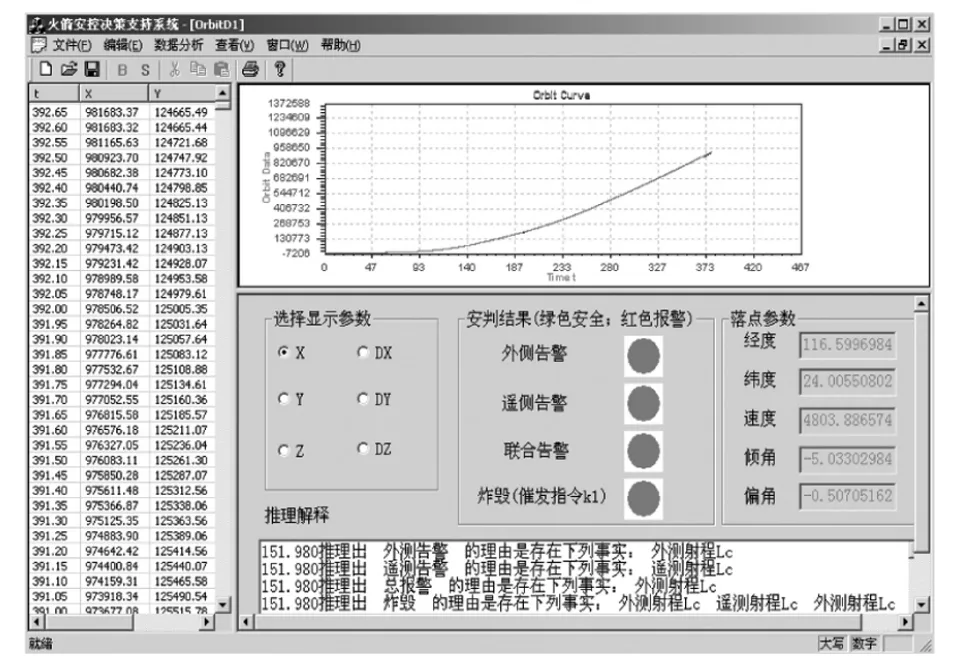
图6 系统仿真运行界面
4 结论
本文针对现有安控系统存在的缺陷和不足,结合数据库技术和人工智能中的推理技术,建立和完善了火箭飞行安全控制决策系统,它是智能决策支持系统在理论和实践上的一个新突破。实验和仿真表明,该系统很大程度上提高了火箭安控系统的准确性和可靠性,能对其进行有效的管理。
[1]张庆振,李清东,任章.基于故障模式分析的运载火箭发射决策系统推理技术研究[J].航天控制,2006,24(3):81-83.
[2]Probabilistic Risk Assessment of the Space Shuttle.A study of the potential of losing the vehicle during nominal operation[R].(NASA-CR-197808).New York:Science Application International Corporation,Advanced Technology Division,28 February,1995.
[3]李娅,张建勋,杨欣.不确定推理模型的火箭安全决策系统[J].重庆大学学报(自然科学版),2010,33(10):118-122.
[4]Zhang Xiaokun,Gong Yingkui,Qu Jianghua.An optimal selection model of the satellite lurk orbit[C].Applied Mechanics and Materials,2013,249-250:270-273.
[5]蔡自兴,徐光佑.人工智能及其应用(第二版)[M].北京:清华大学出版社,1996.
[6]黄洪,任卫红,余达太,等.基于故障树的等级测评专家系统模型研究[J].计算机应用研究,2010,27(1):204-208.
[7]Liao Ruijin,Zheng Hanbo,STANISLAW G.An integrated decision-making model for condition assessment of power transformers using fuzzy approach and evidential reasoning[J].IEEE Transactions on Power Delivery,2011,26(2):1111-1118.
[8]Wang Jianqiang,Nie Rongrong,Zhang Hongyu.Intuitionistic fuzzy multi-criteria decision-making method based on evidential reasoning[J].Applied Soft Computing Journal,2013,13(4):1823-1831.
[9]ONG D C C,KHADDAJ S,BASHROUSH R.Logical reasoning and decision making[J].Proceedings of 2011,10th IEEE International Conference on Cybernetic Intelligent Systems,CIS 2011,2011:26-31.