两类积分的求解*

姜培华，吴 玲，纪习习

(安徽工程大学数理学院，安徽 芜湖 241000)

本文讨论了两类积分的简便求解问题，两类积分如下:

1 积分(1)的求解

对于上述积分(1)若直接考虑一重积分的方法求解，实属不易，因为对于这样的被积函数很难利用凑微分法和分部积分法来解决，为此只好另辟蹊径．本文下面考虑四种办法来解决此问题．

首先给出下面的引理1．

引理1 对于实数a∈R+下述积分等式成立:

证明 (ⅰ)给定下述三个平面区域:D1⊂D2⊂D3，其中:

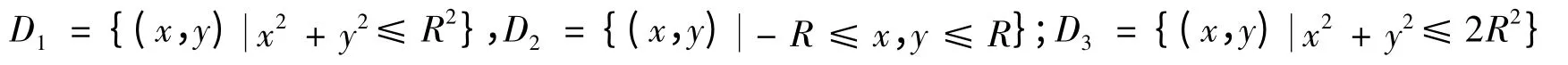
L3=(1－e－2aR2)．又因当R→+∞时由夹逼准则可知当R→+∞时，有从而可得结论(ⅰ)成立．

(ⅱ)给定下述三个空间区域:Ω1⊂Ω2⊂Ω3，其中:

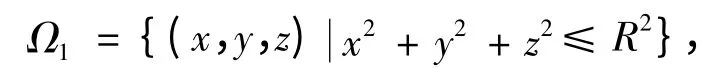
1)二重积分法

考虑到I2并利用引理1的结论(ⅰ)可得:

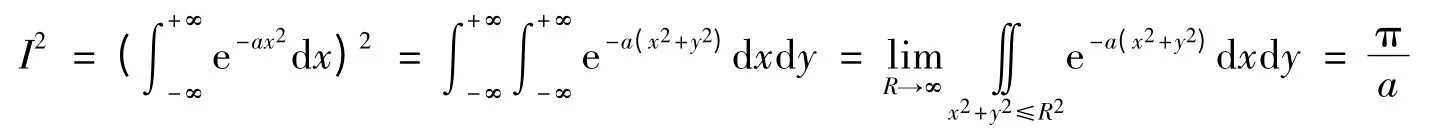
2)三重积分法

考虑到I3并结合引理1中的结论(ⅱ)可得:

即有:

3)伽玛函数法

首先给出伽玛函数的定义和性质，其定义和性质在诸多文献［1，2］中都有介绍．称以下函数

为伽玛函数，其中参数α＞0．伽玛函数具有如下性质:

下面求解此积分:

令y=x2对式(4)作变换可得:

式中z=ay．

4)概率方法

构造正态随机变量X～N(0，1/2a)，则其密度函数为:

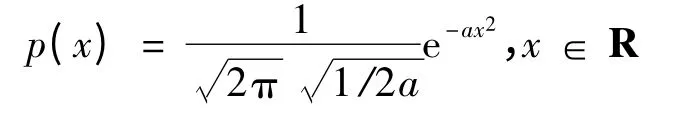
对于积分(1)推广到如下形式:

综上可以看出对于积分(1)考虑到被积函数的形式特点和积分区域的特性，运用概率方法，构造一个适当的概率密度去求解积分，比运用代数方法和分析方法求解要简洁明了．它使数学的不同分支之间架起了桥梁．

2 积分(2)的求解

对于积分(2)很容易看出其是一个定积分，与积分(1)有很大的区别，其积分上下限都是有限值．在这种情况下如果再利用二重积分法、三重积分法和伽玛函数法都不能够解决，为此考虑用概率方法并结合查标准正态分布的概率分布表来解决．

记X～N(0，1)，其概率密度函数和分布函数分别记为φ(x)和Φ(x)．根据积分(2)中被积函数的特点可以构造一个非标准的正态密度函数来表示积分(2)，考虑到积分(2)的积分限都是有限数，进而可以利用正态分布的标准化来查概率分布表求解．基于上述分析可得:

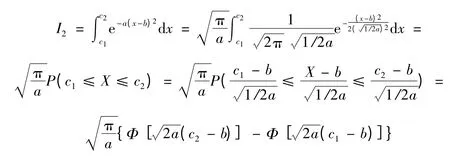
式中X～N(b，1/2a)．

当参数a，b，c1，c2已知时，可以通过查标准正态分布的概率分布表来计算该类积分．

3 应用举例

例1［3］证明不等式:

证明 设X与Y独立同分布于标准正态分布N(0，1)，记区域D1，D2分别为:

易知D1⊂D2，故有P{(X，Y)∈D1}＜P{(X，Y)∈D2}，考虑到X与Y独立即有:

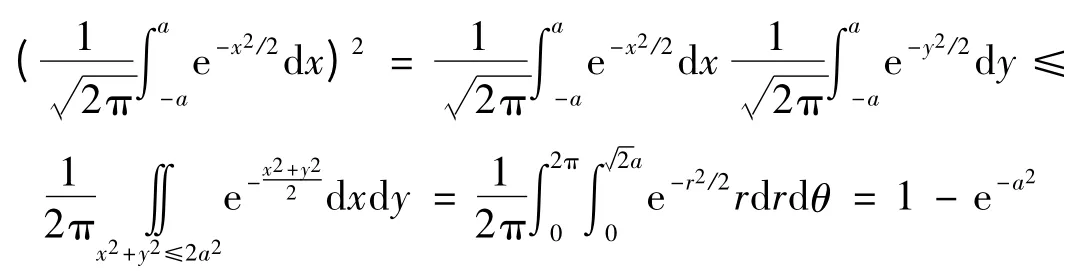
例2［4］已知X，Y相互独立，X～U(0，1)，Y的概率密度为fY(y)=，y＞0，设a的二次方程a2+2Xa+Y=0，求其有实根的概率．

解 由独立性可求出(X，Y)的联合概率密度函数为:

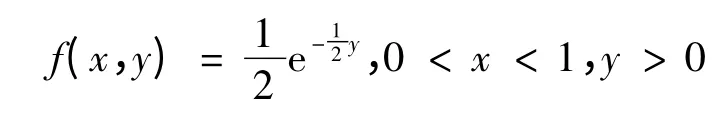
由韦达定理可知方程有实根的概率为:

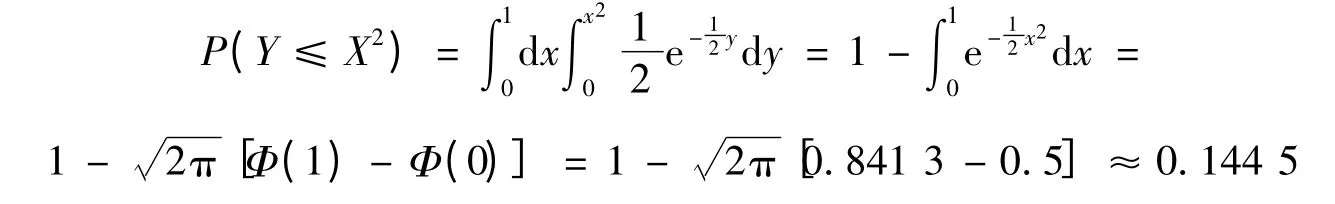
［1］同济大学应用数学系．高等数学(上)［M］．第5版．北京:高等教育出版社，2002．

［2］茆诗松，程依明，濮晓龙．概率论与数理统计教程［M］．北京:高等教育出版社，2004．

［3］Peter－Bickel J．数理统计—基本概念及专题［M］．李泽慧，李效虎，荆炳义，译．兰州:兰州大学出版社，2005．

［4］项立群，汪晓云，梅春晖，等．概率论与数理统计［M］．北京:北京大学出版社，2011．