一类具有集值映射的集值变分包含问题的解的存在性

谷桂花，吴梅花

( 内蒙古民族大学 数学学院，内蒙古 通辽028043)

集值变分包含问题在数学理论和应用中起着非常重要的作用．设B 是一个具有对偶空间B*的实Banach空间，‖·‖和〈·，·〉分别表示B的范数和B与B*之间的对偶对． CB(B)表示B的一切有界闭子集族，H(P，Q)为CB(B)上的Hausdorff 度量，J:B→2B*和J*:B*→B＊＊分别是B和B*上的正规对偶映射．

在文献［1］中给出一类p－η－映射的概念及其性质．在文献［2］中研究了如下集值变分包含问题:对给定的f∈B*，求使得，文献［3］研究了一类具有(p，η)映射的集值变分包含问题．

定义1［2］设η:B×B→B*，p:B→B*，g:B→B是单值映射．

1)称p为η－增生的，如果存在jη(x，y)∈J*η(x，y)使得:〈p(x)－p(y)，jη(x，y)〉≥0，∀x，y∈B．

2)称p为σ－强η－增生的，如果存在jη(x，y)∈J*η(x，y)和σ＞0 使得:

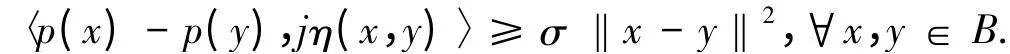
3)称η 为τ－Lipschitz 连续的，若存在τ＞0 使得:

定义2［2］设η:B×B→B*，p:B→B*是单值映射，称集值映射为:

1)η－增生的，如果存在jη(x，y)∈J*η(x，y)使得:

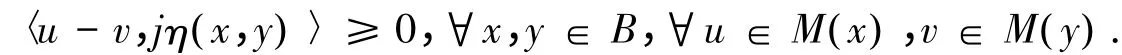
2)p－η－增生的，若M是η－增生的，且对∀ρ＞0 有

定义3［2］映射为单值映射，集值映射M:B→2B*为p－η－增生的，M的预解算子被定义为

其中ρ＞0 的常数．

引理1［2］设映射p:B→B*为σ－强η－增生的，η:B×B→B*为τ－Lipschitz 连续，集值映射M:B→2B*为p－η－增生的，则映射是连续，即:

定义4［4］称映射在第一变元是α－Lipschitz 连续，如果存在α＞0 使得∀y1，x1，x2，…，xp∈B有:

定义5［5］称映射C:B→B为m－H－Lipschitz 连续，如果存在m＞0，使得:

其中H为CB(B)上的Hausdorff 度量．

引理2［5］设B是实Banach 空间和J:B→2B*是正规对偶映射，则∀x，y∈B有:

1 主要结果

下面证明集值变分包含问题(1)的解的存在唯一性．

定理1 设B是实Banach 空间，单值映射p:B→B*为σ－强η－增生的，g:B→B为γ－Lipschitz 连续，g－I是s－强增生的，映射p·g为δ－Lipschitz 连续单值映射Ai:B→B为hi－Lipschitz 连续(i=1，2，…，p)，η:B×B→B*为τ－Lipschit 连续，映射分别在第i变元是αi－Lipschitz，βi－Lipschitz 连续，集值映射D:B→分别为m－H－Lipschitz 连续，mi－H－Lipschitz 连续(i=1，2，…，p)，令M:B×是集值映使得对每一固定的是p－η－增生的，并且dom(M(·，w))≠φ，假设存在正数μ，ρ 满足条件:

则变分包含问题(1)在B中有唯一解．

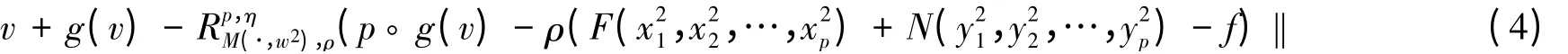
由引理2 及g－I的s－强增生性，有:

即

因此，u∈B是集值变分包含问题(1)的唯一解．证毕．

注:文献［2］中的结果是本文的特殊情形．

［1］ 吴梅花．一类p－η 映射及其性质［J］．内蒙古民族大学学报:自然科学蒙文版，2011，43(1):1－3．

［2］ 吴梅花．一类集值变分包含问题解的存在性［J］．内蒙古民族大学学报:自然科学汉文版，2010，25(2):127－129．

［3］ 吴梅花．一类具有(p，η)映射的集值变分包含问题［J］．湖北民族学院学报:自然科学版，2014，32(3):297－299．

［4］ Jian W P．On a new system of generalized mixed quasi－variational－like inclusions with (H，η)－Accretive operators in realq－uniformly smooth Banach spaces［J］．Nonlinear Analysis，2008，68:981－993．

［5］ Feng H R，Ding X P．A new system of generalized nonlinear quasi－variational－like inclusions with A－monotone operators in Banach Spaces［J］．Journal of Computational and Applied Mathematics，2009，225:365－373．