谈隐枚举法中过滤约束的使用与解题技巧
吴振华 贵文龙 智国建
(桂林电子科技大学商学院,广西 桂林 540114)
1 引言
在整数规划中,隐枚举法(Implicit enumeration algorithm)是用于求解“0-1整数规划问题”的常见方法,其基本思想是通过增加“过滤约束”舍弃一定不最优解的解组合以求得最优解[1]。在教学过程中发现,许多学生存在这样的疑问:过滤约束应如何添加?作用何在?为此,本文通过实例阐述隐枚举法的求解步骤、过滤约束的作用及“隐”字的含义,帮助学生更好地掌握隐枚举法。
2 目标函数求max的0-1规划问题求解
[例1] 求以下0-1整数规划问题的最优解?
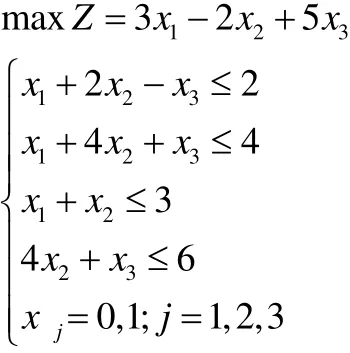
求解步骤[2]:
(1)寻找目标函数值下界。可以判断,当可行解X = (0,1, 0)T时,该问题的目标函数值(-2)最小,因此可以确定目标函数值下界,即3x1-2x2+ 5x3≥-2。
(2)构造过滤约束,并将其加入到原约束条件中。
因函数函数值大于等于“-2”,因此可能是0[X =(0, 0,0)T)]、3[X =(1,0,0)T)]和 5[X =(0,0,1)T)]等,可先构造过滤约束“3x1-2x2+ 5x3≥0”,则原模型变为:

(3)写出所有解组合,比较目标函数值 Z,并检查是否满足约束条件和过滤条件,得出最优解。过滤约束为“3x1-2x2+ 5x3≥0”的求解过程如表1所示:
当X =(0,0,0)T时,满足所有约束条件(包括过滤约束),因此在表中对应位置添入“√”,此时目标函数值Z为“0”。当X =(0,0,1)T时,满足所有约束条件,因此在表中对应位置添入“√”,此时目标函数值Z为“5”。当X =(0,1,0)T、(0,1,1)T和(1,0,0)T时,Z值分别为“-2”、“3”和“3”,均小于“5”,由于目标函数求最大值,因此无须再去考虑 X是否满足约束条件。当X =(1,0,1)T时,满足所有约束条件,因此在表中对应位置添入“√”,此时目标函数值Z为“8”。当X=(1,1,0)T和(1,1,1)T时,Z值分别为“1”和“6”,均小于“8”,因此可求得该问题的最优解为:X*=(1,0,1)T,Z*=8。
可见,添加过滤约束可以加快筛选过程,“隐”去不可能成为最优解的解组合(见表1加粗部分,下同),以简化求解过程。但需注意,过滤约束一定要选满足原约束条件。同时,为保证解组合不遗漏,可参照“二进制”的表达方法,将所有解依次列出,本题因有三个变量,故解组合的数量为:23=8,详见表1。
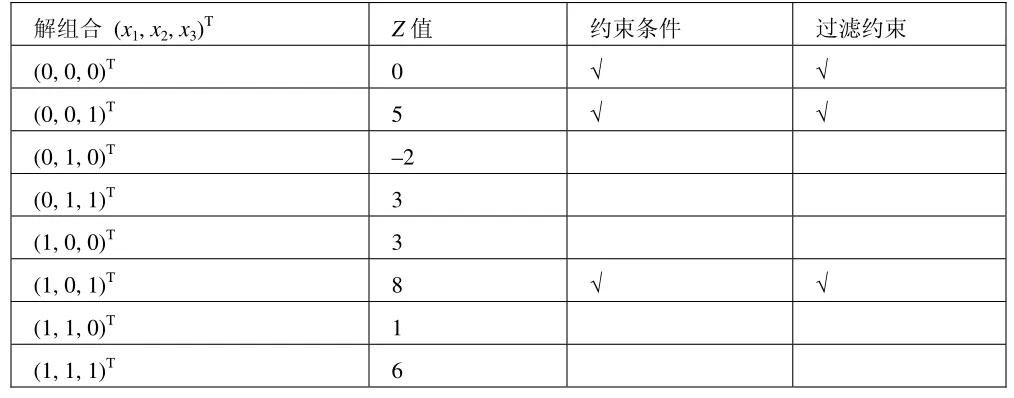
表1 过滤约束为“3x1 -2x2 + 5x3 ≥ 0”的求解过程
同理,可构造过滤约束“3x1-2x2+ 5x3≥3”[X =(1, 0,0)T]和“3x1-2x2+5x3≥5”[X =(0,0,1)T],求解过程见表2。

表2 过滤约束为“3x1 -2x2 + 5x3 ≥ 3”和“3x1 -2x2 + 5x3 ≥ 5”的求解过程
当然,对于本题如果构造过滤约束“3x1-2x2+ 5x3≥ 8”[X =(1,0,1)T],求解过程将更加快捷。因此,在求解目标函数求最大值的“0-1整数规划问题”时,为使求解过程更加简捷,应在多个过滤约束中选取右端常数较大的过滤约束,过滤约束右端项越大求解越方便。
常见求解错误举例:
[例2] 求以下0-1整数规划问题的最优解?[3]

许多学生首先构造过滤约束“4x1+3x2+2x3≥0”[X=(0,0,0)T],然后按步骤求解,过程如表 3所示,求解结果为:X* =(1,1,1)T,Z*=9。虽然求解结果正确,但却犯了一个概念性错误,即 X =(0,0,0)T并不满足原模型约束条件(“4x1+x2+3x3≥3”和“x2+x3≥1”),不能作为过滤约束。同时,求解顺序是从 Z值最小开始依次判断,过程较为复杂。说明,学生并没有掌握隐枚举法的解题技巧。更好的解法是:构造过滤约束“4x1+3x2+2x3≥9”[X =(1,1,1)T],按Z值从大到小的顺序进行求解,即优先考查 Z值较大的解组合,则很快得到最优,过程见表4所示。

表3 过滤约束为“4x1 + 3x2 + 2x3 ≥ 0”的求解过程

表4 过滤约束为“4x1 + 3x2 + 2x3 ≥ 9”的求解过程
3 目标函数求min的“0-1整数规划问题”
对于目标函数求最小值的“0-1整数规划问题”,求解步骤与求最大值时有所区别,应首先寻找目标函数值上界,其它步骤则与求最大值相同。主要技巧是:在可能构造的多个过滤约束中选取右端常数较小的过滤约束,过滤约束右端项越小求解越方便。
[例3] 求以下0-1整数规划问题的最优解?[4]

对于本题(解组合数量为24= 16),可构造过滤约束“2x1+5x2+3x3+4x4≤4”[ X =( 0,0,0,1)T],求解过程如表5所示,求解结果:X*=(0,0,0,1)T,Z*=4。

表5 过滤约束为“2x1 + 5x2 + 3x3 +4x4 ≤4”的求解过程
4 教学体会
对于决策变量较少(如不超过4个)的“0-1整数规划问题”来说,隐枚举法是比较有效的求解方法,其中“隐”字的含义是通过构造过滤约束排除不可能成为最优解的解组合,减少求解过程,快速得到最优解。在使用该方法的时候,需要注意以下三点:首先,判断目标函数“求最大值”还是“求最小值”,以此确定求解顺序是从Z值“最大”还是“最小”开始;其次,辨别所构造的过滤约束是否满足原模型的约束条件;最后,应按“二进制”顺序写出所有解组合,避免遗漏。在初学时,学生可选择两道典型习题(目标函数求“最大和最小”)进行反复练习,以掌握隐枚举法的求解思路和技巧。
[1] 王耀辉,陈超,孙鹏.0-1整数规划及隐枚举法在学生面试问题中的应用[J].中国科教创新导刊,2011,(22):89.
[2] 常大勇.运筹学[M].北京:中国物资出版社,2010.
[3] 谢家平.管理运筹学[M].北京:中国人民大学出版社, 2010.
[4] 熊伟.运筹学[M].机械工业出版社,2005.

