基于统计方法对新疆环境污染的研究——以新疆工业各行业为例

崔金蕾 李国东

(新疆财经大学应用数学学院，新疆 乌鲁木齐 830012)

在经济迅猛发展的同时，环境相应着也发生了变化。环境的污染越来越严重，部分省市出现了严重的雾霾，水体被污染等现象，这危害着人类的生存。尽管政府采取了一定的措施，但是经济的发展对环境的破坏不是一蹴而就的，因此对环境的治理效果也不一定有显著的成效。新疆是一个重工业基地，对产品进行初加工，不可避免的要有大量的废水废气的排放，这就需要对各个行业各个部门有一个详尽的分析，得出工业中对环境的污染最大的行业，对治理有一定的针对性，进行综合治理。

从国内外的文献来看，很多专家学者研究经济的发展对于环境污染的影响，如1991～2011年甘肃省经济增长环境污染研究[1]；各个区域对环境污染的研究，如我国区域城市化与环境污染关系的空间计量研究[2]，河南省产业结构升级与环境污染关系研究[3]等等。本文以新疆工业中各行业为例，现在将用统计的一些方法对工业中废水废气的排放进行分析，得出应加强管理行业类别的结论。

现借鉴《2013年新疆统计年鉴》中的数据，将其整理如下：

行业分为农副食品加工业、食品制造业、酒、饮料和精制茶制造业、纺织业、造纸及纸制品业、石油加工、炼焦及核燃料加工业、化学原料及化学制品制造业、化学纤维制造业、黑色金属冶炼及压延加工业、电力、热力的生产和供应业、其他行业，分别简称为农品加工、食品制造、副食制造、纺织业、纸制品业、燃料加工、原料制造、纤维制造、金属加工、电热产供、其他行业，如表1所示[4]：

表1 工业按行业重点调查工业企业废水废气及污染物排放情况

1 基本原理

1.1 主成分分析基本思想

主成分分析是设法将原来众多具有一定相关性（比如P个指标），重新组合成一组新的互相无关的综合指标来代替原来的指标。主成分分析，是考察多个变量间相关性一种多元统计方法，研究如何通过少数几个主成分来揭示多个变量间的内部结构，即从原始变量中导出少数几个主成分，使它们尽可能多地保留原始变量的信息，且彼此间互不相关。通常数学上的处理就是将原来P个指标作线性组合，作为新的综合指标[5]。

最经典的做法就是用F1（选取的第一个线性组合，即第一个综合指标）的方差来表达，即Var(F1)越大，表示F1包含的信息越多。因此在所有的线性组合中选取的F1应该是方差最大的，故称F1为第一主成分。如果第一主成分不足以代表原来P个指标的信息，再考虑选取F2即选第二个线性组合，为了有效地反映原来信息，F1已有的信息就不需要再出现在F2中，用数学语言表达就是要求 cov(F1,F2) = 0，则称F2为第二主成分，依此类推可以构造出第三、第四，…F…，第P个主成分。

1.2 主成分分析步骤

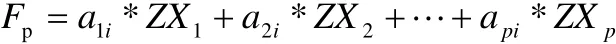
其中 a1i,a2i,… ,api(i = 1, …m)为X的协 方差阵Σ的 特征值所对应的特征向量， ZX1,Z X2, … ,ZXp是原始变量经过标准化处理的值。 A=(aij)p×m=(a1,a2, …am)，Rai=λiai其中，R为 相关系数矩阵，a是相应的特征值和单位特征向量,λ1≥λ2≥… ≥λp≥0。i

其中主成分分析法的计算步骤：

（1）指标数据标准化（SPSS软件自动执行）；

（2）指标之间的相关性判定；

（3）确定主成分个数m；

（4）主成分Fi表达式；

（5）主成分Fi命名。

1.3 聚类分析基本思想

依据研究对象（样品或指标）的特征，对其进行分类的方法，减少研究对象的数目。各类事物缺乏可靠的历史资料，无法确定共有多少类别，目的是将性质相近事物归入一类。各指标之间具有一定的相关关系。

主要的步骤如下：第一步：逐个扫描样本，每个样本依据其与已扫描过的样本的距离，被归为以前的类，或生成一个新类。第二步，对第一步中各类依据类间距离进行合并，按一定的标准，停止合并。

2 结果及其分析

采用SPSS软件及其R软件对新疆工业各行业污染的排放量进行分析。

2.1 主成分分析

（1）主成分的初始结果分析

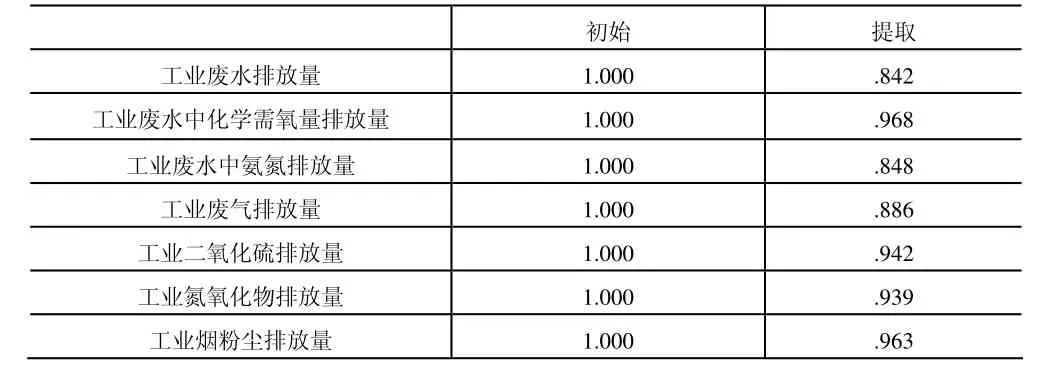
表2 主成分分析的初始结果

根据表2可知，主成分包含指标变量的信息比较接近，其中指标工业废水排放量与工业废水中氨氮排放量信息损失比较大。

（2）主成分的提取

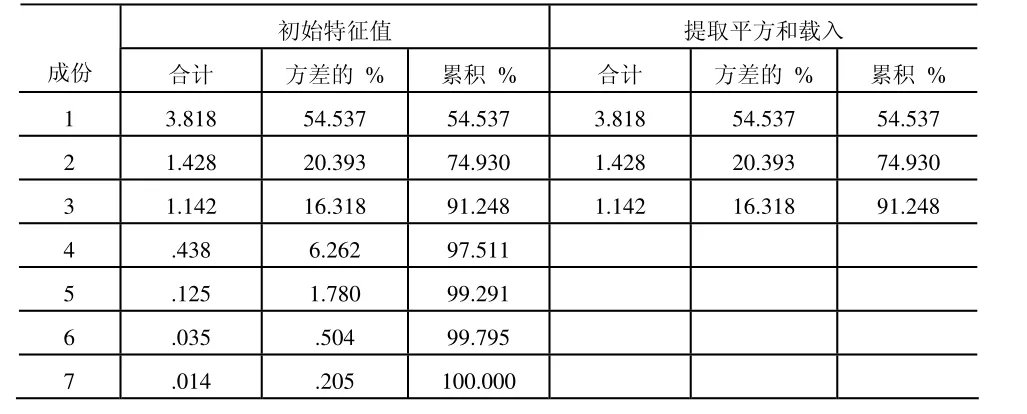
表3 主成分提取表解释的总方差

观察表3，主成分提取表中有三个特征值大于1的主成分，且累积贡献率达到91.248%，所以提取三个主成分比较合适。用碎石图直观的表示为图1：

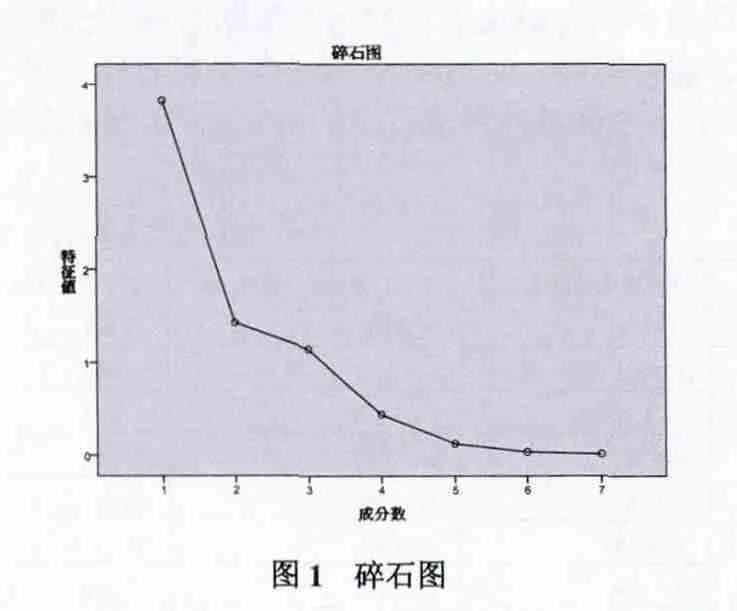
（3）主成分的矩阵表示

把工业废水排放量、工业废气排放量、工业氮氧化物排放量、工业烟粉尘排放量看作第一主成分，取名工业污染重要排放物；工业废水中化学需氧量排放量、工业二氧化硫排放量看作第二主成分，取名第二排放污染；工业废水中氨氮排放量看作第三主成分见表4。

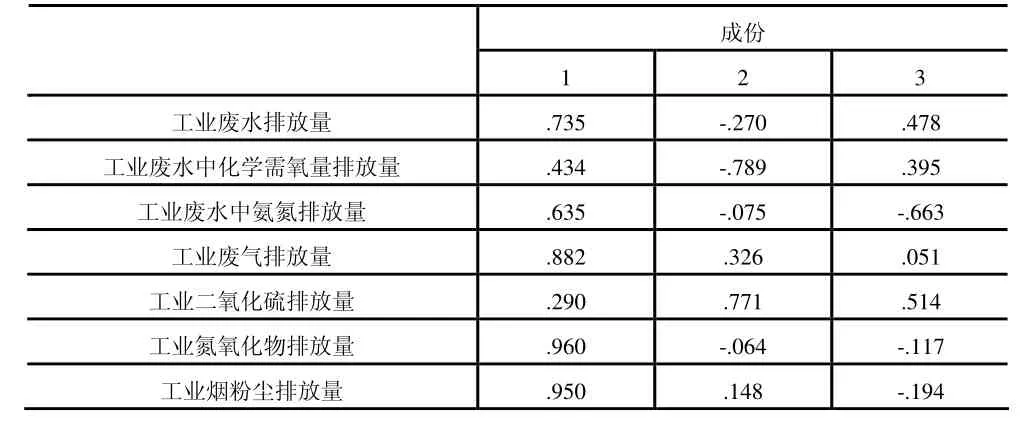
表4 原指标变量用主成分表示成份矩阵

（4）主成分的得分

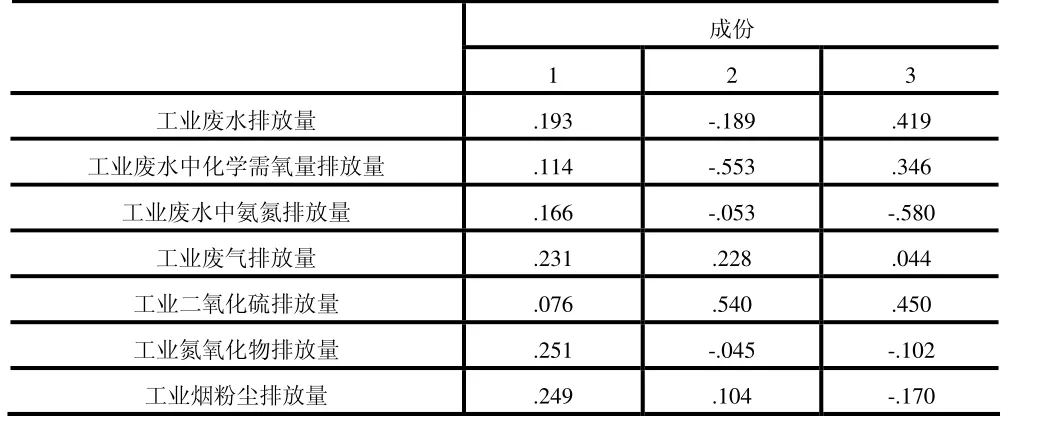
图5 主成分得分系数矩阵

则主成分的组合模型公式如下：

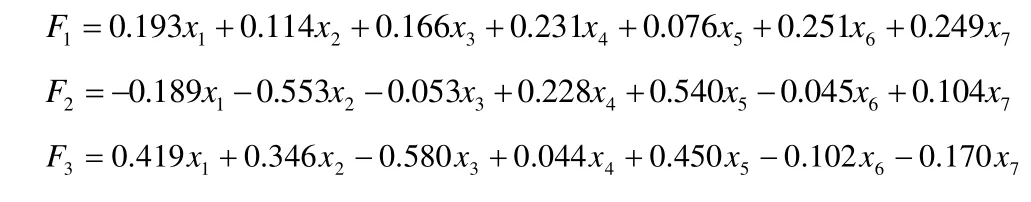
综合评价指数= 0.55 F1+0.2F2+0.16F3

可以将新疆各个行业的工业废水排放量、工业废水中化学需氧量排放量、工业废水中氨氮排放量、工业废气排放量、工业二氧化硫排放量、工业氮氧化物排放量、工业烟粉尘排放量的截面数据分别带入模型的公式F1，F2，F3中，并计算综合评价指数，根据其得分大小排序，就可以知道哪一个行业对环境污染的影响最大。综合得分见表6。

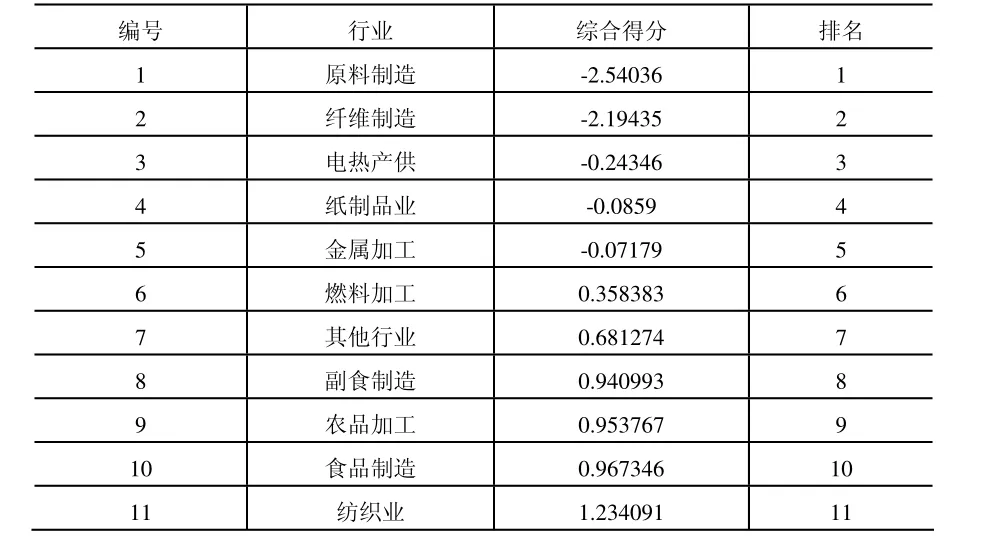
表6 各行业的综合得分

根据综合得分的表的排名，可知原料制造业的污染最大，纺织业的污染相对来说最小，所以更应该加强排名前三的原料制造业、纤维制造业、电热产供业的治理，这样才能使环境越来越好。

表7 主成分的协方差矩阵

1 1.000 .000 .000 2 .000 1.000 .000 3 .000 .000 1.000

根据表7可知，三个主成分两两之间的相关系数为0，说明经主成分分析提取后的三个主成分之间没有相关性，实现了主成分分析的优化设计目标。

2.2 聚类分析中的层次聚类

用R软件编程进行层次聚类分析，结果见图3。

根据图3可知将原料制造、纤维制造分为第一类，电热产供、纸制品业、金属加工、其他行业分为第二类，燃料加工、副食制造、农品加工、食品制造、纺织业分为第三类，采取大致的三类措施进行治理，这样不仅节约了资金也节省了时间。

3 小结

本文主要是用简单的统计方法得到了原料制造业、纤维制造业、电热产供业更需要加强对行业的管理，虽然其他行业综合得分不是很高，但是也不能松懈管理。文章的方法也可以应用到各个省市地区的各个行业，应用具有一定的广泛性。

[1] 李波,肖欢.1991～2011年甘肃省经济增长环境污染研究[J].现代商贸工业,2013(19):51-53.

[2] 王家庭.我国区域城市化与环境污染关系的空间计量研究[J].文明和谐与共同繁荣,2013:383.

[3] 闫丽霞.河南省产业结构升级与环境污染关系研究[J].低碳经济,2013(8):26-29.

[4] 新疆维吾尔自治区统计局.2013年新疆统计年鉴[M].中国统计出版社,2013.

[5] Richard A. Johnson,Dean W. Wichern. 实用多元统计分析(第四版)[M].清华大学出版社,2001.