基于机器视觉的液晶显示屏装配尺寸检测算法的研究

肖 敏 庄春刚 熊振华

上海交通大学，上海，200240

0 引言

液晶显示屏作为数码产品的重要部件，质量控制越来越严格［1］。实际应用中，为保护液晶显示屏，常使用塑料外壳进行固定。因此，液晶显示区域和外壳之间的距离是衡量液晶显示器质量的重要标准之一。由于液晶显示屏的产量大，清洁度和尺寸检测精度要求高，而采用人工检测存在检测速度慢、精度低、检测结果受检测人员主观影响较大、误检率和漏检率高等缺点［2］，因此采用视觉检测技术对装配好的液晶显示屏进行在线检测具有极大的优越性。将机器视觉引入到工业检测中，实现对产品尺寸或位置的快速测量，具有非接触、速度快、柔性好等突出优点，在现代制造业中有着广阔的应用前景［3］。

针对液晶显示屏显示区域和外壳之间距离这一装配尺寸的检测需求，我们开发了相应的检测设备和图像处理算法，对液晶显示屏进行实时在线的高精度检测。系统操作简便可靠，测量精度高，重复精度好，已经成功用于企业生产线上。

1 直线边缘检测算法及其实现

采用Point Grey公司的CMLN－13S2M型相机（分辨率为1280像素×960像素）和Computer公司生产的M2514－MP镜头，运动控制系统能精确控制相机和镜头运动到待检测区域。系统配置完全能够满足组装元件的检测精度要求。

对液晶显示区域和外壳之间的距离进行检测，其实质是对获取图像进行直线边缘检测并计算检测到的相关平行直线的距离。直线边缘检测算法主要有霍夫变换算法、最小二乘线性拟合算法［4］。

1.1 霍夫变换算法

霍夫变换利用点－线的对偶性，对图像进行某种形式的坐标变换，将原始图像中给定形状的曲线变换成空间中的一个点，从而使检测整体特性变成检测局部特性，使问题简化。

设在原始图像空间的直线方程为

将式（1）转换为极坐标，即

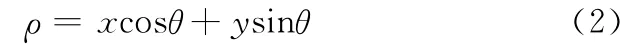
式中，ρ为原点到直线的距离；θ为该直线与极轴的夹角。

这样原始图像空间中的点在极坐标中表示的是一条正弦曲线，那么原始图像空间中的一条直线上的所有点对应着变换空间的一个曲线族，如图1、图2所示，点（ρ0，θ0）为变换空间中曲线族的交点（对应着原始图像空间中的直线）。所以，只要找到这个曲线族的交点就可以检测出直线。

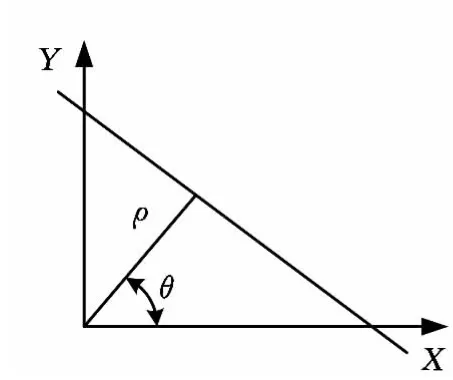
图1 直角坐标系下的直线

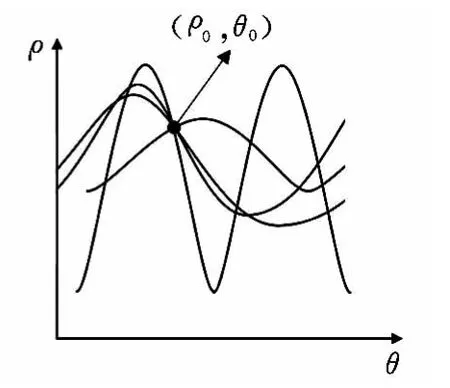
图2 参数空间下的曲线族

1.2 最小二乘线性拟合算法

图像的边缘共有n个像素，记作

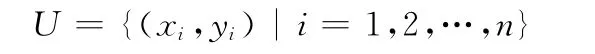
假设y与x的统计关系符合一元线性的正误差分布，对于给定的xi有如下的线性关系：

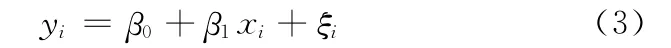
其中，β0、β1为直线方程的参数，ξi为点i对应的误差，假设其线性估计方程为

残差

残差的平方和为

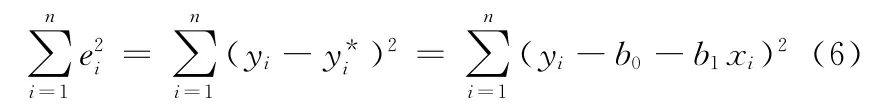
最小二乘线性拟合算法的思想就是找出参数b0、b1使式（6）最小，对式（6）求b0、b1的偏导，整理后便得到b0、b1的解［5］：

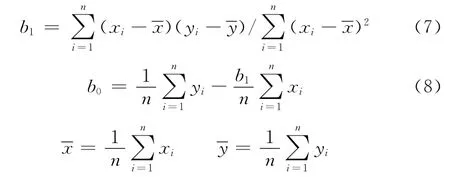
当x－y的关系满足假设条件时，y＊＝b1x＋b0是图像边缘的无偏拟合。但是当假设条件不成立时，如方程中存在系统误差，线性拟合精度不能得到有效的控制，会导致线性拟合误差偏大。

2 基于霍夫变换和最小二乘法的直线检测

霍夫变换算法是全局最优的直线检测算法［6］，具有较强的抗干扰能力，能很好地抑制噪声。但像差使直线在像面上可能发生不同程度的弯曲，此时用霍夫变换算法检测直线就不能得到准确的结果。相比而言，最小二乘线性拟合算法考虑了随机误差对线性检测的影响，其拟合直线是样本空间具有最小误差的无偏估计量，但最小二乘线性拟合算法假设误差服从正态分布，因此当边缘存在破损或毛刺等非随机误差时，拟合精度受到严重影响［7］。

为了保证液晶和塑料外壳直线边缘检测精度，我们使用霍夫变换和最小二乘法相结合的直线检测算法。该算法充分利用了霍夫变换较强抗干扰能力和最小二乘法拟合精度高的优点，满足了直线边缘在线检测要求，并在此基础上计算液晶显示区域和外壳直线边缘的距离。检测算法流程如图3所示。

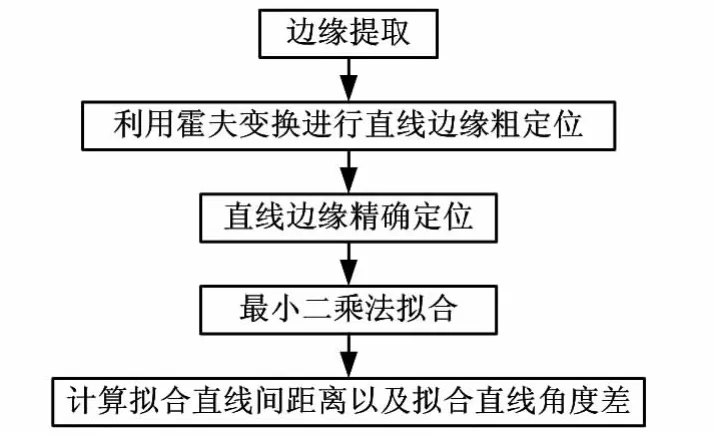
图3 检测算法流程图

2.1 边缘提取

为了保证检测的效率和精度，采用Canny算子进行边缘提取。图4为检测过程中相机拍到的实时图像，图5为使用Canny算子提取得到的边缘图像。

图4 相机拍到的实时图像

2.2 利用霍夫变换进行直线边缘粗定位

对使用Canny算子提取得到的边缘图像进行霍夫变换，并寻找霍夫变换矩阵的峰值。对于上述所得到的边缘图像，可以找到霍夫变换矩阵的6个峰值。

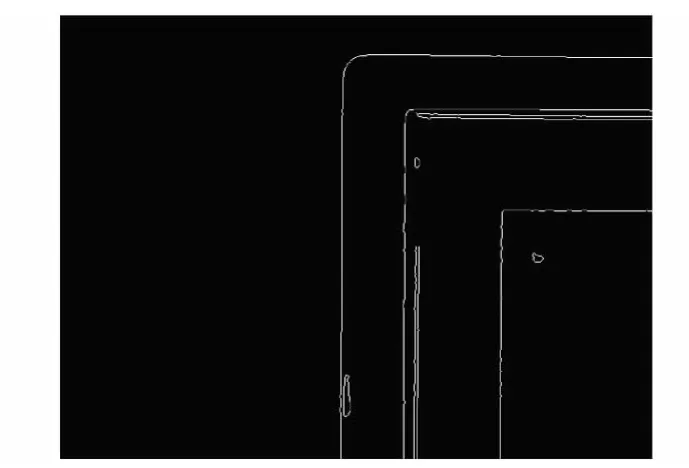
图5 Canny算子提取得到的边缘图像

由于直线在像面上可能发生不同程度的弯曲，所以图5中提取的边缘不是理想的直线，而用霍夫变换检测到的直线边缘只是原图中直线边缘的一部分，如图6所示。因此，霍夫变换对直线边缘的定位只是初步粗定位，并不精确。

图6 利用霍夫变换进行直线边缘粗定位结果

利用霍夫变换检测出的直线中，两条直线与极轴夹角的差值在±0.5°范围内时，被认为是在原图像中相互平行的直线。在图4中可以检测出2组平行直线。由于要测量的是液晶显示区域和塑料外壳之间的距离，即对应同组直线中Δρ最大的两条直线。根据θ和Δρ可以找到对应液晶显示区域和塑料外壳的直线边缘所对应的点（ρm，θm），m ＝1，2，3，4。

2.3 直线边缘精确定位

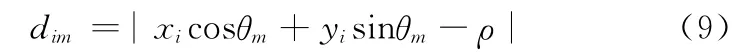
如果dim小于阈值d，则Vi（xi，yi）⊂，我们在检测过程中设置d＝2。采用上述方法精确定位到的直线边缘如图7所示。

2.4 最小二乘法拟合

对精确定位的各直线边缘上的点分别进行最小二乘法线性拟合，即可得到精确斜率km和截距bm。

2.5 计算距离以及拟合直线角度差

平行直线y＝kx＋b1和y＝kx＋b2之间距离为

图7 直线边缘精确定位结果

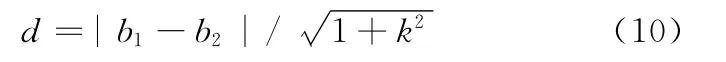
塑料外壳在安装过程中存在位置误差，边缘算法提取出的塑料外壳和液晶显示区域的边缘也存在误差，于是霍夫变换和最小二乘法得到的2条水平线和2条竖直线斜率各自存在微小差异。图7中，2条水平线经最小二乘法拟合得到的斜率：k1＝0.008和k2＝0.014，对应直线倾斜角相差0.1934°。因此拟合得到的2条水平线并不平行，如果使用式（10），无论使用k1还是k2，计算出来的距离都会有比较大的误差。

由于以上原因，在计算液晶显示区域和塑料外壳之间距离时，并没有直接使用平行直线的距离计算公式，而是根据两条拟合直线近似平行的特点设计了以下算法：

令W1和W2分别代表包含液晶显示区域和塑料外壳的图像经过直线边缘精确定位出来的一对直线上的所有点，W1拟合出的直线为y＝k1x＋b1，W2拟合出的直线为y＝k2x＋b2。计算W1中所有点到y＝k2x＋b2距离的平均值d1；计算W2中所有点到y＝k1x＋b1距离的平均值d2；液晶显示区域和塑料外壳之间距离d12＝（d1＋d2）／2。

拟合直线角度差

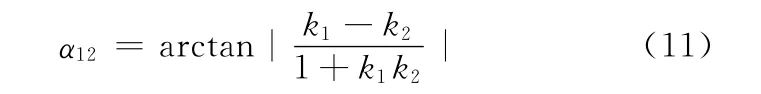
这一算法更符合统计学原理，计算得到的液晶显示区域和塑料外壳之间的距离也比直接利用平行直线之间距离公式得到的结果准确。

对于图4所示的照片，可以检测到2组平行直线边缘，进而可以算出2组直线边缘的间距d12、d34及对应拟合直线角度差α12、α34。其中，d12、d34为所检测的液晶显示区域和塑料外壳直线边缘的距离。

3 实验结果与分析

3.1 理想平行直线边缘检测

用计算机产生含有理想平行直线边缘的灰度图（已知距离）［8］，图像尺寸为500像素×500像素，如图8所示。

图8 理想平行直线边缘

现采用霍夫变换和最小二乘法相结合的检测算法与直接使用霍夫变换分别计算出的直线距离，如表1所示。实验中所产生理想直线的截距b1＝50，b2＝100，其倾斜角α1、α2见表1。

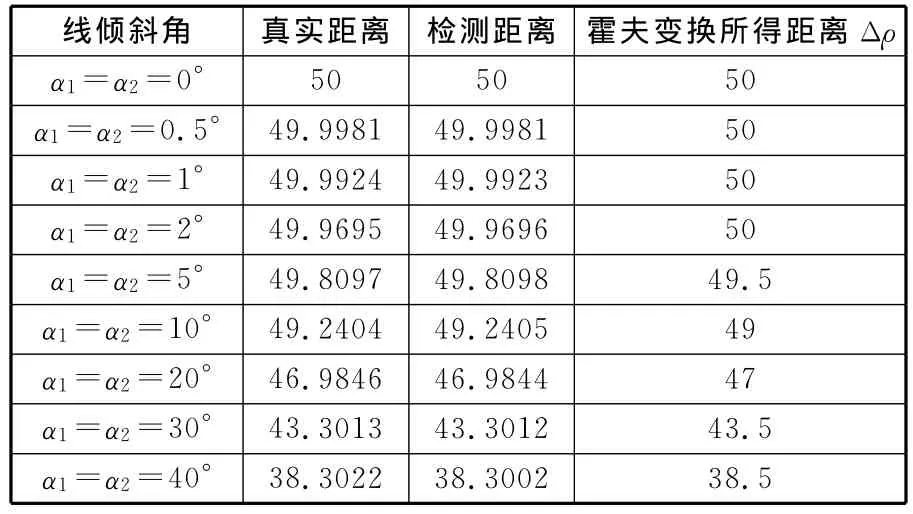
表1 检测已知距离平行直线实验结果 像素

从表1数据可以算出，直接使用霍夫变换检测理想直线边缘的平均误差是0.1113像素，而使用霍夫变换和最小二乘法相结合的直线检测算法检测理想直线边缘的平均误差是0.0003像素，检测精度显著高于霍夫变换的结果。在算法执行时间上，直接使用霍夫变换的方法平均时间为70.4ms，采用霍夫变换和最小二乘法相结合的检测算法平均时间为76.6ms。从该实验中可以看出提出的检测方法准确而且快速。

3.2 液晶显示屏装配尺寸检测

分别使用该视觉检测系统和镭射机，对液晶显示屏4个角的位置分别进行安装尺寸的实际检测，每一个位置检测10次后计算出平均值。检测结果如表2所示。

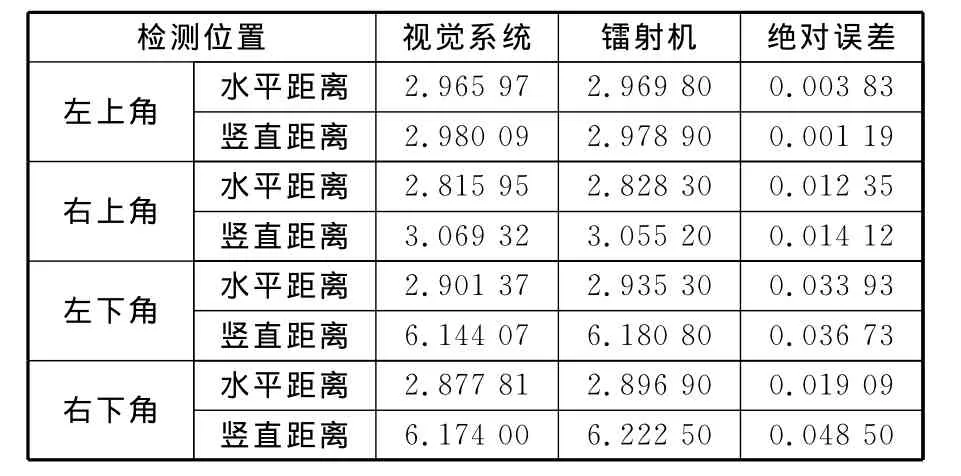
表2 视觉系统和镭射机的检测结果比较 mm

由于镭射机测量结果非常精确，因此将镭射机的测量结果当做液晶显示屏与外壳之间实际距离的参考值。从表2可以看出，使用该算法的视觉检测系统得到的液晶显示屏和外壳之间的尺寸和用镭射机检测到尺寸的绝对误差小于0.1mm。

4 结语

本文在比较分析常用直线边缘检测算法的基础上，提出了一种霍夫变换和最小二乘法相结合的直线检测算法，有效检测出液晶显示区域和外壳的直线边缘，并计算出拟合直线间距离和角度差。实验结果表明，提出的检测方法快速、高效、准确，该算法已经成功应用于液晶显示屏装配尺寸的在线检测。由于直线边缘检测使用非常广泛，因此文中提出的检测方法也适用于其他高精度直线边缘检测的应用场合。

［1］朱铮涛，姚钦，任涵文.基于图像处理的液晶保护屏玻璃板在线尺寸检测［J］.组合机床与自动化加工技术，2010（3）：55－58.Zhu Zhengtao，Yao Qin，Ren Hanwen.Realtime Dimensional Inspection of LED Protection Screen Based on Image Processing［J］.Modular Machine Tool ＆ Automatic Manufacturing Technique，2010（3）：55－58.

［2］伍济钢，宾鸿赞.机器视觉的薄片零件尺寸检测系统［J］.光学精密工程，2007，15（1）：124－129.Wu Jigang，Bin Hongzan.Dimensional Inspection System of Thin Sheet Parts Based on Machine Vision［J］.Optics and Precision Engineering，2007，15（1）：124－129.

［3］张舞杰，李迪，叶峰.基于视觉的贴片元件检测算法［J］.华南理工大学学报（自然科学版），2010，38（1）：65－69.Zhang Wujie，Li Di，Ye Feng.Vision Based Inspection Algorithm for Chip Components［J］.Journal of South China University of Technology，2010，38（1）：65－69.

［4］袁继栋，杨波，郑煜，等.高精度直线检测算法研究和误差分析［J］.现代制造工程，2011（2）：19－23.Yuan Jidong，Yang Bo，Zheng Yu，et al.Research on High Precision Line Detection Method and Error Analysis［J］.Modern Manufacturing Engineering，2011（2）：19－23.

［5］崔彦平，葛杏卫，张洪亮.机械零件直线边缘亚像素定位方法研究［J］.半导体光电，2010，31（5）：797－800.Cui Yanping，Ge Xinwei，Zhang Hongliang.Study on Beeline Edge Subpixel Localization for Mechanical Part［J］.Semiconductor Optoelectronics，2010，31（5）：797－800.

［6］周云燕，杨坤涛.基于RHT－LSM直线检测方法的研究［J］.光电工程，2007，34（1）：55－58.Zhou Yunyang，Yang Kuntao.Method for Line Detection Based on RHT－LSM［J］.Opto－Electronic Engineering，2007，34（1）：55－58.

［7］司永胜，姜国权，刘刚，等.基于最小二乘法的早期作物行中心线检测方法［J］.农业机械学报，2011，41（7）：163－167.Si Yongsheng，Jiang Guoquan，Liu Gang，et al.Early Stage Crop Rows Detection Based on Least Square Method［J］.Transactions of the Chinese Society for Agricultural Machinary，2011，41（7）：163－167.

［8］贺忠海，王宝光，廖怡白.理想边缘产生方法的研究［J］.光学精密工程，2002，10（1）：89－93.He Zhonghai，Wang Baoguang，Liao Yibai.Study of Method for Generating Idea Edges［J］.Optics and Precision Engineering，2002，10（1）：89－93.