三种非线性趋势项的提取方法在生物医学信号分析中的应用

【作 者】王步青，张政波，王卫东

解放军总医院医学工程保障中心，北京市，100853

0 引言

趋势分析（Trend Analysis）一般意义上的定义是：一种时间序列的分析方法，用来估算和研究某一时间序列在长期变动过程中存在的规律性。通常采用的是基于加权滑动平均法和基于拟合曲线的方法来获得数据中的趋势。这两种方法均是对观测信号进行了如下的假设：即信号由趋势项数据和随机加性噪声合成。前种方法通过集总平均去掉噪声得到趋势信号，第二种方法通过先验知识获得趋势信息，采用特定的函数或多项式对数据拟合来获得趋势信号。然而，由于在生物医学信号处理中，实际生理信号均为非线性、非平稳，且非先验，以上这些方法不适用。

生物医学信号包括直接从生物体采集到的心电信号、脉搏波信号、呼吸信号等，也包括从以上基本的信号通过提取特征点后构建的新信号，例如从心电信号获得的R-R间期序列（心率变异性，HRV），心电和其对应的脉搏波特征点间期构成的脉搏波传导时间序列（PTT）等。它们均为非平稳随机信号，根据不同的研究目的，需要将非平稳序列中的趋势序列和非趋势序列进行分离。一方面可以获得信号的趋势信息，有利于掌握在长期变动过程中信号中存在的规律性；另一方面可以对非趋势信号（平稳随机信号）进行时间与频率尺度上的能量分布的相关研究，以便从中提取出可用于疾病诊断的特征信息。本文主要介绍针对具有非平稳随机性的生物医学信号的分离非线性趋势序列的3种方法：小波分析法、经验模式分析法和平滑先验法。在介绍基本原理的基础上，将其分别应用于三种不同的生物医学信号的非线性趋势成分的分离和分析中。

1 三种非线性去趋势方法

1.1 小波分析法

小波方法[1]具有良好的局部化特性和处理突变信号的能力，可应用于非线性趋势的分析中。所谓小波变换就是选择适当的基本小波(母小波)，通过对基本小波平移、伸缩而形成一系列的小波，然后将欲分析的信号投影到由平移、伸缩小波构成的信号空间中。式(1)为小波变换表达式，其中平移参数b的变化决定时窗的位置，而尺度参数a的变化不但改变连续小波变换的频谱结构，同时也改变了窗口的大小和形状。当小波变换的平移因子和尺度因子为离散情况时称为离散小波变换。

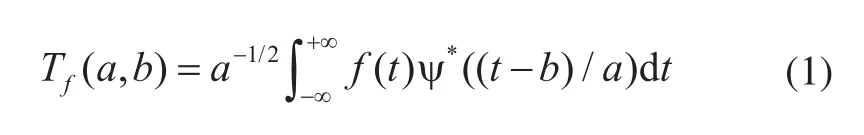
ψ(t)为母小波，* 表示复数共轭运算

由于信号的小波变换相当于小波分解在不同尺度的带通滤波信号，而小波分解逼近信号为各尺度下的低通滤波信号，在尺度为N的分解波形中可以看到，信号中的直流分量及趋势项明显地显现在N尺度的逼近信号上，因此只要在小波变换重构的过程中,将该尺度下的分量置零，就可以得到去除了直流及缓变趋势分量的重构信号。

1.2 经验模式分解法

经验模式分解（Empirical Mode Decomposition，EMD）[2]是Norden.E.Huan 在1998 年提出的一种适用于非平稳、非线性信号的处理方法，它将复杂（包括平稳与非平稳，周期与非周期）时间序列分解成为获得一系列表征信号特征时间尺度的本征模函数（Intrinsic Mode Function，IMF），使得各个IMF 是窄带信号。由此，EMD 方法的本质就是将信号分解为若干个IMF 之和，不同的IMF 具有不同的尺度特征，从而有利于我们对信号进行更为细致的分析。在某些实际应用中可以根据不同需要，把某些IMF 进行适当组合，便可构成高通、低通、带通滤波器，实现生物医学信号滤波、频带分离和降噪。针对EMD存在的模态混叠(Mode Missing)等问题，Huang 等人在2009年进一步发展出了EEMD （Ensemble Empirical Mode Decomposition,EEMD）的信号分解方法。EEMD以噪声辅助信号处理为基础，通过加入小幅度的白噪声来均衡信号，利用高斯白噪声零均值的特性，使真实信号得到了保留，在一定程度上解决了模态混叠问题。

1.3 平滑先验法

平滑先验法原理(Smoothness Priors Approach，SPA)[3]是芬兰库奥皮奥大学的Karjalainen博士最先提出的一种信号非线性去趋势方法。假设原始序列Z包含两部分：

式中：Zstat为信号z中的平稳项；Ztrend为非线性趋势项。其中

式中：

H∈RN×M为观测矩阵，N为数据长度，θ∈RM为回归参数，v是观测误差，通过正则化最小二乘法准则估计参数θ，得到趋势项的最优估计为：

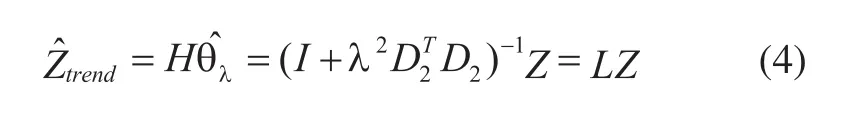
式中，I∈RN×N，D2∈R(N-2)×N为二阶微分矩阵，相当于一个离散时间序列的高通滤波器。在确定参数后可以利用式（4）得到趋势项。

2 三种方法的应用举例

2.1 小波分析法应用于心电信号的去基线

心电信号基线漂移的表现形式为在信号上叠加了一个低频慢变趋势项，这样会使采集到的原始信号的波形发生较大的变化，是噪声干扰的主要来源之一，往往对于信号的播放、识别和分析造成一定的影响。通过小波分解，将低频的逼近信号去掉后，可以得到去基线的信号。如图1(a)上的黑色波形为原始心电信号，淡灰色波形为使用db6小波对其心电进行8层分解，得到的低频逼近信号a6，图1(b)为将低频逼近信号a6置0后，重构得到去基线的ECG波形。

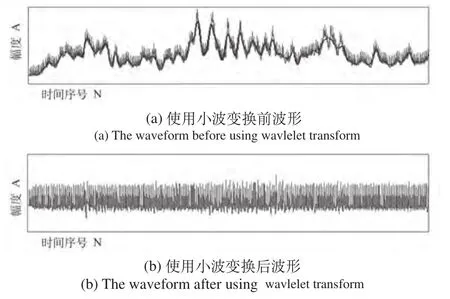
图1 使用小波变换去心电基线趋势前后的波形Fig.1 The waveform before and after detrending using wavelet transform

2.2 经验模式分解法应用于脉搏波传导时间信号的趋势提取

脉搏波传导时间(Pulse Transit Time,PTT)是动脉血压波沿血管壁的传输时间，它的计算通常是ECG的R波峰与相应心动周期的PPG信号起点间的时间间隔。脉搏波传导时间和平均动脉压有很强的相关性。因此通过研究PTT信号，就可以得到血压、外周阻力的相关变化信息。

图2为一引导呼吸下的PTT随呼吸调制的变化曲线，呼吸引起胸内压的改变，从而引起PTT相应变化，而PTT基线则代表了呼吸的作用累积的效果，PTT基线上升则表明系统血压或者外周循环阻力降低。为有效分解出PTT基线和PTT幅度变化两个成份，对于经过EMD分解出的14个IMF，将低频慢变成分IMF 10-14合并，作为PTT基线成分（即趋势成分）即图2中的深色曲线。

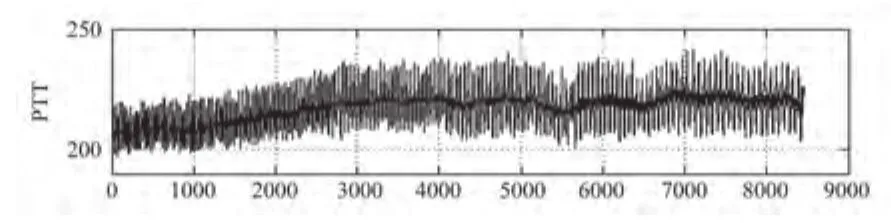
图2 基于EMD的PTT信号分解Fig.2 The decomposition of PTT based on EMD

2.3 先验平滑法用于心率变异性的去趋势分析

由于心率变异性（R-R间期序列）已被普遍认为是混沌的或是含有混沌成分的非线性、非平稳信号，因此在进行基于平稳随机序列的AR模型的功率谱分析之前应先进行去低频的趋势处理，将非平稳随机信号变成平稳随机信号。这里采用先验平滑法用于去趋势。根据对原始的R-R序列进行4 Hz的重采样处理后，得到原始HRV信号的关于L的时变频率响应，如图3所示，在N的中点时刻不同参数下频率响应曲线如图4所示，在选择λ为300时可以实现截止频率为0.04 Hz以下的趋势项的去除。

图3 HRV信号的关于L的时变频率响应Fig.3 The time varing frequency response of HRV based on L

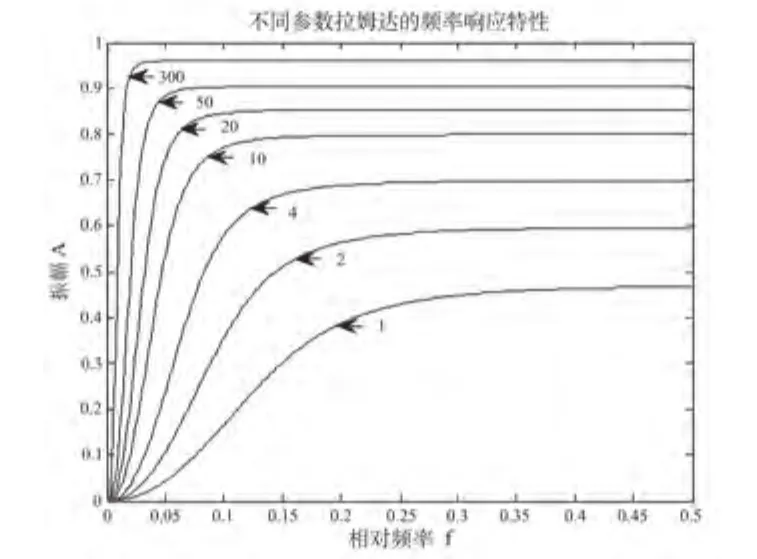
图4 不同参数下频率响应曲线Fig.4 The frequency response curve based on different parameter

图5的浅色波形为原始含有趋势项的HRV信号，其中深色波形曲线为使用先验平滑法得到的趋势曲线。

3 讨论

图5 使用λ=300的平滑先验法对HRV去趋势Fig.5 The detrending of HRV using smoothing prior method when lambda equals to 300

小波分析法是采用特定的小波基来分解非线性、非平稳信号。但因其计算结果与小波基的选择密切相关，限制了它的实际应用，特别是在定量分析中。它常用于预处理的信号降噪中。

经验模式分解法(EMD)是利用不断重复的筛选程序(Sifting Process)将非平稳、非线性信号分解成多个本征模态函数(IMF)。它是无需任何先验知识的自适应分解法，其分解基依赖于信号本身的特征，因此经验模式分解法比小波分析法具有更强的适应性，对于分析弱噪声背景下的缓变信号是可行的。但是在信噪比低的强噪声干扰下，会使EMD分解出来的IMF产生畸变。在这种情况下，需要将两种方法结合起来使用，先利用小波分析法去除噪声干扰，然后使用EMD法去趋势。

小波分析法在非线性趋势成分的应用中，主要取决于选择何种小波基来进行小波分解以及小波分解的层数；EMD进行非线性趋势分析主要取决于选择多少个低频的IMF之和作为趋势项，而以上的这些参数的具体选择大多是根据实际的经验来定的。

先验平滑法是一种基于正则化原则的去非线性趋势的方法。此方法不同与前面的两种经验分析法，在这种方法中趋势项的截止频率与特征参数的存在着一一对应的数值关系。因此在实际计算中，可根据计算需要，得到对应频率成分的趋势项。且由于计算简单，可用于实时的计算中。

4 小结

传统的时间序列的趋势分析多基于一定的统计特性，研究时间序列在长期变动过程中所存在的统计规律性。本文主要针对生物医学信号分析中的3种去非线性趋势方法进行了原理的介绍，这些方法可根据不同的分析目的和不同的信号特征，应用于各类生物医学信号处理中的趋势提取、滤波、非平稳序列平稳化等应用中。

[1]彭玉华.小波变换与工程应用[M].北京: 科学出版社,2002.

[2]Huang NE,Shen Z,Long SR,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis[J].Proc R Soc Lond A,1998,454(1971): 903-993.

[3]Karjalainen P.Regularization and Bayesian methods for evoked potential esimation[D].University of Kuopio,Department of Applied Physics,1997.