基于遗传算法的舰船抗沉决策模型研究

胡丽芬，鲁 江，毕俊颖，张克正

(1.鲁东大学 交通学院，山东 烟台264025;2.中国船舶科学研究中心，江苏 无锡214082)

0 引 言

安全是现代海战的重要因素之一。虽然舰船安全受很多不可控因素的影响，但是有效的舰载监测系统能将危害降到最低。随着船舶设备复杂程度的不断提高，尤其是现代舰船，因其有复杂的舱室布置和武器设备，对舰船抗沉指挥提出了更高的要求。因此舰船一旦破损，需要决策者及时了解和掌握舰船的基本状况，并迅速制定出正确有效的抗沉决策方案。迄今为止，还没有一个确定的准则来评估抗沉方案的优劣，因此本文提出一种抗沉决策模型，并引入遗传算法来求解［1］。

作为一种经典的优化方法，遗传算法被广泛应用于工程设计领域求解约束优化问题［2-3］。近年来的研究重点集中在紧急情况下抗沉方案的生成，但是对于抗沉方案的好坏还没有一个确定的评估准则。本文将抗沉决策优化模型转化为单目标规划问题求解，辅助指挥员紧急情况下快速决策。

1 抗沉决策模型

1.1 目标函数

一般来讲，最优抗沉方案应能保证横倾和纵倾最小，而干舷较大，如果作为多目标规划问题处理，各指标之间的权重很难分配［4］。本文将其作为一个单目标问题处理，因倾斜角同时考虑了横倾和纵倾，采用倾斜角作为目标函数来评估抗沉方案。之前的研究考虑最小干舷作为目标函数［5］，但是需要计算各横剖面的干舷值，然后找出其中最小值，因此耗时多。相比干舷计算，倾斜角更易计算。因此，本文提出倾斜角作为目标函数:

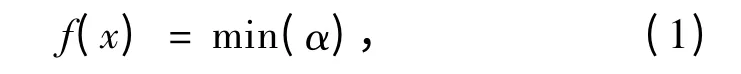
根据船舶不沉性理论［6］，倾斜角的计算公式如下:

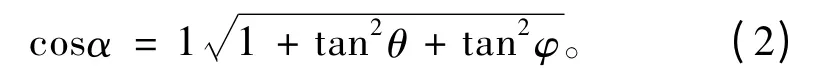
其中，α 为倾斜角，(°);θ 为横倾角，(°);φ 为纵倾角，(°)。该值越小，船舶的浮态越好。

1.2 设计变量

生成最优抗沉方案的关键是调整可用抗沉舱［7］，针对破损载况找到一个可行的方案，以便能有效扶正舰船。因此设计变量取各个可用抗沉舱的装载量。

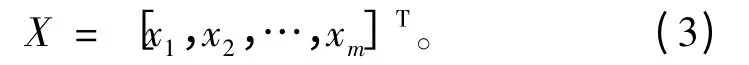
其中，x1，x2，…，xm为m 个抗沉舱的装载量，为避免自由液面对船舶稳性的不利影响，抗沉舱的装载非空即满。因此抗沉舱的装载状况:100%装载，空载，保持原有装载不变以及破损。

1.3 约束条件

由于已经破损的抗沉舱不能用来调整浮态，抗沉舱不破为一个约束条件。同时本文主要针对初稳性高为正时的抗沉方案，要求初稳性高GM ＞0。因此，可用抗沉舱的载况为:100%装载，空载，保持原有装载不变。约束条件如下:

2 遗传算法

遗传算法是一种基于种群的搜索算法，能有效避免局部收敛，用来解决搜索和优化问题。它基于生物进化仿生学算法，是一种智能化、自适应概率性全局优化搜索算法［8］。主要特点是群体搜索策略和群体中个体之间的信息交换，其搜索不依赖于问题的梯度信息，尤其适用于处理传统搜索方法难以解决的复杂和非线性问题。与传统的优化方法相比，它具有使用简单、全局寻优能力强等特点，是当今求解优化问题最有效的方法之一［9］。遗传算法开始于决策问题的一组初始解，即初始种群，每个解决方案称为染色体，交叉和变异用来生成下一代种群直到满足停止准则。

遗传算法的有效性和可行性已在实际应用中被证实，然而，对于一个具体的优化问题，使用者必须合理确定遗传算子、算法参数以及约束的处理方法，它们会对优化结果产生直接影响。本文提出的遗传算法如图1所示。

2.1 染色体

遗传算法不能直接处理工程实际问题空间的参数，必须把它们转换成遗传空间由基因按一定排列组成的染色体。对应不同的工程问题，编码方法也不一样。本文采用符号编码法，分别由“0”，“1”，“2”，“3”组成。遗传算法中的染色体即优化设计中的设计变量，染色体上的每一位即每一个设计变量称为基因。x1，x2，…，xm表示m 个设计变量，m 为染色体长度。例如:“00012332121110002222”表示一组解，解码之后每个基因值表示每个抗沉舱的装载量。初始种群用随机方法产生。染色体长度即设计变量维数，取为25。

2.2 解码

基因“0”表示抗沉舱为空，舱室的容积和重心为0;基因“1”表示抗沉舱为满，舱室的容积和重心直接从舱容表中读出;基因“2”表示抗沉舱保持原有容积不变，舱室的容积和重心不变;基因“3”表示抗沉舱破损，舱室的容积和重心为0。

2.3 适应度计算

一般地，适应度函数是由目标函数按一定的规则转换而来。本文建立的适应度函数如公式(5)所示:

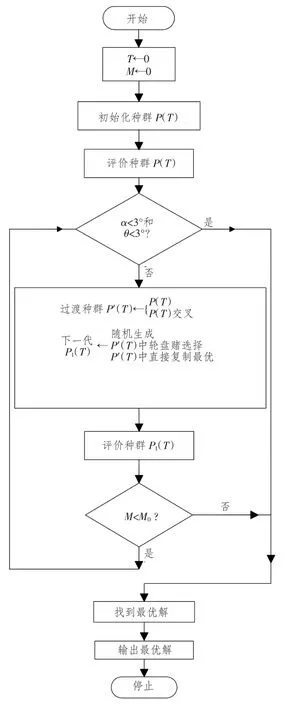
图1 遗传算法计算流程Fig.1 The process of genetic algorithm

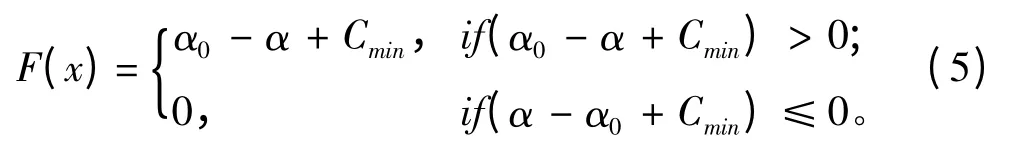
其中，α0为破损舰船的倾斜角;α 为生成的抗沉方案对应的倾斜角;Cmin为一个相对小的数。通过转换，种群既保持了多样性，又淘汰了差的个体。

2.4 选择过程和交叉算子

在图1 的流程中，交叉函数从当前种群P(T)中选择N 个个体进行单点交叉操作，得到过渡种群P′(T)，P′(T)是个扩大的种群空间，由N个个体和随机生成的n 个个体组成。此处，n=0.5N，下一代种群P1(T)组成:85%N 采用轮盘赌方法从P′(T)中选择，染色体被选中的概率和它的适应值成正比;5%N 直接从P′(T)复制最优的;10%N 为随机生成新的个体。轮盘赌方法的步骤如下:

4)产生一个［0，1］区间的随机数r;

5)如果r ＜q1，则选择X1，否则选择Xj(2≤j ≤N);

6)重复步骤4和步骤5 共l 次，得到l 个染色体。

2.5 复制和变异

直接复制当前最优个体的进化策略倾向于收敛到局部最优。通过在扩大的种群空间上进行变异和选择操作，即使交叉和变异率很高，进化过程中也不会产生太多的随机波动。变异操作是在下一代引入一些新的个体，新个体由随机向量初始化产生，并非传统的基因对基因的变异(每一代的变异概率很小)，同时也避免收敛到局部最优解。

2.6 停止准则

如果找到最优解，或者满足给定的计算时间，程序迭代计算停止。本文采用倾斜角和横倾角作为停止准则，更容易限制横倾和纵倾。满足停止准则即可输出最优解，能明显减小计算时间。同时为了避免程序溢出，进化代数M0为另一停止准则，如果倾斜角不能满足给定要求，只要进化代数超过给定的最大进化代数，程序就输出当前的最优解。

3 实例分析

为了验证本文所述的优化方法和优化模型的有效性，以某船为例，基于Visual- Basic 6.0 语言，编制了相应的计算程序，并采用遗传算法进行了计算。该船的主要尺度为:Lpp=114 m，D=8 m，B=12 m，T=4.5 m。破损前载况接近标准排水量，破损状态为中后部右舷破损。

表1 遗传算法的基本要素Tab.1 The elements of genetic algorithm

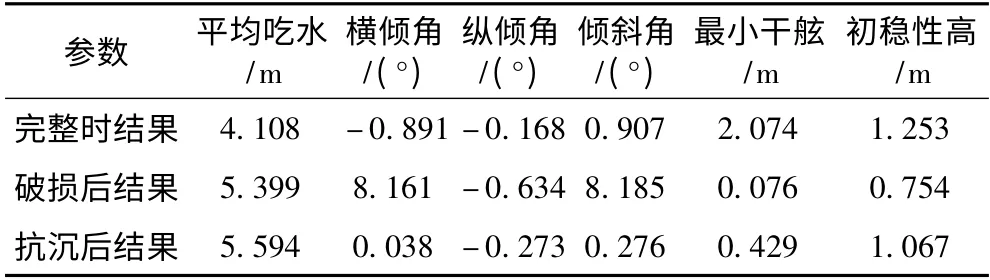
表2 完整和破损后的浮态和初稳性高计算结果Tab.2 The results of calculation

表1 中，种群大小为100，交叉概率为0.8，最大迭代代数为200 代。根据抗沉调整原则，为了用尽可能少的舱室获得最优的抗沉效果，如果是压载操作则优先选择远离破损区域的横向对侧舱室，如果是排空操作则优先选择离破损区域尽可能近的纵向同侧舱室。根据表2 中的计算结果，生成的抗沉方案实施后，横倾已经消除，稳性也满足不沉性的相关要求。同时，选择倾斜角作为目标函数能明显减小计算时间，进而证实了提出的优化模型和遗传算法的可行性。

4 结 语

1)本文以倾斜角为目标函数，可用抗沉舱为设计变量，建立了抗沉决策的优化模型，采用改进的遗传算法进行求解。

2)通过对某破损舰船进行抗沉调整的实例计算，证实了提出的优化模型的可行性及其求解算法的有效性。

3)结果表明:选择倾斜角为目标函数比最小干舷能明显减少计算时间，更适合在紧急情况下快速决策。

［1］玄光男，程润伟.遗传算法与工程优化［M］.北京:清华大学出版社，2004.

［2］CHEN Jing，LIN Yan，ZHOU Huo-jun，et al.Optimization of ship′ s subdivision arrangement for offshore sequential ballast water exchange using a non-dominated sorting genetic algorithm［J］.Ocean Engineering，2010，37:978-988.

［3］甘世红，吴燕翔，李军军，等.基于遗传算法的模糊控制型船舶自动驾驶仪研究［J］.中国造船，2011，52(1):173-179.

GAN Shi-hong，WU Yan-xiang，LI Jun-jun，et al.Investigation of fuzzy ship autopilot based on the genetic algorithm［J］.Shipbuilding of China，2011，52(1):173-179.

［4］DONGKON L.Knowledge-based system for safety control of damaged ship［J］.Knowledge-Based Systems，2006，19:187-191.

［5］HU Li-fen，MA Kun.Genetic algorithm-based counterflooding decision support system for damaged surface warship［J］.International Shipbuilding Progress，2008，55(4):301-315.

［6］马涅采夫.船舶不沉性理论［M］.北京:国防工业出版社，1977.

［7］HU Li-fen，MA Kun，JI Zhuo-shang.A M-H method-based decision support system for flooding emergencies onboard warship［J］.Oceaning Engineering，2013，58:192-200.

［8］李学斌.多目标遗传算法在船舶操纵性优化设计中的应用［J］.造船技术，2008，284(4):10-12.

LI Xue-bin.Multi-objective evolutionary algorithm in the optimal design of the detailed-design［J］.Marine Tochnology，2008，284(4):10-12.

［9］王福林，吴昌友，杨辉.用遗传算法求解约束优化问题时初始种群产生方法的探讨［J］.东北农业大学学报，2004，35(5):608-611.

WANG Fu-lin，WU Chang-you，YANG Hui.Study on the productive method on the initial population by using genetic algorithms to solve the constrained optimization problems［J］.Journal of Northeast Agricultural Vniversity，2004，35(5):608-611.