螺旋桨水动力性能及流固耦合数值模拟

黄 璐，陈 立，邱辽原，解学参

(中国舰船研究设计中心，湖北 武汉430064)

0 引 言

船用螺旋桨水动力性能数值预报的方法主要基于粘性流或势流。基于势流理论的升力线理论，升力面理论和面元法虽然广泛应用于螺旋桨的设计与性能预报，但由于势流理论忽略了流体粘性的影响，无法准确预报螺旋桨的尾流场。随着CFD 技术的发展，利用CFD 技术预报螺旋桨的水动力性能开始得到广泛的应用。目前粘性流的计算主要是基于RANS 方法，对螺旋桨周围流场进行数值预报与流场分析，计算结果与实验结果吻合较好。

常规的螺旋桨强度计算采用分析计算法，该方法把桨叶作为简单的悬臂梁，推力系数和扭矩系数沿桨叶径向的分布形式按经验公式来假定，假定线性规律分布，计算包含大量简化，因此这种方法不能准确的进行强度计算。有限元法是将连续的求解域离散为一组有限个单元的组合体，这样的组合体能解析地模拟或逼近求解区域。因此，采用有限元法可以准确的对螺旋桨结构强度计算，得到桨叶变形及产生的应力。

螺旋桨数值预报的影响因数有很多，如几何模型的精确度、网格类型和质量、湍流模型、离散方式、求解算法等。本文采用Gambit 软件，根据螺旋桨的投影原理及型值参数进行三维建模。基于结构/非结构网格分区拼接嵌套技术，分别进行分区混合流体网格和结构网格的划分，采用Fluent 软件对敞水螺旋桨的水动力性能进行数值模拟，并分析流场的一些重要现象及特征。根据流场计算结果，将螺旋桨敞水工作时的桨叶受力加载到有限元分析软件中分析螺旋桨的应力及变形，研究螺旋桨敞水时的单相流固耦合作用，校核桨叶的结构强度，并为后续螺旋桨流固耦合问题分析提供参考。

1 计算模型的建立

选取DTMB P4119 桨进行数值模拟，其几何参数如表1所示。

表1 DTMB P4119 螺旋桨的几何参数Tab.1 Geometric parameters of DTMB4119

螺旋桨建模时，首先将以型值表形式表达的螺旋桨叶切面的局部坐标转换为全局坐标，坐标转换公式为:

螺旋桨三维建模采用点、线、面、体的顺序依次完成。把桨叶各半径处型值点的空间坐标导入Gambit，用NURBS 命令生成桨叶周边曲线，根据周边曲线建立桨叶曲面，最终生成螺旋桨桨叶。将桨毂简化成中部圆柱体、两端椭球体，并用缝合命令将桨叶和桨毂缝合成一个实体。

图1 桨叶局部放大图Fig.1 Enlarged partial view of blade

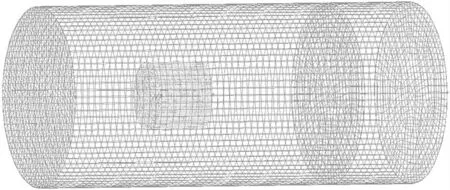
图2 螺旋桨及整个流域网格划分螺旋桨Fig.2 Mesh of the propeller and computational domain

2 网格划分及边界条件设置

2.1 流体网格划分

为了精确地获取螺旋桨围流场的信息，避免流场变化平缓区域的计算资源浪费，对整个计算域进行分区网格划分。基于不影响计算精度，亦不浪费计算资源的原则，取计算域为直径5D，长度12D 的圆柱体，此为静流域。同时，建立直径2D，长度1.5D 的小圆柱体作为动流域。对于动流域，采用非结构网格对桨叶与桨毂连接处以及叶梢进行局部加密，以便捕捉到重要的流场信息。对于静流域，采用结构网格适当降低密度。

2.2 结网格划分

由于流体计算和结构计算采用的是非同种单元类型，使用Gambit 软件对已有的螺旋桨虚体进行内部有限元网格划分。为保证求解精度和数据传递的准确性，在划分有限元网格时采用适应性好的三角形网格并利用尺寸函数对桨叶与桨毂连接处以及叶梢进行局部加密。

2.3 边界条件设置

进口边界条件设置为速度进口，给定相应进速系数下的速度。出口边界条件设置为压力出口。圆柱体的侧面设置为壁面边界条件，壁面为无滑移固壁条件。由于静流域和动流域的表面网格不一致，在Fluent 中无法传递计算，将交界面设置成interface 边界条件，从而面两边的不同的网格通过此面进行信息传递。动流域的运动形式为MRF，绕X 轴旋转。静流域与螺旋桨静止水中相同，仍为静止流体。

3 敞水计算结果与分析

3.1 敞水性能曲线计算结果与实验对比

螺旋桨旋转速度设置为10 rad/s，在设计进速系数J=0.833 左右两边分别取J=0.5，J=0.7，J=0.9，J=1.1 选取SST 湍流模型进行模拟，求得不同进速系数下的推力和扭矩，进而求得推力系数KT、转矩系数KQ 以及敞水效率。将计算值与实验值绘制成图，如图3所示。

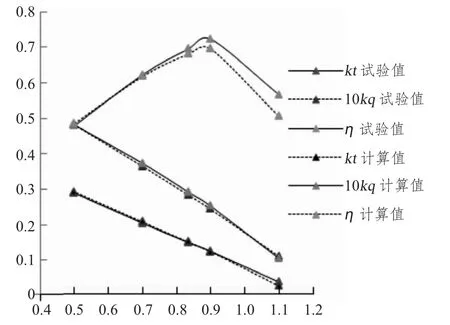
图3 螺旋桨敞水性能曲线Fig.3 Open-water performance curve of propeller

由敞水性能曲线可以看出，计算值与实验值吻合较好。除了J=1.1 处，计算所得的推力系数的平均相对误差为0.79%，转矩系数的平均相对误差为2.25%，敞水效率的平均相对误差为2.04%。J=1.1 时的误差原因是因为螺旋桨在相同转速和直径下，进速系数越大，来流速度越大，但相应的推力和扭矩越小，所以小干扰就会导致试验值和计算值之间很大的误差。另一可能原因是计算时并未考虑螺旋桨的空化模型，从而导致的误差。总的来说实验值与计算值吻合良好。

3.2 螺旋桨表面压力分布

通过螺旋桨的表面压力分布云图4，可以观测到螺旋桨的表面流场特性。螺旋桨压力在从随边到导边逐渐增大，并在导边处达到最大值。在某一固定进速系数下，叶面的压力从叶根到叶梢，不断增加，达到一定值后，然后逐渐减小，在叶梢处达到最小值。随进速系数的增加，叶面的导边和随边的高压区域开始收缩，叶面的压强变小。叶背的高压区从随边逐渐向导边扩张，使整个叶背区域的压力趋于平均，导边和随边相对较大，中间相当一部分压力较小。叶背总压由负值向正值变化，说明叶背的吸力能力越来越小，其“推力”作用越来越大。叶面与叶背之间的压力差逐渐变小，从而解释了螺旋桨的推力随进速系数的增加而变小的原因。叶面总体的变化不如叶背的变化大，从而说明进速的变化对叶面总压的影响不若叶背的影响大。

图4 螺旋桨桨叶压力分布图Fig.4 Pressure distribution of blade

图5 不同进速系数下螺旋桨尾流图Fig.5 Wake diagram of different advanced coefficients

3.3 螺旋桨尾流

如图5所示的J=0.5，J=0.833，J=1.1 时螺旋桨尾涡可见:外直径处尾涡螺距随J 的增大而上升，内直径处尾涡螺距随J 增大而下降。较大半径处的尾涡螺距随J 的增大而上升，较小半径处尾涡螺距随J 的增大而下降。这与文献［2］中采用PIV测量四叶侧斜桨尾涡揭示的规律相同。

4 螺旋桨流固耦合分析

本文的流固耦合问题中，利用支持耦合场分析的Workbench 软件，该软件在流固耦合功能中提出一种新 的 Immersed Solid流固耦合(Fluid－Solid Interaction，FSI)算法，该算法基于网格重叠技术，流体和固体区域各自拥有一套网格，可以支持模拟运动流场中运动刚体与流体的相互作用。在进行单向流固耦合计算时，基于CFX－Post，使得桨叶表面压力在Fluent和Mechanical 产品间进行单向载荷传递。

4.1 螺旋桨的材料及力学性能

螺旋桨材料选取高锰铝青铜合金，其牌号和力学性能如表2所示。

表2 高锰铝青铜合金材料特性Tab.2 Materials characteristicals of ZQAL 12－8－3－2

4.2 不同进速下桨叶表面应力与变形分布

以桨毂为固定面进行计算，得出的应力和变形计算结果分别如图6和图7所示。

图6 不同进速下桨叶表面应力分布Fig.6 Blade stress distribution of different advanced coefficients

图7 不同进速下桨叶表面变形分布Fig.7 Blade deformation distribution of different advanced coefficients

由图可知，桨叶应力集中在叶根弦向中部区域，且等高线从应力集中位置以类似同心椭圆状分布。桨叶的最大变形发生在叶梢部位，且变形量随直径的减小而减小。随着进速系数的增大，叶梢的最大变形从导边向随边处发生移动。最大变形发生在叶梢而不是在最大应力处的原因可能是叶梢厚度薄，该部位刚度较小，而且该处压力较大，易于发生变形。

4.3 桨叶最大应力变形分布分析

由图8 可以看出，低进速系数情况下的最大应力及最大变形比高进速系数情况下的最大应力及最大变形大。这是因为螺旋桨在高进速时为轻载状态，推力和扭矩较小;低进速时为重载状态，推力和扭矩较大。根据曲线，J 在0.5 ～0.9 时，最大应力和最大变形随进速系数增大呈线性递减规律。因此考虑建模、流体计算等误差在内，桨叶表面的最大变形和最大应力和进速系数之间存在线性关系。根据螺旋桨常用材料的性能和许用应力范围，取其安全系数约为10 左右。高锰铝青铜合金的抗拉强度为990 ～735 MPa，屈服强度为280 ～345 MPa，图中最大应力为3.72 MPa，远小于许用应力。

图8 螺旋桨最大应力及最大变形曲线图Fig.8 Maximum stress and deformation of propeller

5 结 语

1)螺旋桨是复杂的曲面结构，应用相应三维软件进行建模，并划分分区混合流体网格和结构网格。计算精度较高，能准确的预报螺旋桨的水动力性能。

2)采用CFD 软件使用MRF 转动模型和SST 湍流模型完成螺旋桨的流体分析，得到在不同进速下的推力系数、扭矩系数及敞水效率，并将计算值与试验值进行比较，结果吻合较好。根据计算值，分析了桨叶上的总压分布随着进速系数的变化趋势，并对桨后尾流进行了考察。

3)通过Workbench 软件平台实现了螺旋桨流固耦合的数值计算。对螺旋桨在流场中工作时的强度进行了校核，并总结出桨叶最大变形，最大应力和进速系数在一定范围内存在线性关系的规律，对深入研究具有一定的参考价值。

［1］KO YAMA K．Comparative calculations of propeller by surface panel method-workshop organized by 20th ITTC propulsion committee［J］．Papers of Ship Research Institute，1993，15:57－66．

［2］YOUNG Y L．A BEM for prediction of unsteady mid－chord face and/ or back propeller cavitation［J］．Journal of Fluids Engineering，2001，6(123):311－319．

［3］王国强，董世汤．船舶螺旋桨理论与应用［M］．哈尔滨:哈尔滨工程大学出版社，2009．

［4］王超，黄胜，解学参．基于CFD 方法的螺旋桨水动力性能预报［J］．海军工程大学学报，2008，20(4):107－112．

WANG Chao，HUANG Sheng，XIE Xue-shen．Hydrodynamic performance prediction of some propeller based on CFD［J］．Journal of Naval University of Engineering，2008，20(4):107－112．

［5］张帅，朱锡，侯海量．船舶螺旋桨流固耦合稳态求解算法［J］．哈尔滨工程大学学报，2012，33(5):615－621．

ZHANG Shuai，ZHU Xi，HOU Hai-liang．Computation algorithm of fluid-structure interaction of marine propellers in steady state［J］．Journal of Harbin Engineering University，2012，33(5):615－621．