深水自升式钻井平台动静响应分析及疲劳寿命预测

朱 文，唐文献，刘永强，邓成斌，丁 浩，王芝明

(1.江苏科技大学 机械工程学院，江苏 镇江212003;2.海鹰企业集团有限责任公司，江苏 无锡214061)

0 引 言

陆地上油气资源日益枯竭，世界范围内的油气勘探与开发已经转向广袤的海洋。自升式平台由于其造价相对较低、操作性较强，成为目前应用最广泛的海上移动钻井设施。随着海洋工程不断向深海发展，海洋环境变得更加恶劣，各种不确定因素剧增，为了保证平台及工作人员的安全，钻井平台结构的安全性与稳定性受到越来越多的重视［1］。因此，必须对自升式平台的结构进行强度校核。另外，随着工作水深的增加，桩腿长度不断加长，平台柔性越来越大，其动力效应也越来越明显［2-3］。CCS 《海上移动平台入级与建造规范》中规定，当工作水深超过100 m 时，自升式平台的设计应考虑波浪的动力效应。

本文以中集集团某型桁架式自升式钻井平台为例，结合平台自身结构特点，对有限元分析模型建立的关键技术进行详细介绍;基于大型通用软件Ansys，结合载荷最不利组合原则，对风暴自存和正常作业2种典型工况下平台的结构强度与稳定性进行了分析计算;通过Newmark 逐步积分法对随机波浪力作用下的平台结构进行瞬态动力分析，得到平台受力与变形等瞬态响应结果。最后，对平台结构进行随机振动分析，并根据Steinberg 提出的基于高斯分布和Miner 线性累计损伤定律对平台进行随机疲劳计算，预测该平台的随机疲劳寿命。为不同类型自升式钻井平台的强度校核与寿命预测提供技术参考。

1 数学模型及计算载荷

1.1 平台设计参数

该型桁架式深水自升式钻井平台主要由船体、桩腿和齿轮升降组成。主船体采用三角形箱体结构，首一尾二。平台的结构参数和环境条件如表1所示。

表1 平台结构参数Tab.1 Platform structural parameters

1.2 有限元模型

平台有限元模型的精度直接关系到整个平台静动力分析结果的准确性。相对于静力分析，动力响应分析更需要保证模型刚度、阻尼、载荷及质量矩阵与实际情况一致。建立模型中需要处理好以下几个关键问题:甲板主船体的刚度，桩腿的模拟、桩腿与甲板主船体的连接方式以及桩靴的处理方式。其中，桩腿的模拟及桩腿与船体连接方式的模拟最为关键。平台结构的有限元模型如图1所示。

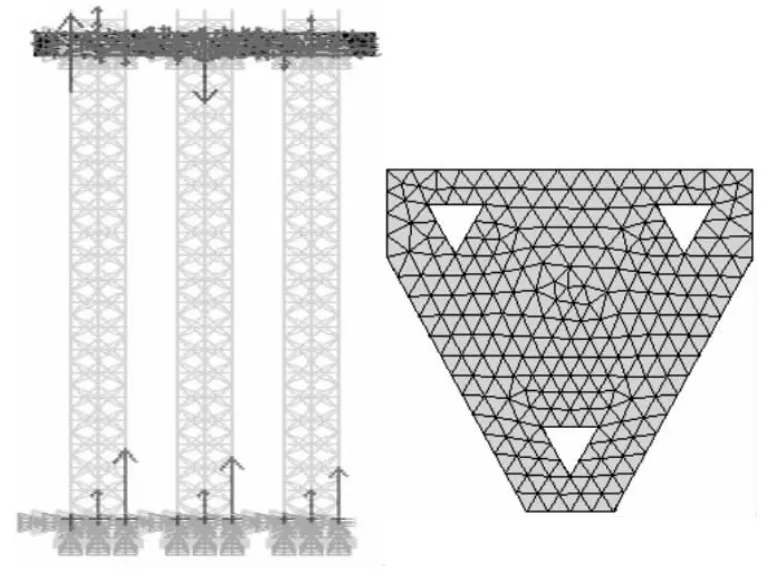
图1 平台有限元模型Fig.1 Finite element model of Platform

1.2.1 桩腿的模拟

桩腿是自升式平台中最为重要的部分，对平台的安全起决定性作用。为了保证弦杆刚度特性的真实性及水动力系数CD和CM的计算精度，模拟计算中，桩腿各弦杆采用PIPE16 单元和PIPE59 单元进行模拟，前者用于模拟平台中不考虑流体效应的管体结构，而后者适用于泥线以上考虑波流等流体效应的海洋管体结构。

1.2.2 桩腿与船体连接的模拟

桁架桩腿与甲板主船体的连接方式直接影响有限元分析结果的准确性。动力分析模型中需充分考虑桩腿和船体间的连接刚度，因此，利用弹簧单元模拟桁架桩腿与甲板主船体间的连接。弹簧刚度系数的计算方法如下式［4］:

式中:Kry，Krz，Kv为桩腿与甲板主船体的y，z 方向扭转刚度系数和垂向位移刚度系数;A 为桩腿截面的面积;Kv_fix为锁紧系统的垂向位移刚度系数;Kry_fix，Krz_fix和Kry_leg，Krz_leg分别为锁紧系统及桁架桩腿的扭转刚度系数，其计算方法如下:

式中:Ileg_y和Ileg_z为导向结构间桁架桩腿的截面惯性矩;L1和L2分别为锁紧系统垂向长度和导向结构距离锁紧系统长度。

1.3 平台载荷的确定

平台载荷主要包括平台功能载荷和环境载荷。功能载荷主要包括自重、设备重量和平台相关的载荷以及其他生活供应品等，可通过点、线、面方式进行加载;对于可变工作载荷，可采用质量单元进行集中加载;其他如甲板工作载荷等，可直接施加压力载荷。环境载荷主要包括风、浪、流载荷，通过CCS 中国船级社规定确定其大小;环境载荷的作用方向根据Ansys 软件波浪相位角搜索程序确定。

2 平台静力计算结果分析

平台总体性能的分析，重点是为了考察桩腿的结构强度、桩靴的承载能力、升降锁紧系统的强度和承载能力以及整体结构的抗倾稳性等［6］。计算中，船体和桩腿的材料特性如表2所示。

表2 材料参数Tab.2 Material parameters

2.1 风暴自存工况下结果分析

风暴自存工况比较复杂。由于波浪具有随机性，所以环境载荷有多种不同的组合状态。根据CCS 相关规定，计算载荷需按照最大静重力、风、浪、流等最不利情况进行组合。此时，平台的分析结果如图2所示。

图2 风暴自存工况下等效云图Fig.2 Equivalent diagram of storm-deposited condition

分析图2 可知，风暴自存工况下平台最大变形量为0.039 3 m，位置位于平台顶部;平台结构最大应力为230 MPa，位置位于桩腿与船体的连接处。经分析，此时桩腿强度满足设计要求。

2.2 正常工作工况下结果分析

正常作业工况应考虑供应品、燃料等各种生活物资以及设备的满载情况;同时，必须满足钻井操作、船体重量突然改变、有集中载荷与竖立钻杆等各种重量变化的情况。按照最不利载荷组合进行计算，其分析结果如图3所示。

图3 正常工作工况下等效云图Fig.3 Equivalent diagram of normal-working condition

由图3 可知，正常工作工况下平台最大位移为0.025 8 m，发生在平台顶部;平台结构最大应力为231 MPa，也发生在桩腿与船体连接处。经分析，正常工作工况下桩腿的设计强度满足要求。

3 波浪作用下平台动力响应分析

3.1 模态分析结果

模态分析用于确定系统的振动特性，是平台结构动态性能分析的起点，对进一步研究平台结构在随机波浪力作用下的动力响应和预测疲劳寿命有重要的意义。平台结构属大型工程结构，其自由度虽然很多，但往往激励的高频成分很弱或是系统的高频成分对振动的贡献度很低［8］，所以表3 只列举了平台前6 阶模态的固有频率。

表3 固有频率(Hz)Tab.3 Natural frequency(Hz)

3.2 波浪作用下平台的瞬态动力响应

采用Newmark 逐步积分法，并结合Stokes 五阶波理论对波浪力进行计算，其中，波浪周期14.1 s，波高16.8 m，作用时间为100 s，时间间隔为0.2 s。通过Ansys 瞬态动力学分析，计算平台结构在任意波浪载荷作用下的动力响应，得到了平台在各载荷随意组合作用下随时间变化的位移、应力等响应曲线，如图4和图5所示。

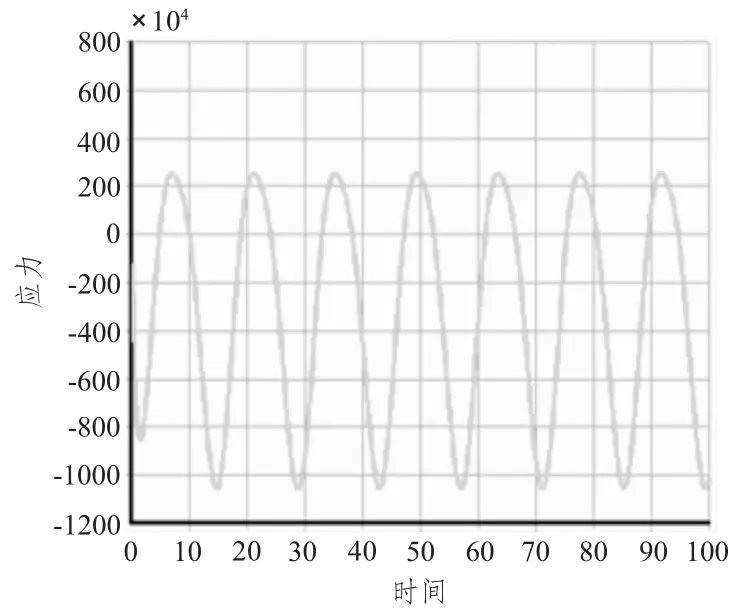
图4 弱节点29 处的时间-应力曲线Fig.4 Stress-time history curve of node 29th

由图4和图5 可知，在t=10 s 后，结构振动趋于稳定;平台应力和位移的最大响应值均出现在15 s左右，此时平台的动力响应明显，其等效云图如图6所示。

此时结构最大应力为346 MPa，最大位移为0.043 m。与线性静力分析结果对比发现，平台在波浪载荷作用下，x 方向响应较大，y 方向相对较小，且位移和应力均显著增大。

由于桁架式自升式平台柔性较大，在动载荷作用下平台响应结果较静力分析明显偏大，因此，不允许仅对自升式平台进行静力分析，需在静力分析的基础上进行动态分析，以确保平台的安全性与稳定性。

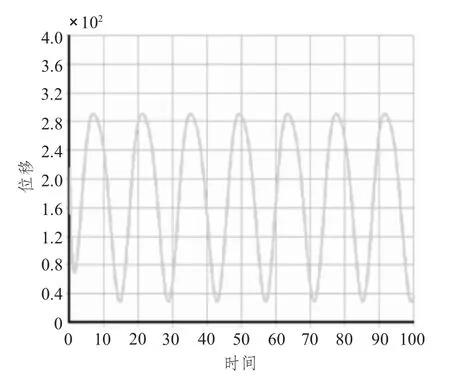
图5 弱节点29 处的时间-位移曲线Fig.5 Displacement-time history curve of node 29th

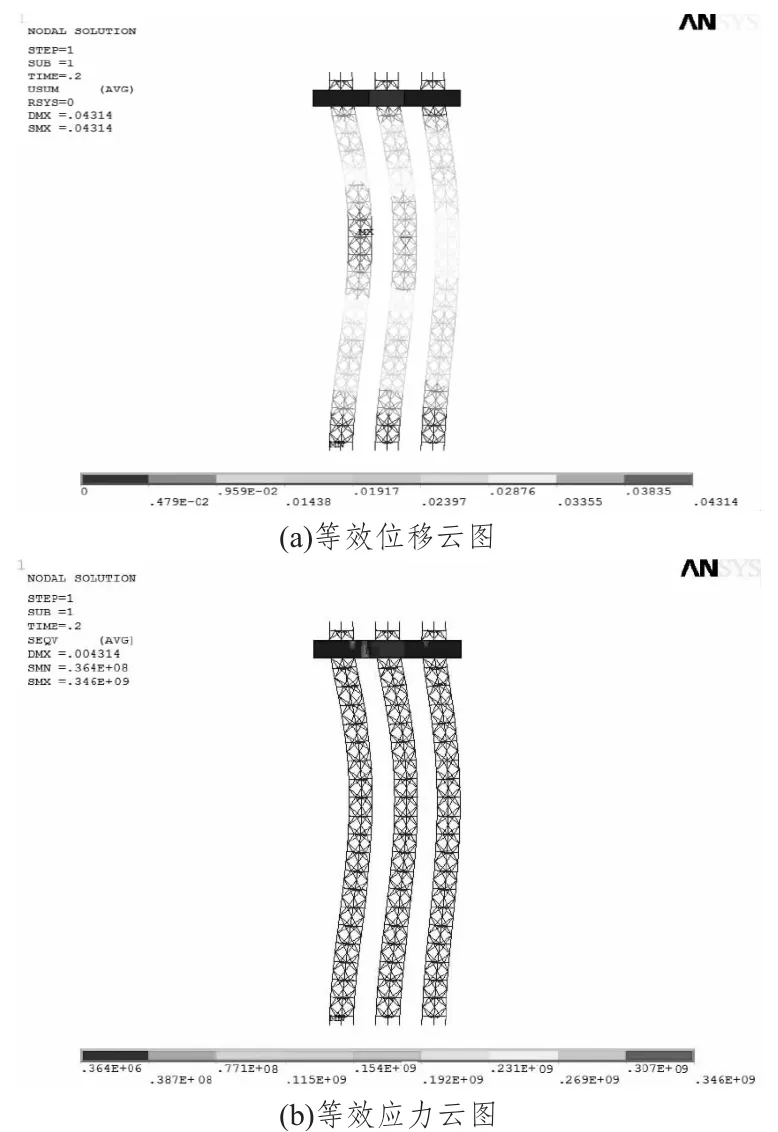
图6 等效应力和位移云图Fig.6 The equivalent displacement and stress diagram

3.3 波浪作用下平台的随机振动响应

随机振动分析主要用于确定结构在具有随机性质的载荷作用下的响应。采用频域法进行分析［9-10］，利用频谱分析法，将波浪谱作为输入谱，通过计算获得频域传递函数，得到结构响应的输出谱，以此描述响应的应力信息，即:

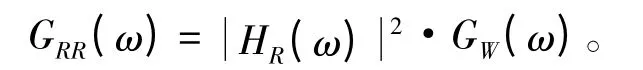
式中:GRR(ω)为平台响应输出谱;为频率传递函数;GW(ω)为波能谱。

波浪力谱曲线如图7所示。

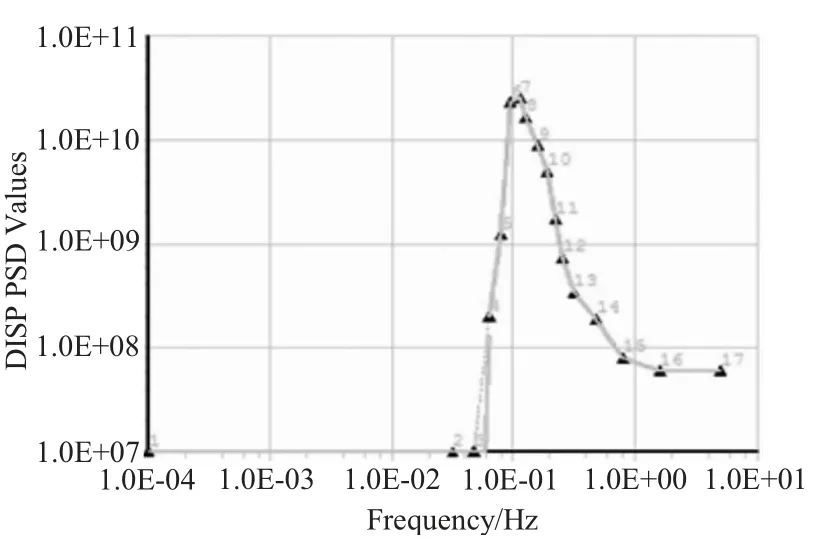
图7 波浪力谱曲线Fig.7 Spectrum curve of wave force

通过Ansys 计算平台在波浪载荷作用下的随机振动响应，得到其谱值与频率的关系曲线如图8和图9所示。

图8 46#节点Y 方向的位移响应曲线Fig.8 The displacement response curve of node 46th in the Y direction

分析图8和图9 可知，功率谱密度曲线均出现2 个峰值，结合波浪谱曲线及模型的固有频率可以看出，第1 个波峰值产生的原因是因为该峰值频率(1.212 Hz)处在结构前3 阶固有频率附近，此时会引起结构的强烈共振，结构响应出现极大值;第2 个峰值的出现是因为波浪谱在该频率处呈现极大值。

图9 46#节点Y 方向的速度响应曲线Fig.9 The velocity response curve of node 46th in the Y direction

3.4 平台的随机疲劳寿命计算

环境载荷的持续作用会使平台结构产生交变应力，进而引发平台结构的疲劳损伤。当疲劳损伤积累到一定程度后，结构将会产生疲劳破坏。在影响平台疲劳损伤的众多环境载荷中，波浪是导致疲劳破坏的主要载荷。

通过前面的计算与分析发现，载荷步1σ 的最大Von Mises 应力值为230 MPa。根据Steinberg 提出的基于高斯分布和Miner 线性累积损伤定律的三区间法进行疲劳计算，假设结构的振动时间(期望的寿命)T=4.38×105h，振动的平均频率为次，则:

根据文献［11］淬火调制钢ASTM-A517GRQ 的P-S-N 曲线查得:应力1σ=230 MPa 时，N1σ=+∞;应力2σ=460 MPa 时，N2σ=+∞;应力3σ=690 MPa 时，N3σ=+∞。将上述数值代入总体损伤计算公式，得到:

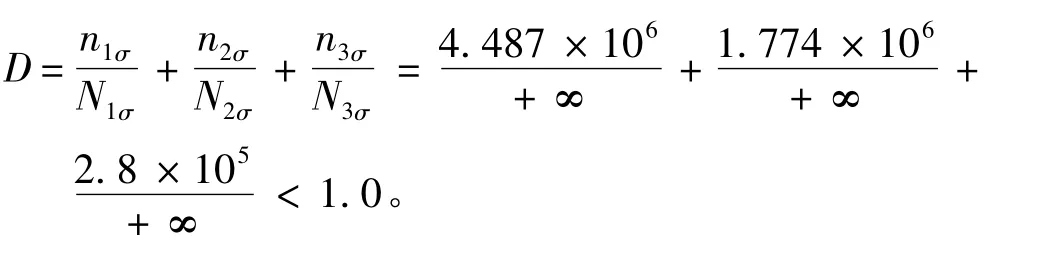
通过上述计算，说明该自升式钻井平台的工作寿命超过50年，满足寿命设计要求。

4 结 语

1)桩腿的结构形式和尺寸对平台结构的刚度和强度影响较大;桩腿是平台中较为薄弱的部分，设计时安全系数应取较大值。

2)桩腿和平台整体结构均满足强度设计要求，最大应力均出现在桩腿和船体连接处，此处为强度评估的重要部位。

3)波浪力作用下，平台瞬态响应结果呈现随波浪周期变化的趋势;随机振动结果表明结构低阶固频附近的振动，会引起较大的速度和位移响应，设计中应尽量避开此类低频振动。

4)采用随机波浪谱分析法对平台进行随机疲劳寿命预测，结果表明该平台工作寿命超过50年，满足规范要求。

［1］李润培，王志农.海洋平台强度分析［M］.上海:上海交通大学出版社，1992.

［2］CASSIDY M J，et al.Evaluation of long-term extreme response statistics of jack-up platforms［J］.Ocean Engineering，2002，29:1603-1631.

［3］HAMBLY E C，IMM G R，STAHL B.Jackup performance and foundation fixity under developing storm contions［A］.OTC 6466，1990.

［4］MSC.Overall basic design for jack-up［M］.Gusto MSC，2007.

［5］李红涛.自升式移动平台结构动力响应研究［J］.中国海洋平台，2011，26(3):12-16，29.

LI Hong-tao.Study on structure dynamic response analysis of jack-up units［J］.China Offshore Platform，2011，26(3):12-16，29.

［6］中国船级社.海上移动平台入级与建造规范［S］.北京:人民交通出版社，2005.

［7］Technical ＆ Research Bulletin 5-5A.Guidelines for site specific assessment of mobile Jack- up units［S］.The Society of Naval Architects and Marine Engineers，1994.

［8］胡桃华.全液压履带装载机车架结构有限元分析及优化设计［D］.同济大学，2009.

［9］窦培林，杜训柏，胡礼明.基于随机波浪谱对深水区自升式平台动力响应分析［J］.中国海洋平台，2009，24(6):25-30.

DOU Pei-lin，DU Xun-bai，HU Li-ming.Dynamic response analysis of deep-water jack-up platform based on random wave spectrum［J］.China Offshore Platform，2009，24(6):25-30.

［10］吴小平，陆晟.自升式钻井平台环境载荷及结构强度［J］.上海造船，2010，3:36-40，51.

WU Xiao-ping，LU Sheng.Environmental loading and structure strength of self-elevating drilling units［J］.Shanghai Shipbuilding，2010，3:36-40，51.

［11］材料手册编写组.机械工业常用材料性能数据手册［M］.北京:机械工业出版社，1994.