仿真潜艇航向对规避航空磁探仪搜索的影响

曲晓慧，娄树理，王传芳，陈 玫

(1．海军航空工程学院，山东 烟台264001;2．青岛科技大学，山东 青岛266061)

0 引 言

由于潜艇在地磁场中建造和运动，潜艇的永久磁场和感应磁场无法消除，因此可以利用潜艇的磁特性进行搜潜。航空磁探仪(MAD)具有不受水文气象条件限制、可连续搜索、搜索效率高、使用简单可靠、反应迅速、定位精度高、隐蔽性好、探测距离较近等特点［1］，利用其搜潜是目前航空反潜的重要手段。对于潜艇来说，如果已知磁探仪在对其搜索，就要立即采取规避措施，例如下潜至更深的位置，改变其航向等。而应以何种航向航行能最有效地规避搜索是值得研究的问题。本文利用蒙特卡罗法对潜艇不同航向时被航空磁探仪搜索到的概率进行仿真研究，为实际规避过程提供指导。

1 航空磁探潜数学模型建立

1.1 航空磁探仪所测磁异常信号的分析

在研究潜艇磁场过程中，当测量点距目标距离与目标尺寸之比大于一定值时，潜艇引起的磁场可等效为磁偶极子磁场［2］。如图1所示，图中位于S点的磁矩为M 的磁偶极子会在矢量r 处的P 点产生磁场Hr，由电磁学原理可知，这个磁场可表示为［2］:

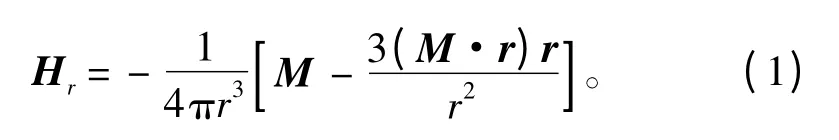
式中:M 为潜艇磁矩，A·m2;r 为测量点至潜艇的距离矢量，m;Hr为潜艇在测量点产生的磁场强度，A/m。

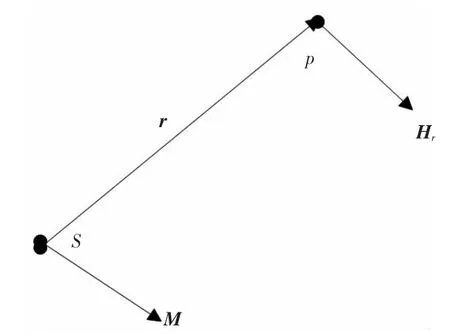
图1 潜艇磁矩M 产生的磁场HrFig.1 Magnetic field Hr caused by submarine magnetic moment M

用光泵式或核磁旋进式磁强计测到的是总磁场，它包括没有目标时的地磁场和目标产生的偶极场之和。总磁场可表示为:

式中:HT为所测到的总磁场;HE为测量点的地磁场，如图2所示。

由已有的实验测试可知，潜艇产生于飞机磁探仪处的磁场Hr约为1 ～2 nT，地球磁场HE则达40～50 μT。由于潜艇的偶极场很小，所以总场方向很接近地磁场，即δ 角很小，而磁探仪测量的是总磁场HT并经滤波除去其中的恒定分量HE，所以磁探仪测得的磁异常信号实际上是潜艇磁场在地磁场方向上的投影值。即

其中iE为地磁场方向的单位矢量。

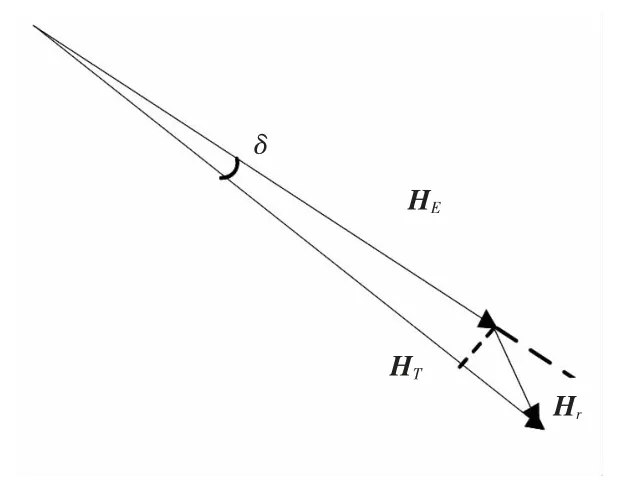
图2 HT 与HE 及Hr 的关系Fig.2 The relation between HT、HE and Hr

可见，磁探仪测得的磁异常信号实际上是潜艇磁场在地磁场方向上的投影值。将式(1)代入式(3)可得:

由于磁探仪测量的物理量是磁感应强度B，由磁场强度和磁感应强度的关系可知磁探仪探测到的潜艇产生的磁异常信号为:

式中μ0=4π×10－7H/m，磁感应强度B 的单位为T(特斯拉)。由于这个单位非常大，航空磁探中多使用nT 作为单位(1nT=10－9T)。

1.2 (x，y，z)坐标系下的磁场表达式

直接建立航空磁探潜的数学模型比较困难。本文首先建立以潜艇为坐标原点的(x，y，z)坐标系，如图3所示。其中xoy 平面是水平面，iE为实际地磁场方向的单位矢量，它的特点是指向水平面下，其在水平面上的投影(称为磁北)与地球北极存在一定角度的偏差，这个角度称为磁偏角。iE与它在水平面上的投影之间的角度θ 称为磁倾角。为了分析方便，以磁北为x 轴的正方向，与水平面垂直的方向为z 轴，向上为正，以与xoz 平面垂直的方向为y 轴，以右手螺旋法则指向的方向为正。潜艇的航向(艇首与磁北的夹角)为φ，以逆时针方向为正(从飞机上向下看);潜艇的纵轴方向的磁矩为Ml，指向艇首为正;潜艇横轴方向的磁矩为Mt，指向艇右为正;潜艇竖直方向的磁矩为Mv，向上为正［3］。

由图3所示坐标系可建立如下方程:

其中:

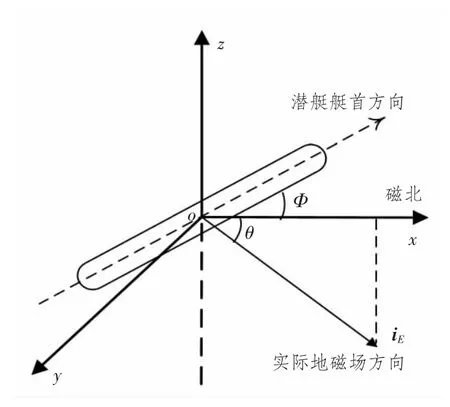
图3(x，y，z)坐标系Fig.3 Coordinate system of(x，y，z)

式中r 为测量点(x，y，z)到潜艇的距离矢量。

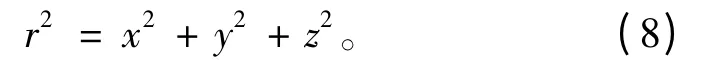
将式(6)和式(7)代入式(5)得:

其中:

式(9)和式(10)即为(x，y，z)坐标下的潜艇磁场表达式。

1.3 (E，D，β)坐标系下的磁场表达式

图4 表示探潜飞机正沿着直线AF 飞行执行搜索任务。垂直于AF 线，并通过潜艇所在点S 的平面，被称为垂直目标平面(Vertical Target Plane)。B 点是AF线与该平面的交点，该点是该段航线上飞机最接近潜艇之处，由BS 决定的D 可称之为斜距，D 的值恒为正。由距离AB 决定的E 表示飞机至垂直目标平面的距离，E 的正方向为飞机飞行方向。由B 点作垂直于潜艇所在水平面的直线BC，由该直线转到BS 线的角度β称之为航偏角，以顺时针方向为正(从飞机上看时)，C 点为B 点在潜艇所在水平面的投影点，BC 之间的距离即磁探仪所在水平面与潜艇所在水平面的距离为d。由D和β 的值决定CS 的距离。(E，D，β)坐标系即为探潜坐标系。

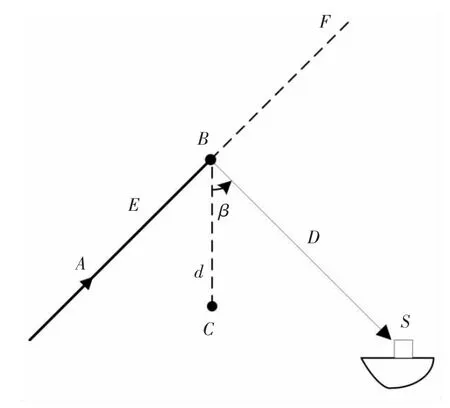
图4 搜潜坐标系Fig.4 Coordinate system of searching submarine

若假设α 为AB 在xoy 平面上的投影与x 轴的夹角，由飞机的航向决定，以顺时针为正，则可得探潜坐标系(E，D，β)与(x，y，z)坐标系的转换关系如下:

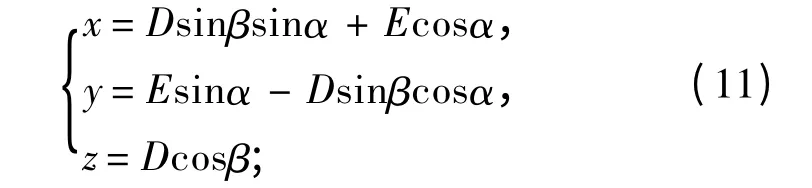
且

将式(11)和式(12)代入式(10)可得到(E，D，β)坐标系下A1，A2，A3的表达式，和式(9)一起构成了(E，D，β)坐标系下的磁场表达式。

如果不考虑磁噪声的影响，通过这个数学模型可以得出在某种情况下航空磁探仪探测到的信号形式如图5所示。

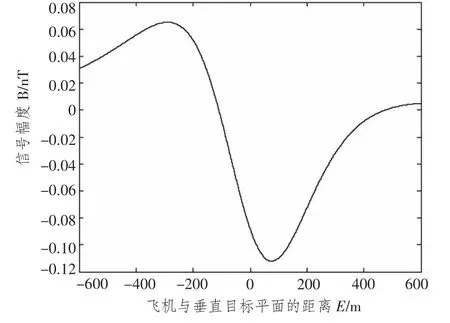
图5 航空磁探仪探测到的信号Fig.5 The signal detected by airborne MAD

2 潜艇航向对规避磁探仪搜索的影响

潜艇航向对规避磁探仪搜索的影响可以用潜艇不同航向时飞机搜索到的概率来体现，即对某一次搜索来说，潜艇的航向已知，飞机与潜艇之间的相对位置随机，飞机以任意航向飞行搜索。利用蒙特卡洛法仿真飞机任意5 000 次飞行中搜索到潜艇的概率，潜艇被搜索到的概率最小的方向即为规避时航行的方向。

2.1 蒙特卡罗法

蒙特卡罗法也称统计试验法。其基本思想是:针对要求解的数学、物理、工程技术以及生产管理等方面的问题，首先建立一个该问题随机过程的概率模型，确定问题解的指标;然后通过对模型或过程的观察或抽样试验，来计算解的指标的统计特征，给出解的近似值。利用蒙特卡罗方法解题的关键，首先要建立与实际问题有相同概率特性的简单而易于实现的概率模型，其次要产生与实际因素有相同变化规律的随机数。这种方法常用来解决较复杂的随机过程。在解决某些复杂的军事运筹学、作战模拟问题时，统计试验是一种基本有效的方法。而且研究表明，过程中随机因素愈多，就愈适合采用蒙特卡罗方法［4］。

在研究磁探仪搜潜概率问题中，随机因素有:潜艇航向φ，磁探仪所在水平面与潜艇所在水平面的距离d，航偏角β。

2.2 潜艇航向对规避磁探仪搜索影响的仿真分析

由图4 可知，如果给定BC 的距离和航偏角β，SC 之间的距离就确定了。仿真分2 种情况:一种是β∈(－5π/12，5π/12)，即SC 之间的最大距离为d·tan(5π/12);另一种是缩小搜索范围，β∈(－π/3，π/3)，即SC 之间的最大距离为d·tan(π/3)。

仿真条件:地磁倾角θ=30°，d 为(200，250)中的任意值，单位为m，则D=d/cosβ，由于飞机的航向未知，所以α 为(0，2π)中的任意值。潜艇磁矩为:Ml=60 000，Mt=2 000，Mv=20 000，单位为A·m2。当飞机飞行时，即E 的值由－600 ～600 m 的过程中，如果磁探仪检测信号的最大值和最小值之差大于0.1nT(一般磁探仪的灵敏度)就认为检测到了潜艇。蒙特卡洛仿真次数为5 000 次。

仿真结果:β ∈(－5π/12，5π/12)和β ∈(－π/3，π/3)时潜艇的航向角φ 与航空磁探仪搜潜概率之间的关系分别如表1和表2所示。

表1 β∈(－5π/12，5π/12)时潜艇航向与磁探仪搜潜概率的关系Tab.1 The relation between submarine navigational orientation and searching submarine probability when β∈(－5π/12，5π/12)

表2 β∈(－π/3，π/3)时潜艇航向与磁探仪搜潜概率的关系Tab.2 The relation between submarine navigational orientation and searching submarine probability when β∈(－π/3，π/3)

由表1和表2 可以看出，当潜艇的航向为90°和270°时，潜艇被搜索到的概率最小。结合图3 的坐标系可知，航向90°和270°意味着潜艇东西向航行。当搜索范围缩小后，航空磁探仪搜索潜艇的概率增加了，这与其他文献的仿真结果一致［5］。

由仿真结果可以得出这样的结论，当潜艇需要规避航空磁探仪搜索时，应东西向航行。

3 结 语

本文将潜艇看做一个磁偶极子，在建立了以潜艇为中心的(x，y，z)直角坐标系的基础上，建立了航空磁探仪搜潜的(E，D，β)坐标系，并利用蒙特卡洛法对潜艇不同航向时的磁探仪搜潜概率进行仿真。结果表明，潜艇在规避航空磁探仪搜索时应尽量东西向航行，这对实际的规避过程具有理论指导意义。但是本文仿真的搜潜过程是在假设潜艇航行速度相对飞机搜索速度来说很小的情况下，即在搜潜的过程中潜艇假设为不动的基础上。如果潜艇的速度与飞机的速度相比不是很小，就不能用本文所建立的(E，D，β)坐标系下的数学模型来仿真搜潜概率，需要建立新的数学模型［6］。另外，本文没有考虑磁噪声的影响，这些都是需要继续研究的地方。

［1］屈也频．反潜巡逻机搜潜辅助决策系统研究［D］．长沙:国防科学技术大学，2009:14－15．

［2］翁行泰，曹梅芬，吴文福，等．磁异探潜中潜艇的数学模型［J］．上海交通大学学报，1995，29(3):27－32．

［3］林春生，龚沈光．舰船物理场(2 版)［M］．北京:兵器工业出版社，2007:31－37．

［4］张艳，黄敏，赵宇．基于置信分布的系统可靠度评估蒙特卡罗方法［J］．北京航空航天大学学报．2006，9(9):1023－1025．

［5］张尧卿，王光源，林芳慧．反潜巡逻机磁探仪检查搜潜效能研究［J］．兵工自动化，2012，31(6):4－6．

［6］李居伟，徐以诚，孙明太．航空磁探仪目标运动分析仿真研究［J］．指挥控制与仿真，2011，33(4):72－74．