脐带缆对水下航行器动态响应的影响评估研究

章浩燕，朱克强

(宁波大学，浙江 宁波315211)

0 引 言

目前，由于无缆自主式有人或无人潜水器等深水工作系统在动力供应、数据传输、安全性、可靠性等方面还存在不少难以解决的问题，所以采用脐带缆控制的潜水器在世界上仍然广为使用［1－4］。脐带缆控潜水器能够安全有效地到达海洋深水区域，是深海作业的重要工具。操作员可以安全地呆在甲板上操纵潜水器，有效地完成危险环境下的作业任务。岸上平台与潜水器之间通常由1 根脐带缆连接，该缆索内部有光电传输芯线，用于向ROV 传输动力并保持可靠联系，芯线外面由一层保护层包围，用来承载水下单元和保护缆索内部芯线。由于它的动力是由支援船提供，所以潜水器原则上可以无限停留在海底作业地点。

缆索在带来优点的同时也产生了如下几个急需解决的难题:

1)实际操作和测量数据证明，系统主导运动是垂向运动，在靠近谐振频率附近操作时，笼的升沉运动甚至要大于母船。在剧烈海况下，较大的垂向运动会导致罐笼附近的缆索瞬间松弛，而缆索再次收紧时，运动加速度可达0.5 g，从而产生巨大瞬间突变载荷，可导致脐带缆保护层及其内部光电传输芯线结构的破坏，缩短脐带缆的寿命，甚至切断信息和能源的传送，潜水器也就无法操作并危及它的回收。海况恶劣时，罐笼产生较大的垂向运动也会使潜水器入坞和回收困难。故该系统通常只能局限在平静海况下使用。

2)脐带电缆为潜水器提供动力和传输信息的同时，会增加潜水器的航行阻力(25 mm 直径1 m长的缆索可以产生与0.5 m 直径，3 m 长的拖鱼同样的阻力)，缆索阻力会影响潜水器推进的动力需求，动力的增加反过来又需要更大的缆索直径从而产生更大的阻力，这是一个典型的非线性设计环路问题。如果在设计中规定了系缆潜器的水下航速，或实际顶流能力，那么为了确定潜水器推进功率和运动姿态，就必须精确计算脐带缆作用在潜器上的拉力大小。预报缆索最佳长度以使总阻力最小化。

3)缆索除了增加阻力外，还会发生脐带电缆与后退、下沉中的ROV 本体或其他海底物件的纠缠，这是实际中最常见的事故。轻微的纠缠可能造成短暂的耽搁，比较严重的纠缠则可能导致潜水器弃置几个月，甚至丢失。缠绕的重要原因是操作者无法察觉脐带的形状，以判断哪些作业位置是否可以达到，或即使达到了，但潜器的姿态是否可以作业。这就要求实时计算出缆索动态构形。

对于许多海洋缆索系统，尤其是潜水器脐带电缆，在边界附近都存在着初始或潜在低张力区，触底点附近完全挠性缆的张力为0。当缆索底端重物触底时，缆索张力将急剧减少，引起整个系统的松弛。在缆索急速放出过程中，水面船状态发生急速操纵，速度的变化也会引起缆索短暂的失去张力。不能采用目前广为使用的完全挠性缆索连续模型，因为有数学奇异性的存在。虽然研究表明，在连续模型加入微小的弯曲刚度就能捕获曲率、剪力的急剧变化，从而精确模拟低张力区缆索的运动特性。在缆索模型中计入的弯曲刚度附加值虽然很小，但却能使得能量越过低张力区，消除零张力区的奇异性，提高解的稳定性，但由于求解效率较低，往往需要将弯曲刚度影响较大的区域与缆索其他的区域分开来提高求解的效率。

本研究对系统建立三维空间运动通用数学模型，可以全面反映脐带缆－潜水器多体之间的非线性耦合运动;非均匀脐带缆运动考虑为三维，能真实地反映缆索的各种非均匀性，适应较复杂的潜器机动状态;为了克服柔性缆在大曲率——时间变化率时的易于发散性，采用自动变步长数值积分技术，以模拟比较复杂的耦合运动响应。由于对系统建立了最一般的空间运动模型，反映了二者的耦合运动，从而更加接近实际，可为进一步研究系统闭环特性提供基础。

1 缆索的动态响

1.1 坐标系建立

为了分析缆索运动及其对航行器的影响，建立3 套坐标系:地面坐标系，缆索的局部坐标系及航行器运动坐标系。设地面标系(i，j，k)，原点设为E;航行器运动坐标系(iv，jv，kv)以航行器的质心G作为坐标原点，纵轴iv平行于航行器的横摇轴并指向航行器前进方向，横轴jv平行于纵摇轴并指向右舷。航行器运动坐标系与地面坐标系之间的关系可以用欧拉角的形式表示:

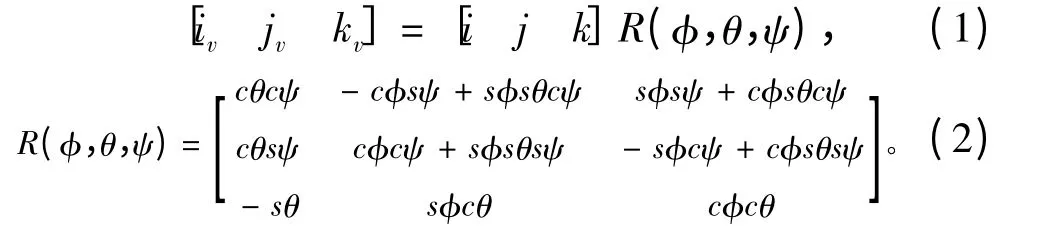
式中:c·=cos·;s·=sin·;φ，θ，ψ 分别为航行器的横摇角、纵摇角以及首摇角。

对横摇角φ，纵摇角θ，首摇角ψ 的定义如下:横摇角φ:jv与平面(i，k)之间的夹角;纵摇角θ:iv与水平面(i，j)之间的夹角;首摇角ψ:iv轴在水平面(i，j)上的投影与i 轴之间的夹角。局部坐标(τ，n，b)表示缆索上的某点，τ 表示缆索的切线方向，且指向缆索伸长的方向，b 在(i，j)平面内。该坐标系由地面坐标系通过以下3 次旋转得到:1)将坐标系(i，j，k)绕着k 轴逆时针旋转α 角，使得i 与平面(τ，n)平行;2)将步骤1 所得的(i，j，k)坐标系绕着i 轴顺时针旋转π/2，使得k 与b 轴方向一致;3)将步骤2 所得的(i，j，k)坐标系绕着b 轴旋转β 角，使得i，j 分别与τ，b 轴的方向一致。因此，缆索的局部坐标系与地面坐标系之间的关系可用下式表示:

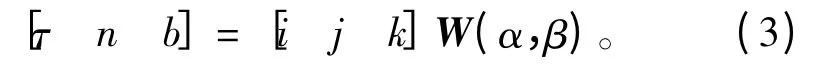
其中，

综合式(1)～式(4)，可以得到缆索的局部坐标系与航行器动态坐标系之间的关系为:

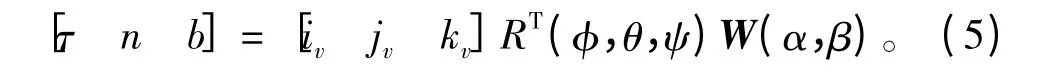
1.2 动力方程

定义速度:

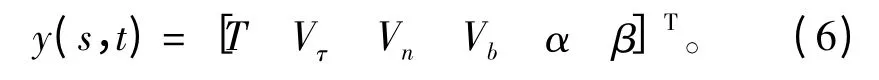
式中:t 为航行器运动时间;s 为从拖点开始的总弧长;T 为缆索内部张力;Vc=［VτVnVb］T为缆索某点处的速度向量。因此，缆索的动态方程可以用以下偏微分方程表示:

式中:ρ 为流体密度，kg/m3;m 为单位长度缆索的质量，kg/m;A 为缆索未伸长前的横截面积，m2;m1为单位长度缆索的实际质量，m1=m+ρA，kg/m;wc为水中缆索单位长度的重量，N/m;e 为1/EA;Ct为流体切向拖曳系数;Cn为流体法向拖曳系数;d 为缆索拉伸后的直径，m;J=［JτJnJb］T为用局部坐标系［τnb］为流体的顺势速度，m/s;U=［UτUnUb］为缆索的相对速度，U=Vc-J，m/s。

1.3 边界条件

为解得缆索的动态方程(7)，需要给出缆索的初始形态以及6 个边界条件。浸在水中的缆索有2个端头，即连接航行器的拖点端以及与岸上的滚筒端。由于缆索作用力直接影响拖点处的速度，于是得到3 个边界条件:拖点相对于航行器坐标系原点的矢径可以表示为rc=［xcyczc］T，航行器坐标原点相对于缆索坐标的运动速度可以表示为V=［uvw］T，其中(u，v，w)分别表示纵荡速度、横摇速度及垂荡速度，航行器绕其质心G 的转动角速度可以表示为Ω=［pqr］T，其中(p，q，r)分别表示航行器的横摇角速度、纵摇角速度以及首摇角速度。因此，在航行器坐标系中，拖点的速度可以表示为(V+Ω×rc)。式(5)中，拖点在缆索局部坐标系中的速度可以表示为:

上式为下端的3 个边界条件。由于滚筒对缆索主要产生切向的作用力，因此滚筒端部法向和副法线方向的速度为0:

其中St为t 时刻浸在水中的缆索总长。为了给出第6个边界条件，可以考虑缆索滚筒的滚动。由牛顿第二定律可以给出:

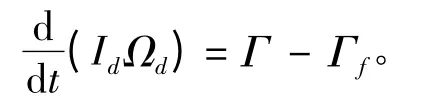
式中:Id为滚筒的转动惯量;Ωd为滚筒的角速度;Γ为缆索张力在滚筒端部产生的力矩;Γf为缆索枢轴与滚筒间滑动摩擦力产生的阻力矩。因为，Ωd=-Vt(St，t)/Rd;Γ=T(St，t)/Rd，其中，Rd表示滚筒的半径，滚筒的动态方程可以被重新写成:

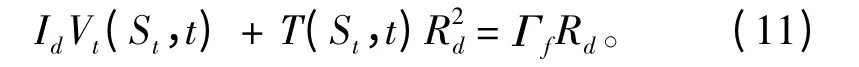
1.4 缆索的影响

缆索张力的初始值为T(0，t)t(0，t)，因此为了计算方便，可以将航行器受到的其他作用力通过式(5)在航行器运动坐标系中用张力表示如下:

其中，

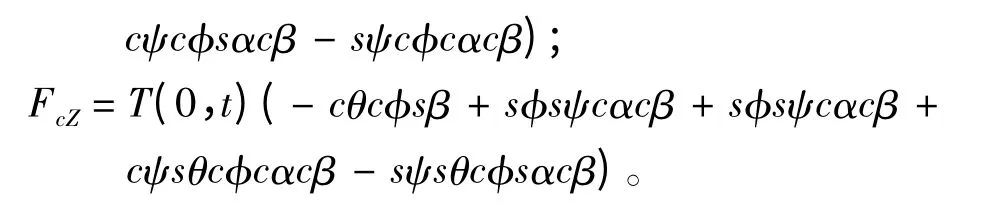
因此，在航行器动态坐标系中，缆索拖点处由缆索引起的力矩可以表示为:

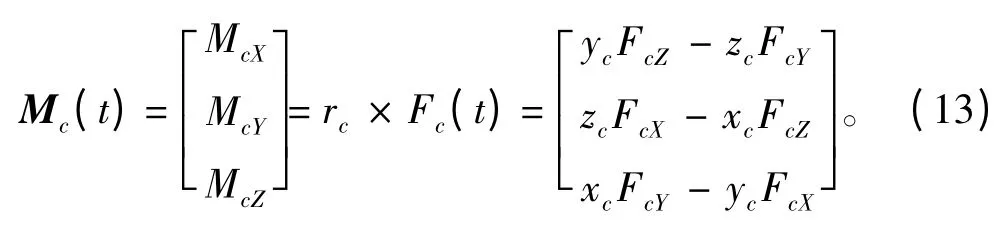
2 数值解法

在边界条件式(8)～式(11)下，解偏微分方程(7)的数值法可以采用差分方法，将方程按时间和空间离散化来处理。然而，和一般的拖曳系统不同的是，缆索的长度不再是定值，随着航行器前移，缆索的浸水长度逐渐增大。而且，t 时间内缆索浸水总长取决于缆索的切向速度- Vt(Sτ，τ)dτ，假设缆索浸水长度的初值为0，则

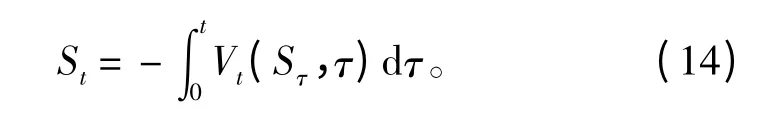
由于缆索长度随着时间不断变化，若将缆索分为多个片段，则片段的数目将随着拖曳时间的增加而增大，因此无法将缆索切分为定长度定数目的片段，然而差分格式只有每个片段的长度都固定的情况下才生效。将式(14)按时间步长Δt 进行离散化，即:

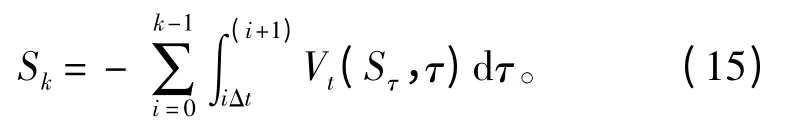
其中Sk(k=1，2，…)为kΔt 时间内缆索的总浸水长度。也就是说，kΔt 时间内的缆索浸水长度可以被切分为k 个缆索片段，其长度表示为:

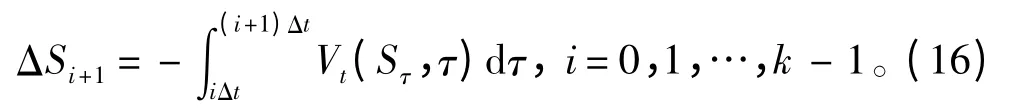
当Δt →0 时，缆索片段的长度可以近似为

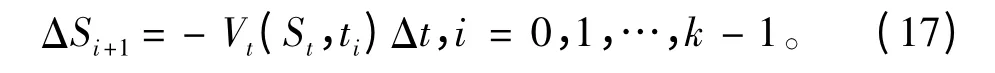
其中ti=iΔt，因此k 个缆索片段的长度可以由前一时刻的速度所确定。

综合式(15)～式(17)，可以得到

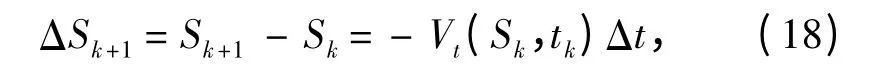
因此，k+1 时刻缆索的总浸水长度为

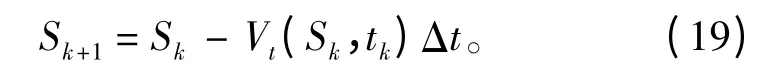
确定缆索片段的长度后，方程(7)可以用有限元二阶近似法进行求解。假设tk时刻，缆索的形态已知，即y(Si，tk)，i=0，1，…，k 已知，那么问题就转换为预测tk+1时刻缆索的形态，即求解y(Si，tk+1)，i=0，1，…k+1，其中，Sk+1由式(19)确定。

定义

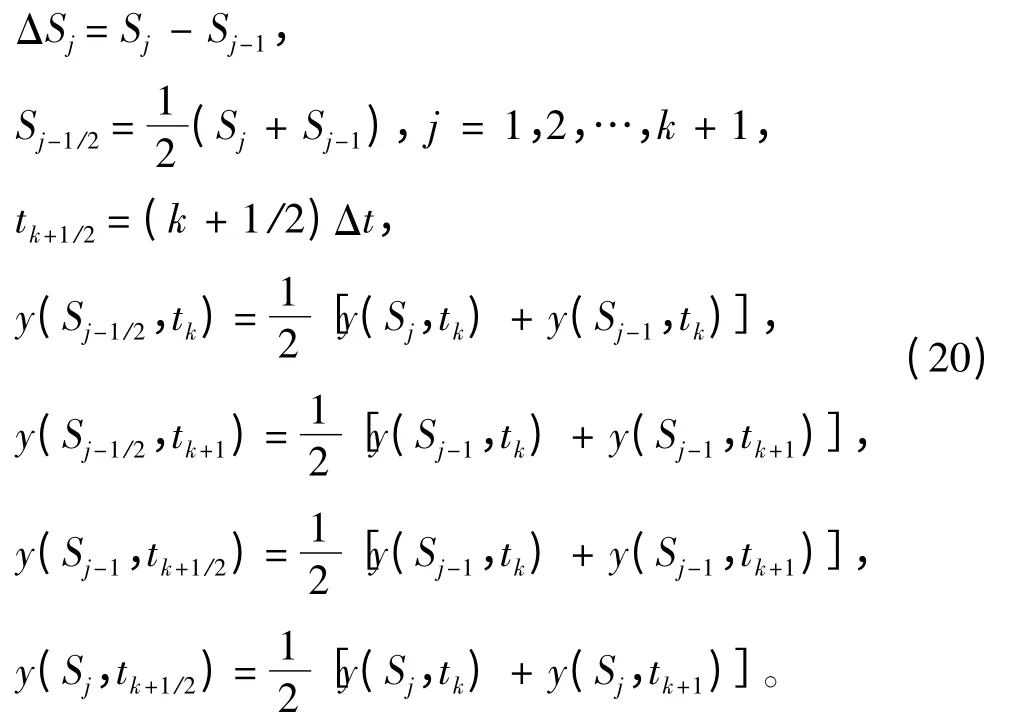
其中S0=0。注意到，由于ΔSk+1在tk时刻还未入水，式(21)中y(Sk+1，tk)由滚筒的滚动统一定义，即

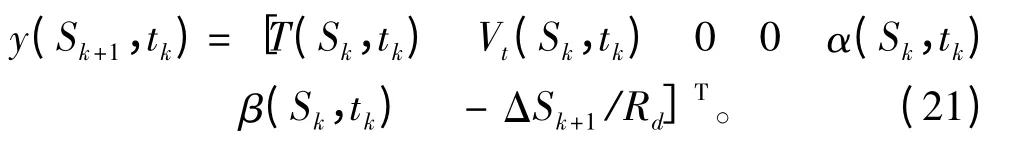
而且，方程(7)仍然可以用于求解新的入水片段的动态近似解，而且，当缆索浸水长度不大时，模型的误差可以忽略不计。应用方程(7)求解(Sj-1/2，tk+1/2)，j=1，2，…，k+1 的微分方程如下:

其中j=1，2，…，k+1。式(22)为j=k+1 时，缆索新入水片段的近似动态方程。剩余6 个方程式由上述6 个边界条件得出:

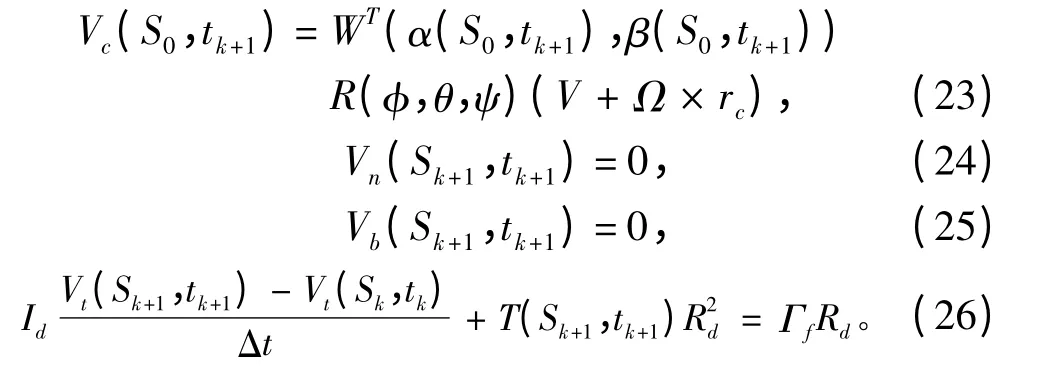
综合式(22)～式(26)，共可得到6(k+2)个非线性方程，其中k 可以求得。因此，对缆索的影响可以转化解这6(k+2)个方程的问题。由于这6(k+2)个方程都跟拖曳前行的时间有关，因此，在求解之前应该估算出拖曳的结束时间，这可以通过设定缆索的实际总长来实现。求tk+1时刻，缆索对航行器的影响，可以通过将tk+1代入式(12)和式(13)中进行求解得到。综上所述，数值法评估缆索对航行器影响的步骤如下:

1)设定边界条件。设定步长Δt和总时间T。设初始时刻tk=t0=0 时，缆索的浸水长度为0，航行器末端与滚筒端一致。于是，缆索的初始形态y(Sk，tk)可通过将t=0，航行器的初始状态参数(u，v，w，p，q，r，φ，θ，ψ)代入式(8)～式(11)来求解。

2)给出航行器tk+1=(k+1)Δt 时刻航行器的状态参数(u，v，w，p，q，r，φ，θ，ψ)。航行器每一时刻的状态参数可通过航行器上的传感机器来实时测量，或者通过航行器的动态模型来预测。

3)解非线性方程(22)～(26)。方程可通过Matlab 优化工具箱来进行求解。

4)求缆索的影响。将y(0，tk+1)及t=tk+1代入式(12)和式(13)。

5)k ←k+1。

6)若k ≤T/Δt 则回到步骤2，否则停止操作。

3 评估缆索对水下航行器的影响

水下航行器上缆索为细长，轻质等浮力缆索，连接在航行器的尾部，该连接点在航行器的动态坐标中表示为rc=(-0.5，0，0)。滚筒连接处缆索的张力可以忽略不计，即缆索枢轴与滚筒间滑动摩擦力产生的阻力矩Γf=0。缆索的相关参数及流体的相关参数如下:

ρ=1000，m=0.0049，A=4.9E－6，m1=0.0098，we=0，e=0，Ct=0.01，Cn=1.0，d=0.0025

3.1 缆索影响的评估

由于受到模型参数不精确的影响，水下航行器的动态模型有所误差。为了单独对缆索的影响进行评估，这里航行器自身的运动不做研究。由于水下航行器的控制包括前进速度、航向及航行器沉深3 个方面，为了简化计算，本文只考虑直航情况下，航行器水平直航情况:u=1，v=w=0，p=q=r=0，φ=θ=ψ=0。

图1 为直航时拖点处的张力变化图。从缆索拖曳力随时间近乎线性增长可以推断，当航行器的驱动力保持不变时，航行器将减速。换言之，要维持航行器匀速前移，驱动力必须相应增加。由于离散的偏微分方程无法用解析法进行求解，而用数值法解也并不容易。然而，上述情况中，将偏微分方程(7)与边界条件式(8)～式(11)联立时可以用解析法进行求解。缆索被航行器拖入静水中保持匀速纵荡时，必须在航行器运动方向上维持自身的形态。因此，缆索上的局部坐标系与惯性坐标系之间的方向角不随空间或时间的变化而变化:

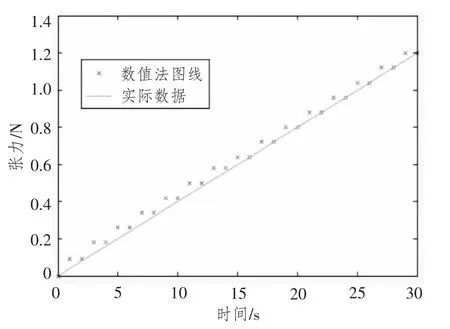
图1 航行器直航时缆索张力的变化情况Fig.1 Simulation results of cable drag under straight ahead motion

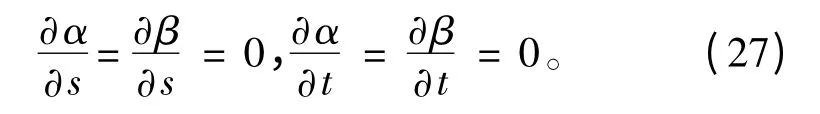
根据缆索局部坐标(τ，n，b)的定义，水平运动时方向角的大小为:

本文所研究的缆索为非弹性缆索，因此沿缆索方向的速度均为常数:

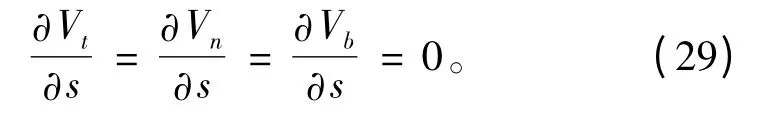
将式(28)和航行器相关运动参数代入边界条件(8)中，得到:

因此，缆索速度随时间的变化量也为0，即:

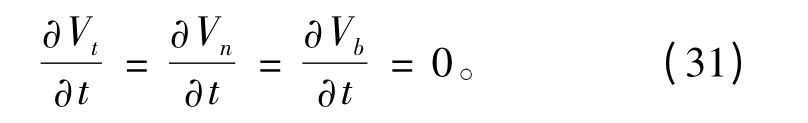
将式(27)～式(31)代入式(7)得到:

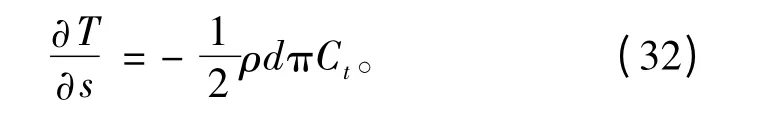
又由边界条件式(11)可得:

由式(32)和式(33)可得:

因此拖点处的张力为:

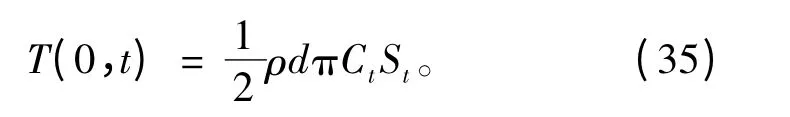
该式表明，拖点处缆索的张力与缆索浸水长度成正比。进一步分析，可以从式(14)得出:

综上所述，并结合缆索的相关参数，拖点处缆索的张力可以表示为:

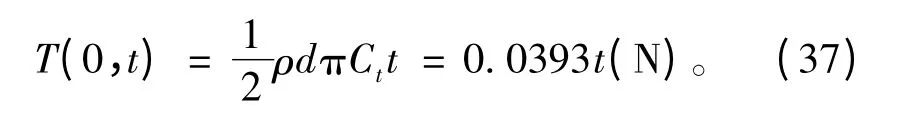
4 结 语

1)直航时拖曳处的缆索张力随时间的增加近乎线性增大，也即随着缆索长度的增加而增大;

2)可根据缆索拖点处所能承受的最大张力值，来指导拖曳距离或沉深，以避免拖曳过程中脐带缆索断裂;

3)随着拖曳时间的推移，若航行器的助推力保持不变，航行器将减速前移，而不能保持原来的匀速运动，因此，结论1)也可用以指导航行器助推力的变化;

4)在设计带缆航行器的自动驾驶装置时，应将缆索的影响考虑在内。这种设计，采用复合结构，包含1 个反馈路径和1 个前馈通路。其中，反馈控制器补偿无缆航行器的运动误差，而前馈控制器补偿缆索运动对水下航行器产生的影响。这使得无缆航行器的自动控制成为了可能，这种自动控制装置将是今后研究的重点。

［1］朱克强，李维扬．海洋缆体系统三维动态分析［C］．全国离岸工程学会论文集(上册)，1989:1－7．

［2］朱克强，曹奇英，施国庆．分段曳力系统在缆体系统仿真中的应用［J］．华东船舶工业学院学报，1993，7(1):18－24．

ZHU Ke-qiang，CAO Qing-ying，SHI Guo-qing．Appieation of seetional drag coeffieient to the cable 一body system modelin g［J］．Journal of Zhenjiang Zhipbuilding Institute，1993，7(1):18－24．

［3］施国庆，朱克强．水下缆控潜水器运动特性研究［J］．华东船舶工业学院学报，1993，7(3):1－9．

SHI Guo-qing，ZHU Ke-qiang．The motion characteristic analysis of tethered remotely operated driving vehicle［J］．Journal of East China Shipbuilding Institue，1993，7(3):1－9

［4］朱克强．舰舶与水下拖体系统耦合运动的非线性数值模拟［J］．华东船舶工业学院学报，1993，7(4)．

ZHU Ke-qiang．The nonlinear numerical simulation of ship and underwater towed body system coupling motion［J］．Journal of East China Shipbuilding Institue，1993，7(4):51－57．

［5］朱克强．水下遥控航行器的模拟与控制［J］．中外船舶科技，1994(4)．

［6］章浩燕，朱克强，张洋，等．水下拖曳缆索二维几何形态的研究［J］．舰船科学技术，2013，35(4):35－39．

ZHANG Hao-yan，ZHU Ke-qiang，ZHANG Yang，et al．Research on the two-dimensional cable geometries of a towed submersible［J］．Ship Science and Technology，2013，35(4):35－39．