海面浮动光电平台对空无源定位与跟踪

喻明阳，邱志强，陈 虹

(武汉第二船舶设计研究所，湖北 武汉430064)

0 引 言

无源定位技术是一种设备本身不发射信号，仅仅被动接受目标自身的辐射信息、角度信息或其他信息来实现定位的技术。与主动定位技术相比，无源定位技术无需自身发射探测信号，隐蔽性好、生存能力强，对提高系统的生存能力与作战能力具有重要作用。由于目标与观测站之间的距离信息是无源定位与跟踪的重要参数，被动测距问题是无源定位的关键问题。

光电被动测距技术主要有基于图像处理的测距法、基于角度测量的测距法、基于目标物体辐射特性和大气光谱传输特性的测距法等［1－2］。基于角度测量的几何测距法只需测量目标的角度信息以及观测站自身的位置信息，数据量小、数据测量与处理简单［3－4］，适合海面光电浮标的对空测距定位。为满足单站被动测距系统的可观测性要求，观测器与运动目标之间应该具备一定的相对机动条件［5－6］。与具有机动性能的飞机和舰船不同，自由漂浮在海面的光电浮标本身没有机动能力，不满足被动测距系统可观测的要求。由于海浪运动引起光电浮标在垂直于海平面的方向上产生一定的机动，使得高度固定的目标角度与角速度信息产生变化，达到系统可观测的要求。对目标和光电浮标的相对角度与角速度信息进行测量可以实现单站无源定位［7－8］。

为提高被动测距的精度，需对多次测量定位结果进行滤波处理。单站无源定位与跟踪系统的观测方程的严重非线性决定了定位与跟踪中必须采用非线性滤波技术。无迹卡尔曼滤波(Unscented Kalman Filter，UKF)通过构造一组确定的加权样本点经非线性变换来逼近高斯状态变量，避免对非线性观测模型的线性化，对任何非线性系统都可以精确到二阶，性能优于(Extent Kalman Filter，EKF)及其衍生算法。在单站无源测距定位的研究中，UKF 算法对系统进行滤波可提高测距精度［9－10］。

本文面向海上浮动光电平台对空中目标定位与跟踪，建立海上浮动光电平台对空中目标测距定位的数学模型，并引入无迹卡尔曼滤波进行存在噪声干扰的测距定位，通过仿真分析了基于UKF 的海上浮动光电平台对空测距定位的性能。

1 测距定位原理

假设在地球坐标系中，k 时刻光电观测平台的坐标:XO(k)=(xo(k)，yo(k)，zo(k));运动速度:运动加速度:AO=;k 时刻目标的坐标:XT(k)=(xT(k)，yT(k)，zT(k));运动速度:运动加速度:。

以海面浮动光电观测平台为坐标原点建立体坐标系，对空中目标定位建立如图1所示的数学模型。

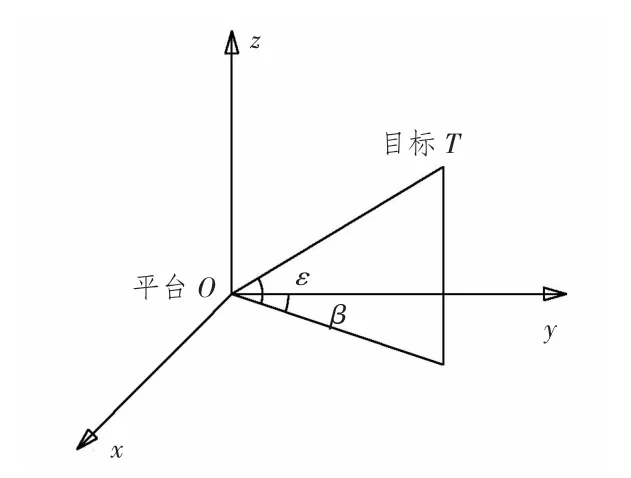
图1 无源定位系统示意图Fig.1 Illustration of passive location system

O－xyz 坐标系为浮动光电观测平台体坐标系，平台的正南方向为x 轴，正东方向为y 轴，垂直于海平面的上方向为z 轴。设k 时刻目标相对于观测平台的位置 X(k)=(x(k)，y(k)，z(k))，相对速度，相对加速度，其中X=XT－XO。目标相对于光电观测平台的方位角β，俯仰角ε 与径向距离r 都是时间k 的函数，β(k)，ε(k)，r(k)分别为:

联合式(1)～式(5)可得到2 个距离的求解公式:

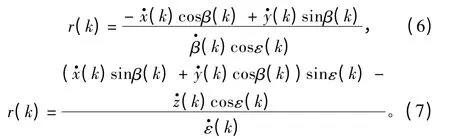
浮动光电平台搭载的红外光电探测系统能测量目标方位角β、俯仰角ε、方位角速度及俯仰角速度;观测平台自身的位置XO、速度VO与加速度AO信息由惯性导航系统测量给出。在目标固定不动的情况下，可以利用距离公式(6)或式(7)实现瞬时测距。

在多次测量的情况下，为提高测距精度，可以对数据进行滤波处理。将目标与浮动光电平台的相对运动设为状态变量，即则系统的非线性状态方程可描述为:

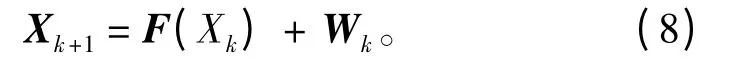
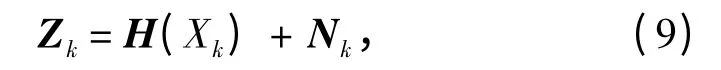
若系统过程噪声Wk和观测噪声Nk均为相互独立的零均值高斯白噪声，并且过程噪声方差阵Qk非负定，系统观测噪声方差阵Rk正定，根据系统给出的量测方程和状态方程，利用无迹卡尔曼滤波算法可提高测量精度和稳定性。根据给定的初值递推估计，从而确定目标的位置与运动状态。

2 无迹卡尔曼滤波

对于一个非线性离散系统:

具体的无迹卡尔曼滤波算法流程如下:

1)滤波初始化，k=0:

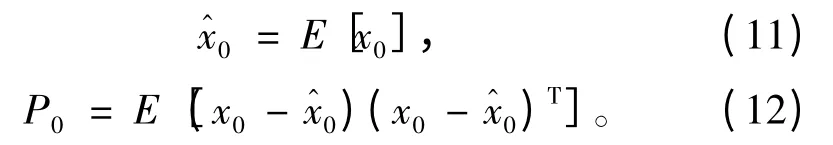
2)迭代过程，对于k=1，2…

①依据UT 变换计算2n+1 个Sigma 点:

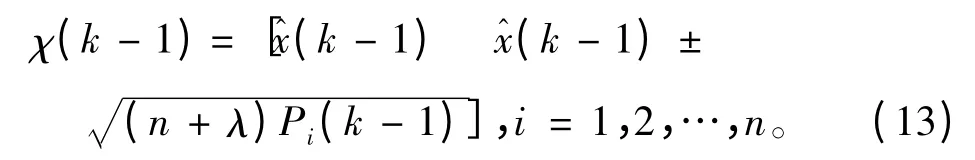
式中:λ 为比例参数，状态维数为n。

②时间更新

在得到Sigma 点集之后，将每个点代入系统方程得到变换后的Sigma 集:

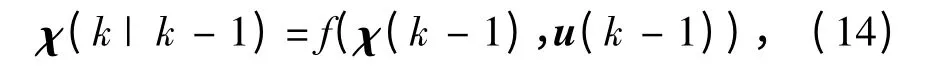
依据UT 变换规则，进行均值加权得到状态的预测均值:

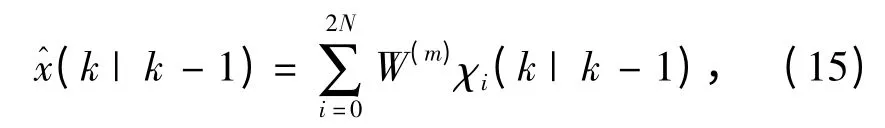
其中χi(k| k－1)涉及矩阵χ(k | k－1)的第i 列，i=0，1，…，2N。

依据UT 变换规则，进行协方差加权得到状态的预测方差:

再将每个变换后的Sigma 点利用观测方程进行非线性变换:

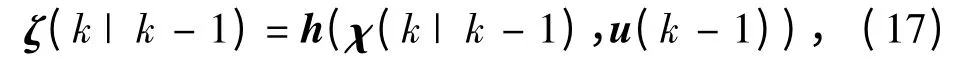
加权求和计算得到系统观测变量的预测值:

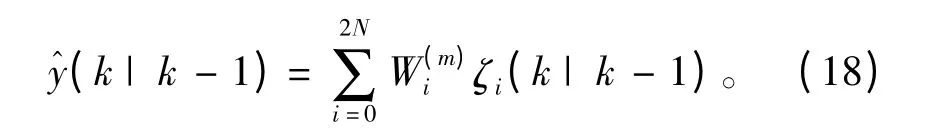
其中ζi(k| k－1)是矩阵ζ(k| k－1)的第i 列，i=0，1，…，2N。

③测量更新

计算更新的状态协方差:

计算互关联矩阵:

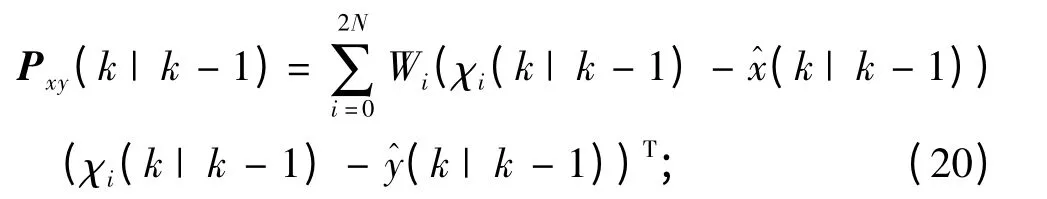
计算更新的Kalman 滤波反馈增益:

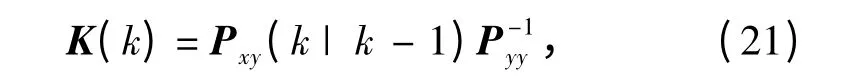
得到状态更新后的滤波值:

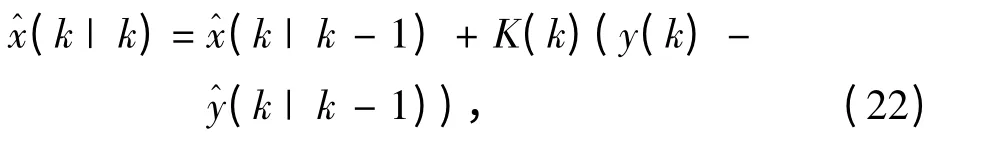
求解状态后验方差阵:

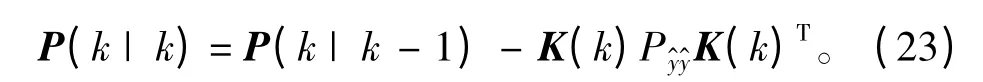
3 仿真过程

考虑海面上自由漂浮的光电平台对远距离低空固定目标或低速运动目标的测距定位。浮动光电平台在海面上的运动可分解为其在水平面上的运动与垂直水平面上的运动。在假设空中目标保持高度不变的情形下，由波浪引起光电平台在水平面上的运动对测距影响可忽略不计，在垂直海平面的方向上运动可视为准周期运动。故假设浮动光电平台在海面上随着海浪在垂直于海平面的方向上做正弦运动，忽略其在水平面上的运动。海面的海况等级以及相应海浪波高与周期等参见文献［11］。

假设光电观测平台测角的精度为0.18 mrad，测角速度的精度为0.1 mrad/s，每次测量的角度和角速度均含有零均值加性高斯噪声，方差与精度相同，测量周期T=1 s，观测次数N=100。光电观测平台在垂直水平面上做正弦运动，位置方差为0.1 m，速度方差为0.1 m/s;目标固定或在水平面上匀速航行，位置方差为10 m，速度方差为5 m/s。性能指标取距离绝对误差RE 来测度:

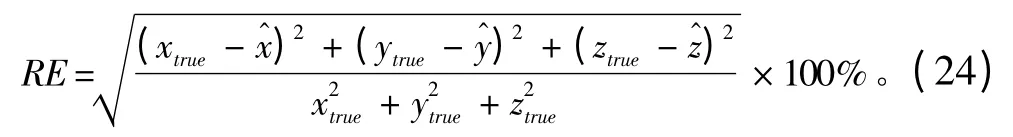
3.1 固定目标测距

仿真场景1:目标固定于(15 000 m，15 000 m，1 500 m)处，光电观测平台随着海浪在z 轴方向上做正弦运动。在3 级海况情况下，设光电观测平台运动周期为TO=4 s，振幅为SO=1.5 m;采用测距公式(7)计算固定目标的距离。

仿真场景2:目标固定于(15 000 m，15 000 m，1 500 m)处，光电观测平台随着海浪在z 轴方向上做正弦运动。在3 级海况情况下，设光电观测平台运动周期TO=4 s，振幅为SO=1.5 m;给定滤波初始值(20 000 m，20 000 m，1 480 m)，采用无迹卡尔曼滤波对多次测量的数据进行滤波估计。

图2(a)给出了固定目标的空间位置分量x，y，z轴的观测值与实际值曲线;从图2(b)可以看出，通过单次测量计算的距离与实际距离误差很大，距离的绝对误差曲线不收敛，幅值在0 ～1 之间波动。这是由于在远距离低空对空测距中，目标相对垂直高度远远小于相对水平距离、观测平台机做小幅正弦运动，使得俯仰角、俯仰角速度值与其测量误差都在10－4这个数量级上，距离估计对俯仰角速度的测量误差非常敏感。

图2 仿真场景1Fig.2 Scenario 1

图3(a)给出了固定目标的空间位置分量x，y，z轴的观测值、滤波值和真实值曲线，x 与y 轴的滤波曲线经过18 s 能收敛到真实值附近，z 轴则无法收敛，这是由于观测器在z 轴方向上的机动性不强造成的;图3(b)是UKF 距离估计曲线和距离误差曲线，估计距离误差在18 s 内可收敛到10%以内，体现了算法的滤波效果。

在目标固定不动、观测平台在z 轴方向上做正弦运动的情况下，由于对俯仰角速度的精度的异常敏感性，通过单次测量测距误差太大，单帧测距不可行;通过无迹卡尔曼滤波可以在18 s 内将估计误差减小到10%以内，提高测量俯仰角速度的精度可提高距离估计的精度。

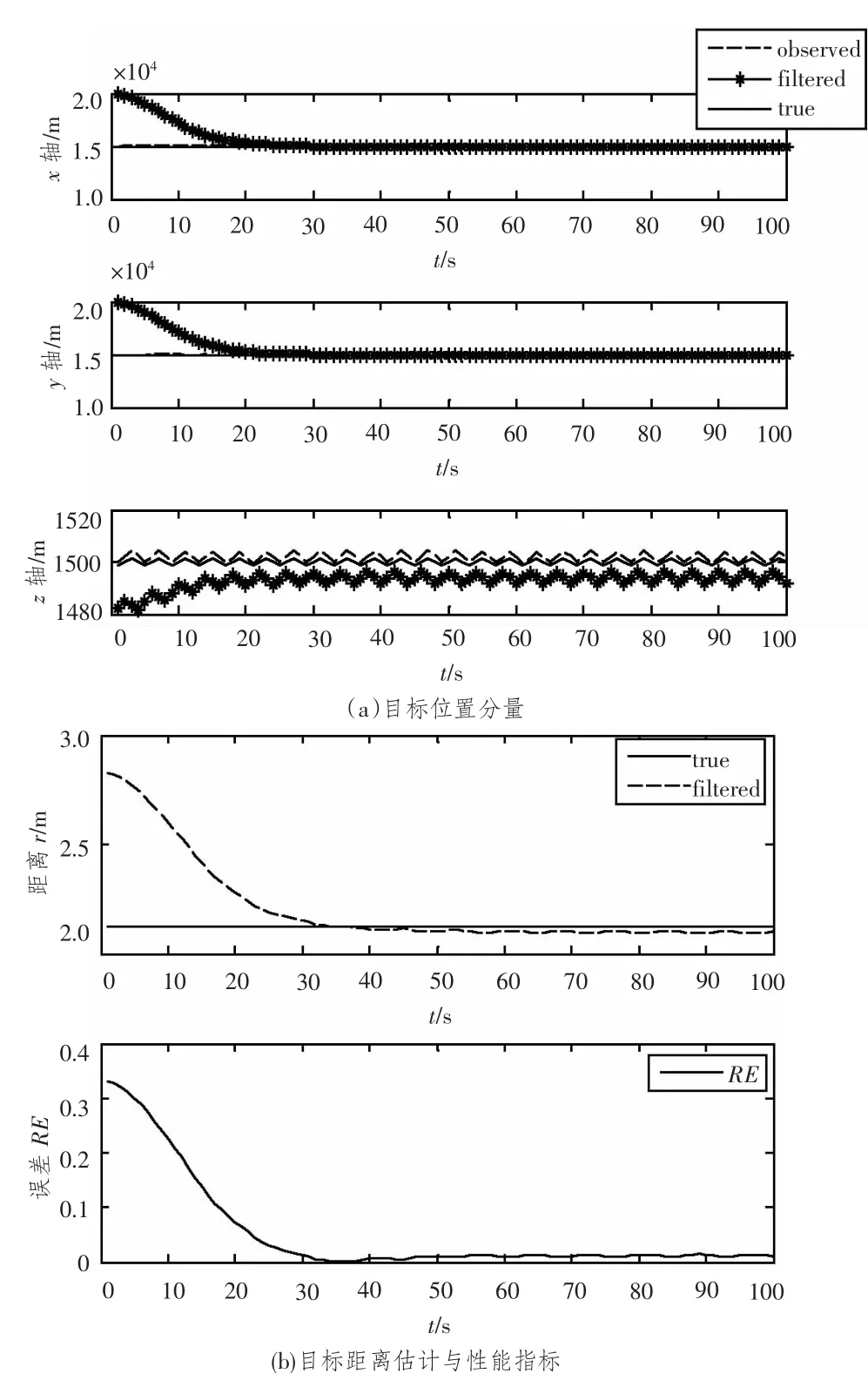
图3 仿真场景2Fig.3 Scenario 2

3.2 移动目标测距

仿真场景3:目标从(15 000 m，15 000 m，1 500 m)处出发，以速度(100 m/s，90 m/s，0 m/s)朝着观测平台作匀速直线运动，光电观测平台随着海浪在z轴方向上做正弦运动。在3 级海况情况下，设光电观测平台运动周期为TO=4 s，振幅为SO=1.5 m;采用无迹卡尔曼滤波对多次测量的数据进行滤波估计。

仿真场景4:目标从(15 000 m，15 000 m，1 500 m)处出发，以速度(100 m/s，90 m/s，0 m/s)朝着观测平台作匀速直线运动，光电观测平台随着海浪在z轴方向上做正弦运动。在6 级海况情况下，设光电观测平台运动周期TO=8 s，振幅为SO=5.5 m;采用无迹卡尔曼滤波对多次测量的数据进行滤波估计。

从图4(a)可以看出，UKF 估计对移动目标的位置空间分量x，y，z 的实际值进行了很好的跟踪，与图5(a)比较发现，观测平台振幅越大，z 轴上的跟踪效果越好，估计精度越高。

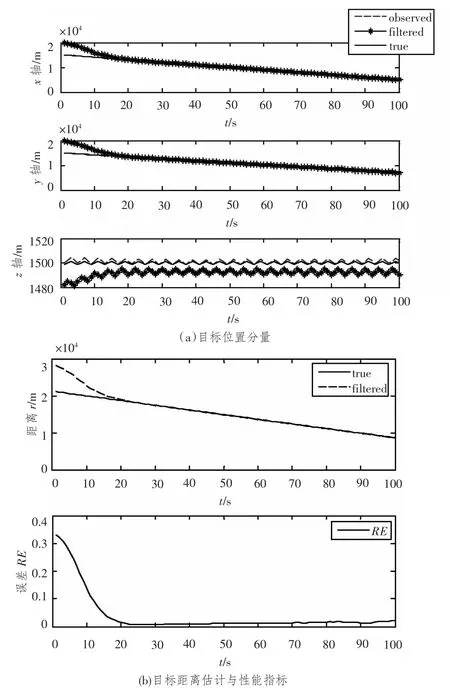
图4 仿真场景3Fig.4 Scenario 3

图4(b)与图5(b)给出了2 种海况情况下的距离估计曲线和误差曲线，估计的距离曲线能够很好地跟踪距离的理论值，而且距离绝对误差曲线随着时间的推移而收敛，估计距离误差在12 s 内可收敛到10%以内;从性能指标曲线的比较看出，2种情况下误差收敛的速度几乎一样。在6 级海况条件下，目标定位误差要较3 级海况小，提高观测平台在z 轴方向上的振幅可以有效减小定位误差和测距误差。

在目标移动、观测平台在z 轴方向上做正弦运动的情况下，UKF 可以有效提高距离估计的速度和精度;加强观测平台在z 轴方向上的机动性也可提高跟踪的精度。

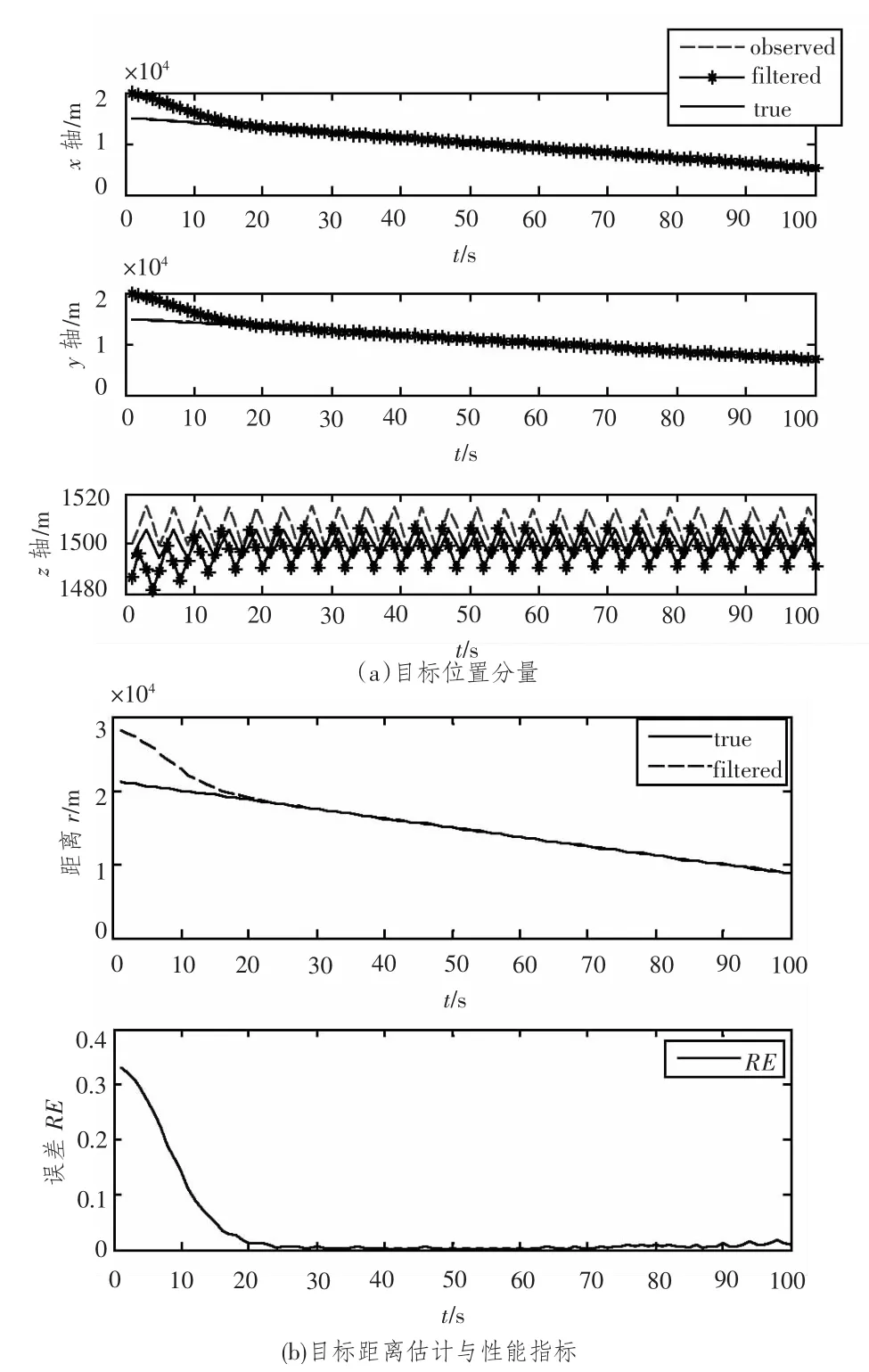
图5 仿真场景4Fig.5 Scenario 4

4 结 语

针对海对空的定位与跟踪问题，建立随着海浪运动的浮动光电观测平台对远距离低空目标测距定位的数学模型，利用UKF 算法估计目标的位置与速度信息，实现无源定位与跟踪。仿真结果表明，单帧测距的误差对俯仰角角速度非常敏感，对固定目标的测距误差较大;UKF 算法对目标跟踪定位效果好;在海浪峰值高的海况条件下，测距定位误差要小。另外，在后续的研究中，采用适当的手段，如在光电平台中内置冲击锤的方式短时增大光电观测平台在垂直海平面方向上的机动，有望提高测距定位的精度。

［1］陈友华，王丹凤，陈媛媛．光电被动测距技术进展与展望［J］．中北大学学报，2011，32(4):518－522．

CHEN You-hua，WANG Dan-feng，CHEN Yuan-yuan．Progress and prospect of optoelectronic techniques in passive range sensing［J］．Journal of North University of China(Nature Science Edition)，2011，32(4):518－522．

［2］冯国强，李站武，柳毅．简化UKF 在机载IRST 系统被动测距中的应用［J］．电光与控制，2012，19(2):63－67．

FENG Guo-qiang，LI Zhan-wu，LIU Yi．Application of simplified UKF in airborne IRST passive ranging［J］．Electronics Optics ＆ Control，2012，19(2):63－67．

［3］JOHNSON J A，FOWLER M L．Cramer-rao lower bound on doppler frequency of coherent pulse trains［A］．2008 IEEE International Conference on Acoustics，Speech and Signal Processing，ICASSP［C］．NJ，USA:Institute of Electrical and Electronics Engineers Inc．，2008．2557－2560．

［4］申波，朱斌，龙波，等．基于连续测角的被动测距技术研究［J］．电子设计工程，2010，18(12):45－48，53．

SHEN Bo，ZHU Bin，LONG Bo，et al．Research of passive measuring distance technique based on continuouslymeasuring angel［J］．Electronic Design Engineering，2010，18(12):45－48，53．

［5］郭福成，孙仲康．对机动辐射源单站无源定位的可观测性分析［J］．航天电子对抗，2005，21(3):31－33，53．

［6］王万平，魏宏刚，廖胜．被动测距的可观测性分析和滤波方法［J］．红外与激光工程，2009，38(6):1083－1088．

［7］ZHAN Rong-hui，WAN Jiang-wei．Iterated unscented kalman filter for passive target tracking［J］．IEEE Trans on AES，2007，43(3)．

［8］刘学，焦淑红．自适应迭代平方根UKF 的单站无源定位算法［J］．哈尔滨工程大学学报，2011，32(3):372－377．

LIU Xue，JIAO Shu-hong．Adaptive iterated SRUKF for singel oberver passive location［J］．Journal of Harbin Engineering University，2011，32(3):372－377．

［9］LEI M，HAN C．Sequential nonlinear tracking using UKF and raw range-rate measurements［J］．IEEE Trans．on AES，2007，43(1):239－250．

［10］司记伟，潘莉莉，刘嗥．基于平方根UKF 的机载单站无源定位跟踪算法［J］．舰船电子工程，2011，31(2):50－52．

SI Ji-wei，PAN Li-li，LIU Hao．Square-root UKF algorithm for singel airborne observer passive location and tracking［J］．Ship Electronic Engineering，2011，32(2):50－52．

［11］盛振邦，刘应中．船舶原理［M］．上海:上海交通大学出版社，2004:372－375．