复数辐角主值与反三角函数的关系及应用
盼刘铁
对于一些复杂的反三角函数问题,如果我们采用普通的三角方法,很难求解.但是,如果我们采用复数法,将反三角函数转化为复数的辐角主值再求解,既方便省事又简化了运算.
一、复数辐角主值与其他反三角函数的关系
z1=arctanyx;(-∞,+∞);(-π2,π2);
z2=arcsinyx2+y2;[-1,1];[-π2,π2].
z3=arccosxx2+y2;[-1,1];[0,π];
z4=arccotxy;(-∞,+∞);[0,π].
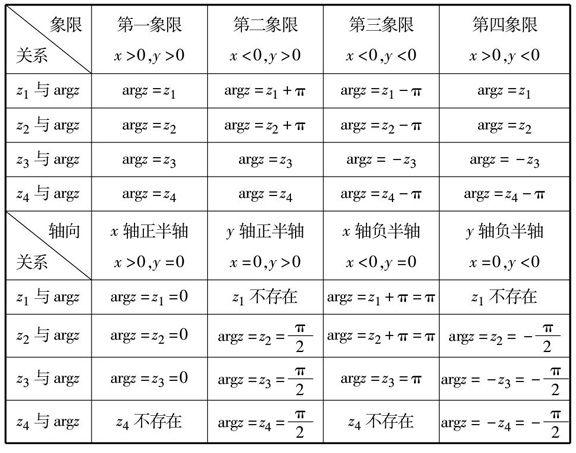
复数辐角主值与其他反三角函数的关系如下表:
象限
关系第一象限
x>0,y>0第二象限
x<0,y>0第三象限
x<0,y<0第四象限
x>0,y<0
z1与argzargz=z1argz=z1+πargz=z1-πargz=z1
z2与argzargz=z2argz=z2+πargz=z2-πargz=z2
z3与argzargz=z3argz=z3argz=-z3argz=-z3
z4与argzargz=z4argz=z4argz=z4-πargz=z4-π
轴向
关系x轴正半轴
x>0,y=0y轴正半轴
x=0,y>0x轴负半轴
x<0,y=0y轴负半轴
x=0,y<0
z1与argzargz=z1=0z1不存在argz=z1+π=πz1不存在
z2与argzargz=z2=0argz=z2=π2argz=z2+π=πargz=z2=-π2
z3与argzargz=z3=0argz=z3=π2argz=z3=πargz=-z3=-π2
z4与argzz4不存在argz=z4=π2z4不存在argz=-z4=-π2
二、应用
1.巧解反三角问题
例1计算arctanx+arctan1-x1+x(x<-1).
解:∵x<-1,1-x1+x=-1+21+x<-1,
∴-π2 ∴-π ∵arctan(-x)+arctanx-1x+1 =arg(1-xi)+arg[(x+1)+(x-1)i] =arg(1-xi)[(x+1)+(x-1)i] =arg[(x2+1)-(x2+1)i] =-π4. ∴arctanx+arctan1-x1+x=π4. 2.求角问题 例2若α,β为锐角,tanα=17,sinβ=110, 试证:α+2β=45°. 证明:∵α,β为锐角tanα=17,sinβ=110, 0<α<π6,0<β<π6,0<α+2β<π2, 又∵α+2β=arg[(7+i)(3+i)2] =arg(50+50i)=arg[502(cosπ4+isinπ4)], ∴α+2β=π4=45°. 3.求解反三角函数的证明题 例3已知a2+b2=c2, arcsin1a+arcsin1b=π2(a≠0且b≠0),求证:ab=c. 证明:∵arcsin1a+arcsin1b =arc(a2-1+i)+arg(b2-1+i) =arg[(a2-1)(b2-1)-1+(a2-1+b2-1)i] =π2. ∴(a2-1)(b2-1)=1,即a2b2=a2+b2. 又a2+b2=c2, ∴ab=c. 综上所述,在解决复杂的反三角问题时,如果不能直接求解,可将它转化为复数辐角问题,或可收到意想不到的效果. 参考文献 钟玉泉.复变函数论.北京:高等教育出版社,2013. 李中恢.复数法在三角问题中的应用.南昌:南昌高专学报,2008(4). 张建忠.复数辐角与反三角函数.甘肃:数学教学研究,1999(1). 李中恢.复数法在平面几何中的应用.宁波:宁波教育学院学报,2006(4).

