数学教学中培养初中生的学习技能
王德成
“教是为了不教”“授人以鱼,更要授人以渔”,这些都是教学活动的根本目的和要求.众所周知,教学活动不仅仅是为了传授学生深厚的学习“基石”,更重要的是教会学生认识问题、分析问题、解决问题的方法和技能.在以技能型人才为培养目标的今天,初中数学课堂教学的落脚点和归宿点应放置在学生学习技能的锻炼和培养上.教育实践学认为,学习技能培养是课堂教学的第一要务,也是有效教学的第一要义,应贯穿落实于整个课堂教学始终.基于以上认识,本人从三个方面就初中生数学学习技能在课堂教学中的培养进行简要论述.
一、点滴积累,重视初中生数学知识素养的培养
常言道,基础不牢,地动山摇.学习技能素养的有效提升和树立,需要良好的知识素养和深厚的知识根基作为支持和保证.教学实践证明,学习对象在感知、分析、解答问题过程中,借助于丰富的知识内容支撑,开展深入、高效的学习实践活动,才能实现学习技能素养的提升.因此,培养学习技能的首要条件和前提,就是要学习对象储备和积累深厚的知识内容,做好数学知识内容的传授和讲解工作.通过平时的点滴积累,树立起深厚的知识素养,为初中生学习技能提升打下坚实的“基石”.这就要求,教师在平时课堂教学活动中,要树立“积沙成塔,集腋成裘”的理念,将学习技能培养融入每一课堂之中,做好基础知识内容传授工作,针对每一节课的教学目标、教学重点、学习重点、认知薄弱点等方面,让学生在平时的点滴积累过程中,形成深厚、扎实的知识素养“功底”,为学习实践活动深入开展打下基础.
二、教授方法,提供初中生实践探究过程的指导
学习技能的培养,重点在学习方法的培养锻炼过程之中.学生学习技能素养的高低,可以通过解决问题的方法以及开展的学习实践活动进行展示和呈现.这就需要教师发挥自身所具有的主导特性,做好学习探究过程的指导和教学工作,既要为学习对象提供实践活动的舞台,又要为学习对象做好实践探究的指导,使学习对象对解决问题的方法策略能够有深入细致的理解和掌握.
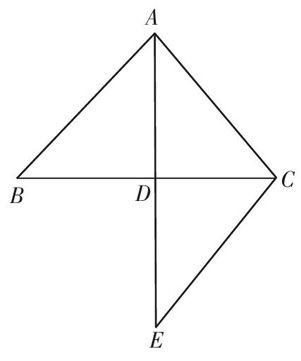
图1
例如,在讲“等腰三角形”时,等腰三角形三线合一是等腰三角形的重要性质和特征之一,同时也在该类型案例解答中应用广泛.教师可以围绕三线合一运用这一主题,开展案例教学活动,设置问题:如图1,在△ABC中,AD是∠BAC的角平分线,AD是BC边上的中线.求证:△ABC是等腰三角形.在探究分析问题条件过程中,学生认为要证明△ABC是等腰三角形,实际上就是要求证AB=AC.直接通过证明这两条线所在的三角形全等不行,此时初步得出该问题案例的解答思路“针对有中点的几何证明题,一般采用添辅助线的方法进行证明,可以通过‘延长加倍的形式,也就是延长AD到E点,使DE=AD,就能解决问题”.此时,教师根据学生的小组探究实践、思考分析思路,指出:通过对上述问题案例内容以及解题要求的分析,可以发现,在该问题解答过程中,需要利用借助于等腰三角形的三线合一这一知识点,构建问题条件与解题要求之间的“介质”.教师结合该问题案例引导学生共同探寻“三线合一”运用的方法策略.在实践探究过程中,学生结合典型问题案例,既掌握了数形结合解题策略的运用方法,又掌握了解决等腰三角形的一般方法,更提升了初中生学习知识、解决问题的技能和本领.
三、反思升华,注重初中生学习探知活动的评判
学习技能的养成过程,是一个不断前进、不断发展、不断反复的循序渐进过程.这一进程中,离不开教师的有效评价和学生的自主反思等双边活动.实践证明,学习对象学习技能的进步和提升,需要教师的有效“评”和学生的深刻“思”,并且二者之间相互融合,相互配合,共同作用.
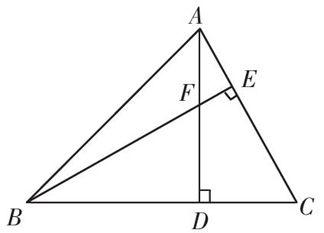
图2
例如,在讲“全等三角形的性质和判定”时,学生经常会出现审题不清,导致解题方法运用不科学的现象,教师可以设置问题:如图2,在△ABC中,∠ABC=45°,F是高AD和BE的交点,CD=4,则线段DF的长度为多少?并展示解题过程,组织学生围绕问题条件内容、解题思路、解题方法等方面的反思和分析活动,鼓励学生展示其解题观点,教师进行实时指导和补充,及时纠正学生解题方法及策略不足,帮助形成正确解题思路和方法,促进其数学学习技能素养的提升.
总之,在初中数学课堂教学中,教师应重视知识素养积累,强化学习活动指导,注重反思活动教学,为初中生良好学习素养树立打下基础.

