数学原理法分析种群的增长速率曲线和增长率曲线
张慕黎
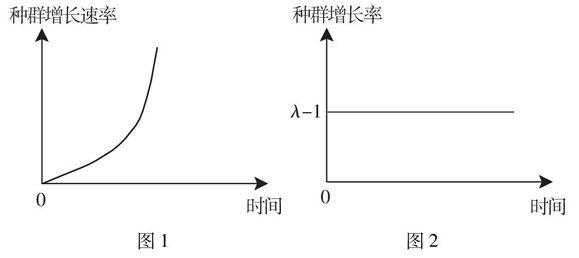
种群的增长方式包括 “J”型增长和“S”型增长,前者是在理想状态下,即资源、空间无限和不受其他生物制约的条件下产生的,后者是在现实状态下,即资源、空间有限和受其他生物制约的条件下产生的.
对于上述两种增长方式,区别种群增长率和增长速率的变化,到目前为止在中学生物教材和相应的教学辅导资料中还没有一个统一的说法,对此,笔者经过查阅资料和结合自己的教学实践略谈一二.
一、种群增长速率和增长率的定义
种群增长速率是指种群在单位时间内增加的个体数量,其计算公式为:增长速率=(现有个体数-原有个体数)/增长时间,单位可以用“个/年”表示.
种群增长率指种群在单位时间内净增加的个体数占原个体总数的比率.其计算公式为:增长率=(现有个体数-原有个体数)/(原有个体数·增长时间),单位可以用“个/个·年”表示.
二、指数增长的增长速率和增长率
种群在理想条件下呈指数增长,其增长曲线符合指数函数Nt=N0λt或Nt+1=Ntλ(N为种群个体数,N0为起始数,t为时间,λ为种群周限增长率,下同),其中λ具有开始和结束时间,它表示种群大小在开始和结束时的比率.
若以年为时间单位,指数增长种群的增长速率为:(N0λt+1-N0λt)个/年=N0λt(λ-1)个/年,所以指数增长种群的增长速率随时间变化呈等比数列,公比为λ,其通项公式为:dNdt= N0(λ-1)λt(dNdt表示种群增长速率).此通项公式是dNdt(相当于因变量)关于t(相当于自变量)的指数函数,其变化过程如图2.
图1图2
以年为时间单位,指数增长种群的增长率为:(Nt+1-Nt)个/Nt个·年=(N0λt+1-N0λt)个/N0λt个·年=N0λt(λ-1)个/N0λt个·年=(λ-1)个/个·年,即该种群在一年时间内平均每个个体增加的个体数为λ-1个.因为λ-1为常数,所以指数增长种群的增长率曲线与x轴平行,且在y轴上的截距为λ-1,如图2.
三、逻辑斯谛增长的增长速率和增长率
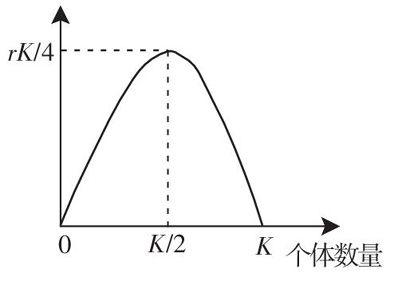
种群在自然条件下呈逻辑斯谛增长,逻辑斯谛增长曲线(“S”型曲线)是根据逻辑斯谛方程构建的曲线模型.逻辑斯谛方程的数学表达式为:dNdt=rN(K-NK)(r是瞬时增长率,K是环境容纳量,特定种群的r和K都为定值).此方程是dNdt(相当于因变量)关于N(相当于自变量)的二次函数,坐标曲线为抛物线,其特征为:①开口方向:二次项系数为-rK,曲线开口向下;②存在最大值:当N=K2时,dNdt=rK4为种群的最大增长速率;
图3
③与横坐标的交点:当N=0或N=K时,rN(K-NK)=0,故曲线与横坐标的交点为N=0和N=K;④对称性:以N=K2为对称轴两侧对称(如图3).
图3常被各种教辅资料引用,但在引用时,常将横坐标名称个体数量改为时间,使曲线的科学性出现偏差.
探讨逻辑斯谛增长种群的增长速率和增长率随时间变化的情况,需对逻辑斯谛方程进行积分,得Nt关于t的函数式:Nt=K1+KN0-1en
(特定种群的N0为定值).
分析图3,推知逻辑斯谛增长种群的增长速率曲线为钟形曲线.有以下特征:①存在一个最大值;②在最大值之前,种群增长速率逐渐增大,增大的过程遵循“慢→快→慢”的“S”型变化规律;③在最大值之后,种群增长速率逐渐减小,减小的过程遵循“慢→快→慢”的反“S”型变化规律.
逻辑斯谛增长种群的增长率曲线为“反S”型曲线.其特征为:种群增长率一直减小,减小的过程遵循“慢→快→慢”的变化规律.
总之,曲线模型在中学生物教学中的应用很广泛.在曲线模型构建中,我们不能主观随意作图,更不能混淆概念间的关系,尤其不能随意改动和更换横纵坐标的含义,需要运用数学形式来描述生物学系统的变化趋势,并进行模型的检验,最终形成一个较为准确的曲线模型.

