冷轧卷取机中空轴损坏原因分析与改进

贺战马，强艳丽

(中冶陕压重工设备有限公司，陕西 富平 710119)

0 前言

普碳钢带材单机架、双机架可逆冷轧机组的张力卷取机卷筒常用四棱锥轴式结构。生产中卷筒上的中空轴法兰豁口经常产生开裂，导致中空轴损坏。更换中空轴必须拆除卷取机上的压辊装置、推板装置、涨缩油缸及回转接头，并打开张力卷取机的传动箱箱盖，拆卸中空轴上的大齿轮及其两端的卷筒轴承，将卷筒的四棱锥轴从中空轴中抽出。因此，拆卸和装配的操作过程繁琐，影响带钢的轧制生产效率。

中空轴为合金钢锻件，结构为细长型空心薄壁圆筒，端部为带豁口的法兰式形状，热处理工艺复杂，锻造和机械制造难度大，成品率低，成本造价很高。因此，本文分析中空轴法兰豁口开裂损坏的原因，计算其受力变形产生角位移，提出改进结构设计的方案，以解决中空轴法兰豁口开裂损坏问题，有效地提高轧机的正常生产时间。

1 卷取机卷筒结构及参数

1.1 卷筒结构及组成

某1 150 mm单机架六辊可逆冷轧机的张力卷取机卷筒的结构如图1所示。卷筒安装在卷取机箱体内，其主要由中空轴9、四棱锥轴2、卷筒端部支撑头1、四块扇形板3、滑块4(安装在扇形板上)等组成。卷筒传递卷取扭矩的过程:箱体内的大齿轮通过双键驱动中空轴转动，中空轴通过右侧的双键驱动四棱锥轴转动，四棱锥轴通过四棱锥及滑键带动四块扇形板转动从而使卷筒产生卷取带材的张力。

1.2 卷取机力能参数

卷筒直径/mm φ510(正圆)

卷筒涨缩范围 mm φ510～φ495

带卷直径mm φ510 ～φ1 900

钳口开口度/mm 10

卷取张力/kN 140～14 (v＜495 m/min)80～8 (v≥495 m/min)

最大卷取速度/m·min－1768

卷取电机 Z560～4B

功率/kW 790×2

电压/V 660

转速/r·min－1406/1 200

速比 i总1=3.884，i总2=2.503

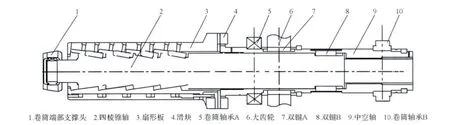
图1 卷筒装配示意图Fig.1 Schematic of the reel assembly

2 中空轴结构及故障分析

如图2所示，安装在扇形板端部上的滑块呈“凸”字形状，位于滑槽内，沿着中空轴左端法兰盘上的滑槽豁口，随着扇形板涨缩沿滑槽作径向滑动，主要起到扇形板轴向定位的作用，不应承受或轻负载承受卷取带材的扭矩。但是，在传动过程中，中空轴、四棱锥轴产生的扭转变形较大时，扭转变形量超过滑块与滑槽之间的单边隙时，滑块就形同一个传动滑键，按照传动方向朝着滑槽豁口施加推力，直接驱动扇形板旋转，而且中空轴与四棱锥轴间的双键则大大减少了所传递的扭矩，而滑槽豁口在机械强度和结构形状上属于薄弱环节，难以承受较大的扭矩载荷。

图3为中空轴的剖面图和法兰端面图。

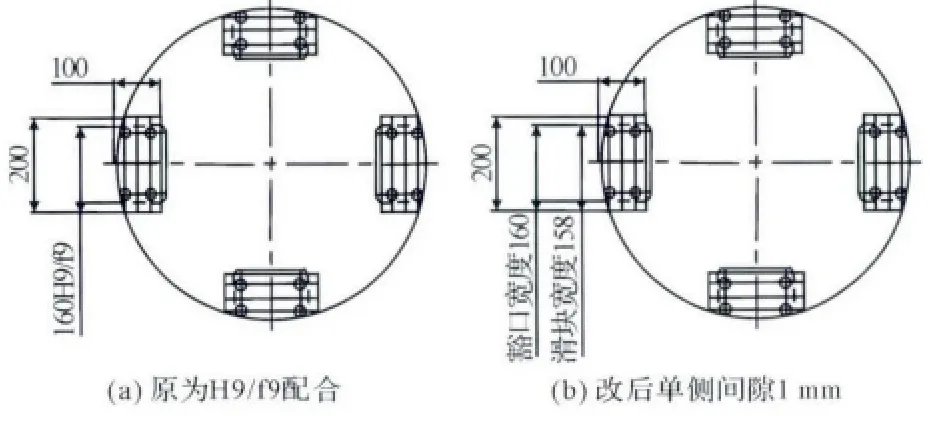
图2 改进前后滑块与豁口的间隙Fig.2 Gap around the slider and the notch

图3 中空轴结构简图Fig.3 Structure diagram of the hollow shaft

3 卷筒受力分析及计算

在实际工作情况下，零件在受力时都会产生弹性变形，中空轴和四棱锥轴因受力变形产生角位移。卷筒所受扭矩最大扭矩是按卷取最大张力乘以带材卷最大卷径得出的。即

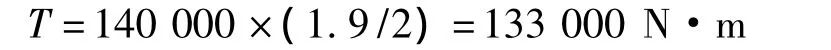
3.1 中空轴扭转角位移计算

中空轴受大齿轮作用的主动扭矩T，同时受四棱锥轴作用的从动扭矩T，这两个扭矩大小相等，方向相反，形成一对外力偶矩Me。

假设中空轴材料符合胡克定律，剪切模量G=80 MPa，计算中将中空轴近似视为壁厚均匀的等直空心圆截面杆，外径为D=0.397 m，内径为d=0.322 m，中空轴两力矩间距离为L1=0.45 m，如图4所示。当等直空心圆截面杆仅在两端受一对外力偶作用时，则所有截面上的扭矩T均相同，且等于杆端的外力偶矩Me。外力偶矩Me=T。此外，对于用同一材料制成的的等直空心圆截面杆，G和Ip亦为常量。于是，中空轴旋转时两扭矩作用的两个横截面绕中空轴轴线转动的。

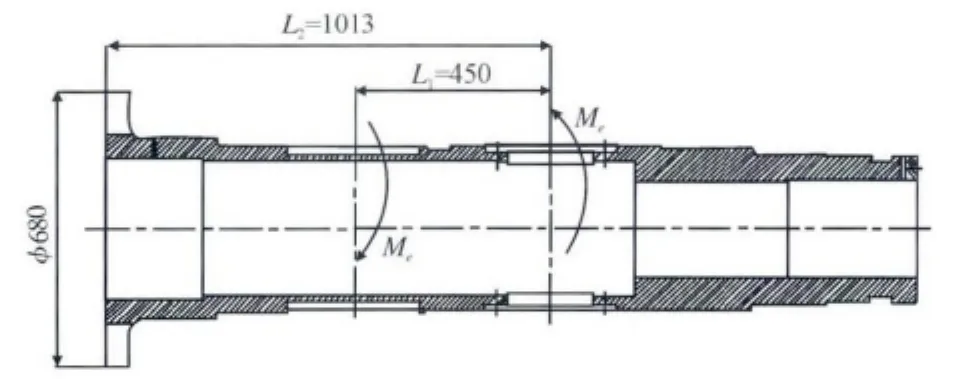
图4 中空轴受力图Fig.4 Force diagram of hollow shaft

相对角位移即相对扭转角φ1为

法兰豁口处产生的相对扭转角φ2为

法兰豁口φ680处产生周向变形位移为

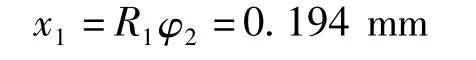
式中，R1为法兰豁口半径，R1=340 mm。

因此，中空轴在一对外力偶的作用下，法兰豁口φ680处的圆周方向上产生有0.194 mm的变形位移。

3.2 四棱锥轴扭转角位移计算

四棱锥轴与中空轴类似，受两个扭矩大小相等，方向相反，形成一对外力偶矩Me。由于四棱锥轴为不规则形状，一段近似为实心圆柱形，一段近似为四棱锥轴形，如图5所示。于是将四棱锥视为一段等圆截面的圆柱形和一段等四棱锥截面的非等圆截面的四棱锥形，分别进行扭转角位移计算。

(1)圆柱形段扭转角位移计算。四棱锥轴实心圆柱直径为d=320 mm，则四棱锥轴圆柱形段绕中心轴的相对扭转角位移φ3为

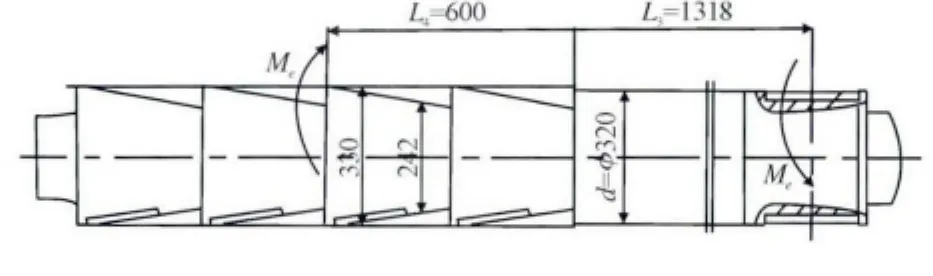
图5 四棱锥轴结构Fig.5 Structure diagram of quarto-prism mandrels

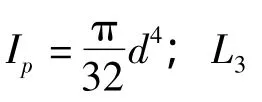
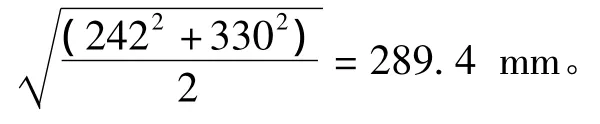
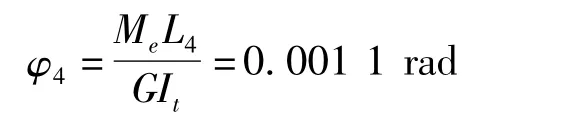
式中，It为截面的相当极惯性矩，It=αb4;L4为四棱锥轴两扭矩之间的四棱锥段长度，取卷筒筒身中间位置到圆柱L4=0.6 m。

α可查表得出，其值随矩形截面的长、短边尺寸h和b的比值m=h/b而变化。由于四棱锥轴的等效截面为正方形，所以m=1，通过查表得 α=0.140。

扇形板最大直径端(也就是滑块)的扭转角位移为

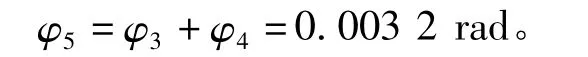
滑块产生周向变形位移为

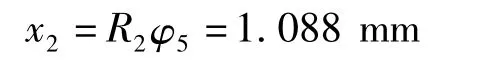
式中，R2为滑块最大外轮廓半径，R2=340 mm。

四棱锥轴反映到滑块处的角变形产生的周向变形位移为x2=1.088 mm。

(3)中空轴法兰豁口与滑块间扭转变形的总值。中空轴法兰豁口与滑块间扭转变形总值应该是中空轴扭转角位移、四棱锥轴圆柱形段扭转角位移和四棱锥轴四棱锥形段扭转角位移之和。即

4 中空轴豁口与扇形板的角位移差

中空轴法兰豁口与扇形板滑块之间的角位移差值主要由从卷筒驱动用大齿轮双键、中空轴驱动四棱锥轴用双键、四棱锥轴拖动扇形板用滑键、扇形板上安装的滑块与中空轴法兰豁口之间产生的机械制造间隙构成角位移差。

由零部件图纸知:齿轮箱中大齿轮、双键和中空轴之间为过盈配合，因此没有间隙;中空轴、键和四棱锥轴之间配合为70D10/f9、70H9/f 9，四棱锥轴、键和扇形板三者之间配合为40N9/h9、40H11/h9;因此，由中空轴到四棱锥轴、扇形板之间所有配合的累计最大间隙为0.546 mm，最小间隙为0.222 mm。其平均间隙值为0.384 mm;该平均间隙值基本上处在φ322～φ397 mm之间，反映到φ680 mm滑块处时可产生平均值为0.725 mm的位移。扇形板端部与滑块之间的配合为160H9/f9，最大间隙为0.243 mm，最小间隙为0.043 mm，平均间隙值为0.143 mm。因此，所有机械配合间隙最终反映到中空轴法兰滑槽内的滑块处，可形成平均间隙为0.725－0.143=0.582 mm。

本文不考虑各个键及滑键、滑槽挤压变形产生的间隙值。则中空轴法兰豁口与扇形板滑块之间的角位移差值总和实际上等于:∑=0.582+δ+1.282=1.864+δmm。

扇形板滑块与中空轴法兰豁口之间原设计间隙配合160H9/f9，最大间隙远远小于总和角位移差值(1.864+δmm)，导致扭矩传递直接由中空轴传递给法兰豁口内的滑块，滑块再拖动扇形板旋转，在最大张力的扭矩作用下，法兰豁口中的滑块将法兰豁口底部有劈裂的趋势，本应主要承担传递扭矩的四棱锥轴反倒承载很小。

5 改进措施

扭矩的分配与滑块和豁口间的间隙值紧密相关，合理地将总传递扭矩分配到四棱锥轴传递和中空轴法兰传递。将法兰豁口与滑块之间的间隙按照上述计算值∑予以适当增大的设定，让滑块主要起到在轴线方向上使扇形板定位，不承受张力卷取的扭矩或者在产生一定的扭转变形后滑块与中空轴法兰豁口压紧，适当承受少量扭矩不至于将法兰豁口劈开，且能够在滑槽内灵活滑动。因此，滑块与中空轴法兰滑槽间的单侧间隙应设定为1.0～1.5 mm较为宜。一般轧制情况下，卷径、张力都不在最大值时，扭矩靠双键传递，滑块与法兰豁口无需扭矩传递;卷径、张力都处在最大值附近时，大量扭矩通过双键经四棱锥轴传递给扇形板，少量扭矩通过法兰豁口内的滑块传递给扇形板，避免了中空轴法兰豁口的开裂。

6 结束语

通过计算传递扭矩环节的角位移和机械间隙等总体形成的错位值，进而增大中空轴法兰豁口与滑块间的间隙，避免滑块受传动扭矩，改善了中空轴法兰的受力状况，防止了中空轴的损坏，延长了使用寿命。

［1］周国盈编著.带钢卷取设备(2版)［M］.北京:冶金工业出版社，1992.

［2］高新建，唐迪龙.四联冷轧带钢卷取机油缸和回转接头的改造［J］.新疆钢铁，2003(2).

［3］孙训方等编著.材料力学(Ⅰ)(1版)［M］.北京:高等教育出版社，2002.

［4］邹家祥.轧钢机械理论与结构设计［M］.北京:冶金工业出版社，1993.

［5］邹家祥.轧钢机械［M］.北京:冶金工业出版社，1989.

［6］黄庆学主编，轧钢机械设计［M］.北京:冶金工业出版社，2007.

［7］王廷傅刘克敏主编.金属塑性加工学－轧制理论与工艺［M］.北京:冶金工业出版社，2001.

［8］曹宏德.塑性变形力学基础与轧制原理［M］.北京:机械工业出版社，1979.