基于正交预编码的线性分散空时频编码

(杭州电子科技大学通信工程学院，浙江 杭州310018)

0 引 言

空时频编码技术在MIMO-OFDM系统中扮演着重要的角色。正交空时频编码[1]和准正交空时频编码[2]均是以牺牲频谱利用率为代价来换取最大的分集增益。分层空时编码[3]是以牺牲部分分集增益的代价来获得较高的频谱利用率。文献[4]引出了线性分散码的概念，该编码方案是同时考虑复用和分集来设计的，以期达到较好的性能。文献[5]针对准静态瑞利衰落信道，提出了一种适合整个信噪比区间的线性分散码设计准则。文献[6]在文献[4]的基础上提出一种非方阵结构的线性分散编码方案，且可获得与文献[4]相同的码率，同时将其应用于快衰落信道中。文献[7]将线性分散码应用于单载波频率域均衡系统，获得了良好的分集和复用增益。针对MIMO-OFDM系统中现有的线性分散空时码编解码复杂度高的问题，文献[8]提出了一类正交线性分散码，在获得满空时分集增益的同时，大大简化了系统的编解码复杂度，但其并没有获得良好的频率分集增益。文献[9]在接收端采用简单的检测算法，设计出一种在相关瑞利衰落信道下能获得满码率的线性分散编码方案。本文利用正交预编码[10]的方法，结合正交线性分散码，获得空时分集增益和频率分集增益良好的折中，仿真结果证明，本文提出的方法能够使系统的误比特性能得到明显的提高。

1 系统模型

在一个具有Nt副发送天线，Nr副接收天线的MIMO-OFDM系统中，设信道具有频率选择性，多径数为L+1，OFDM 子载波个数为Nc，且发射天线i 到接收天线j 之间的信道信息的时域脉冲响应可表示为:

式中，Τ代表转置，hj，i各系数为服从零均值、方差均为1/(L+1)的高斯分布的随机向量，则其频率响应为:

式中，p=1，…，Nc，j=1，…，Nr，i=1，…，Nt，Hj，i(p)为子载波p 上发送天线i与接收天线j 之间的频率响应。设在第n个OFDM 符号周期的第p个子载波上发送的M×Nt维的空时码字为Cp，M为每个码字的持续时间，则Nr根接收天线上的信号为:

W(p)为第p个子载波上的噪声矩阵，其维数为M×Nr，空时编码采用线性分散编码，其在子载波p上对应的编码矩阵Cp定义为一组M×Nt维的复基矩阵的线性组合，而权系数为子载波p 上的K个发送数据符号因此可见Cp完全由复基矩阵决定。将Cp代入式(3)，可得:

2 正交线性分散码

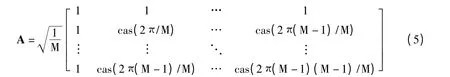
式中，cas(θ)=cos(θ)+sin(θ)，不难得到AΗA=IM，(·)Η为求矩阵的共轭转置，定义Φk为矩阵A的第(k-1)Nt+1列到第2(k-1)Nt列所组成的M×Nt维矩阵，其中k=1，2，…，K，M=K×Nt，从而证明:

3 正交预编码

正交预编码利用相互正交的矩阵CNt和DNt，分别对发送信号的实部和虚部进行编码，组合成复信号ENt即可得到ENt=CNtU+jDNtV。其中U =real(X)，V =imag(X)分别表示X的实部和虚部，CNt和DNt可表示为其中本文中有Q =Nc。关于以上CNt和DNt的具体推导过程，详见文献[10]。设经过星座调制后有K×N个输入符号，定义这K×N个输入符号为对X的每一行Xk(k =1，2，…，K)分别进行正交预编码后得到符号矩阵分别选取矩阵E中的第p(p =1，2，…，Nc)列Ep作为子载波p 上的K个发送信号序列，则通过线性分散编码后得到第p个子载波上发送的符号码字矩阵为

4 接收端解码

由前面的分析可知，在经过正交预编码后，接收端符号在子载波p 上可表示为:

对式(7)两边做按列拉直运算vec(·)，得到y(p)=G(p)Ep+n(p)。其中等效信道矩阵可表示为其中，hu(p)(u =1，2，…，Nr)是信道矩阵H(p)的第u列，y(p)=vec(Y(p))，n(p)=vec(W(p))。根据MMSE 准则可以推导得到权值系数为求矩阵的逆，σ2表示接收平均信噪比，获得权值ω(p)后，得到对Ep的判决估计从而可得到根据正交预编码的逆过程，得到其中和分别表示矩阵X和E的第k 行的判决估计值，从而可对输入符号作出判决。

5 性能仿真与分析

仿真参数如下:

1)子载波数Nc=128;

2)信道为频率选择性信道，但在时间上是平坦的，实现次数为counter=1 000次，多径数L+1 =5;

3)FFT点数为Nc，循环前缀CP的长度为FFT 长度的1/4，调制方式为QPSK。

仿真1 本文提出的方法在发收天线数分别为(2，1)，(2，2)，(3，1)，(3，2)下的性能比较，仿真结果如图1所示。

从图1可以看出，随着接收天线数的增加，系统的性能也在不断的增强，在误比特率为10-3时，2发2收比2发1收能获得接近4.5 dB的增益，3发2收比3发1收获得4 dB的增益。

仿真2 对基于正交预编码的线性分散空时频编码与文献[8]中提出的方法及正交预编码的方法进行了性能比较，仿真结果如图2所示。

从图2可以看出本文提出的结合正交预编码的线性分散编码比文献8中的方法在大信噪比的情况下有着明显的性能提高，在误比特率为10-3时，能获得近2 dB的性能增益。

图1 不同天线数配置下的性能曲线

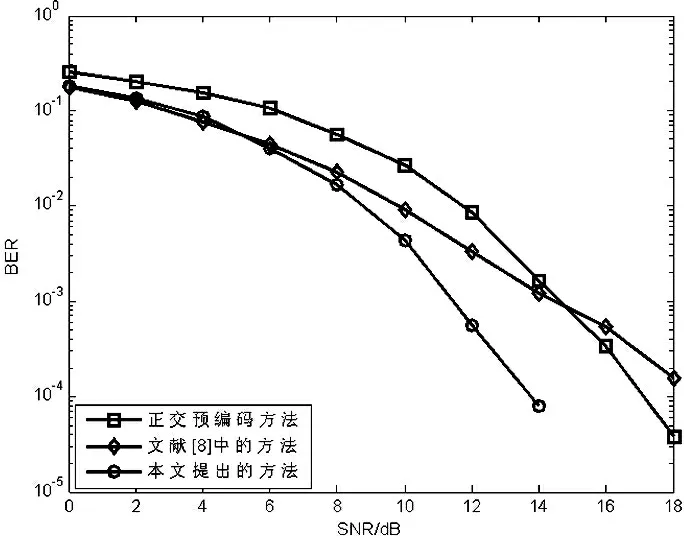
图2 不同编码方式下的性能曲线

6 结束语

本文利用正交预编码具有良好的频率分集优势，结合可获得满空时分集增益的线性分散码，提出了一种新的空时频编码方法，从而使系统的误比特性能得到了明显的提高，且编解码复杂度较低。

[1]Alamouti S M.A simple transmit diversity technique for wireless communications[J].Selected Areas in Communications，IEEE Journal on，1998，16(8):1 451-1 458.

[2]Su W，Xia X G.Signal constellations for quasi-orthogonal space-time block codes with full diversity[J].Information Theory，IEEE Transactions on，2004，50(10):2 331-2 347.

[3]El Gamal H，Hammons A R.A new approach to layered space-time coding and signal processing[J].Information Theory，IEEE Transactions on，2001，47(6):2 321-2 334.

[4]Hassibi B，Hochwald B M.High-rate codes that are linear in space and time[J].Information Theory，IEEE Transactions on，2002，48(7):1 804-1 824.

[5]范忠亮，王永生，许家栋，等.MIMO系统中线性分散码的设计准则[J].西北工业大学学报，2010，28(2):245-248.

[6]Wu J，Blostein S D.Rectangular information lossless linear dispersion codes[J].Wireless Communications，IEEE Transactions on，2010，9(2):517-522.

[7]Marchetti，N，Cianca E，Prasad R.Space-frequency linear dispersion codes for single carrier-frequency domain equalization[J].Wireless Communications，IEEE Transactions on，2009，8(11):5 388-5 393.

[8]王磊，朱世华，王君.可获得满分集增益的正交线性分散空时编码[J].西安交通大学学报，2005，39(8):852-855.

[9]Kuhestani A，Azmi P.Design of efficient full-rate linear dispersion space-time block codes over correlated fading channels[J].IET Communications，2013，7(12):1 243-1 253.

[10]Park，S S，Kim H K，Baik H K.A simple STF-OFDM transmission scheme with maximum frequency diversity gain[J].Proceedings of the 2004 International Symposium(ISCAS'04)，2004，4(4):101-104.