N=2超代数的一类子代数的研究

党佳华，刘 东，高寿兰

(1.杭州电子科技大学理学院，浙江 杭州310018;2.湖州师范学院理学院，浙江 湖州313000)

0 引 言

N=2超共行代数是数学物理中一类重要的研究对象。截止目前为止，N =2超共行代数中仍有许多问题值得进一步研究，特别是其表示的分类问题仍是一个公开的难题，许多论文给出了特殊结论和各种猜想。文献[1]刻画了N=2超共行代数;文献[2]讨论了阶化线性空间和李超代数的基本性质，给出了经典李超代数的分类及基本经典李超代数的Kac-Dynkin 图，特别是介绍了如何运用广义的不可约张量算符及Wiger-Eckart 定理，求经典李超代数不可约表示的方法;文献[3]介绍了有限维李代数的中心扩张和导子代数;本文对复数域上基为Lm，Mm，Gp的李超代数N的结构性质进行讨论并给出相关结论。

1 预备知识

本文主要讨论了李超代数N的2-上同调群，导子代数，自同构群等结构问题。在本文中，令S*表示任意集合S的非零元素集合，分别用C，Z 来表示复数集和整数集。

2 泛中心扩张

李超代数N 上的二上循环是复数域C 上双线性函数ψ:N×N →C，并且有ψ(x1，x2)=对任意的

记N的二上循环和二上边界的线性空间分别为A2(N，C)，B2(N，C)。定义N的二阶上同调群为商空间H2(N，C)=A2(N，C)/B2(N，C)。

定理1 dimH2(N，C)=3，其中关于N的常见的不平凡二上循环如下φ(Mm，Mn)=mδm+n，0C2，φ(Lm，Mn)=m(m-1)δm+n，0C3，φ(Lm，Gp)=φ(Mm，Gp)=φ(Gp，Gr)=0，对任意的成立。

3 李超代数N的导子

令V是一个N-模。从N 到V的线性映射φ 叫做导子，如果对任意的x，y∈N，有φ[x，y]=xφ(y)-yφ(y)。当v∈V，映射φ:x→x·v 称做内导子，用Der(N，V)和Ιnn(N，V)分别表示所有导子和内导子的向量空间。定义V中的N的一阶上同调群为:H1(N，V)=DerC(N，V)/InnC(N，V)[3]。

定理2 Der(N)=ad(N)。

证明 对任意的D∈Der(N，V)0，设D(Ln)=(a(n+1)-bn)Mn，D(Mn)=cMn。这里任意的n∈Z，a，b，c∈C[4]。对任意的设D(Gr)=CrGr，其中Cr∈C。将D 作用到[M0，Gr]=Gr，得到c=0和Cr=C1，其中C1∈C*。那么D(Gr)= C1Gr。将D 作用到[L0，Gr]= rGr上，得aGr+rC1Gr=rC1Gr，比较系数得知a=0。将D 作用到上，得b =0。D(Ln)=0，D(Mn)=0，D(Gr)=C1Gr。令D0=ad(C1M0)，则D0(Ln)=0，D0(Mn)=0，D0(Gr)=C1Gr，结论得证。

4 自同构群

定义ΑutN为自同构群，对任意σ∈AutN和x，y∈N，有

定理3 令σ∈AutN，则存在a，b∈C*和ε∈{±1}满足下列各式:

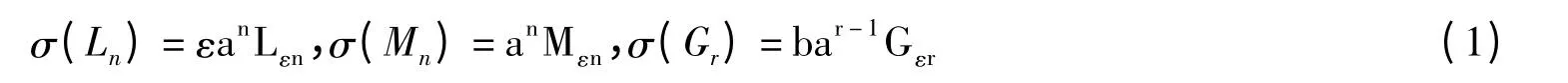
反之，若σ是N 上的一个线性函数满足式(1)，ε∈{±1}和a，b∈C*，则σ∈AutN。

证明 因σ(N0)=N0，设σ(L0)=εL0，σ(Ln)=εanLεn+εan(nc+d)Mεn，σ(Mn)=aneMεn，其中a，e∈C*，c，d∈C[5]。只需考虑σ 作用在Gr上的关系。假设其中，λk∈C*，r1，r2∈Z+将σ 作用在[L0，Gr]= rGr上，有比较Gk系数，得εk=r，即σ(Gr)=λrGεr。将σ 作用在[M0，Gr]=Gr上，得e=1。那么aλr=λr+1，所以设λr=bar-1，b∈C*。再将σ 作用在[Ln，Gr]上，令n=0，得d=0，再观察等式左右，得到c =0。综上，可知σ∈AutN 满足式(1)。定理的另一半证明是显然的。

定义N的自同构σ(ε，a，b)满足式(1)，有σ(ε1，a1，b1)σ(ε2，a2，b2)=σ(ε1ε2，a1ε2a2，b1b2)，σ(ε，a，b)-1=σ(ε，a-ε，b-1)，当且仅当ε1=ε2，a1=a2，b1=b2。

推论 ΑutN=Z2∝(C*×C*)。

5 结束语

研究李超代数的主要动机是这种代数上存在上同调理论，相应的关系式将在物理系统和代数学中有广泛的具体应用和物理解释。上同调问题一直是代数结构与表示论的研究中比较重要的问题之一，对李超代数的结构和表示的研究起重要作用。

[1]Dobrev V K.Characters of the unitarizable highest weight modules over the N =2 superconformal algebras[J].Physics Letters B，1987，186(1):43-51.

[2]孙洪洲，韩其智.李超代数综述[J].物理学进展，1983，3(1):81-125.

[3]Farnsteiner R.Derivations and central extensions of finitely generated graded Lie algebra[J].Journal of Algebra，1988，118(1):33-45.

[4]Liu D，Zhu L.Generalized Heisenberg-Virasoro algebras[J].Frontiers of Mathemat-ics in China，2009，4(2):297-310.

[5]Shen R，Jiang C.The derivation algebra and automorphism group of the twisted Heisenberg-Virasoro algebra[J].Communications in Algebra®，2006，34(7):2 547-2 558.