基于最小轴对称包络域的一元线性回归方法
(中国矿业大学(北京) 管理学院 北京100083)
0 引 言
线性回归分析是数理统计中最基本的研究方法之一,用以研究变量间的相关关系。在社会经济领域,很多变量间的关系即使在宏观上不是线性的,在微观上仍可近似做线性化处理[1-4]。另外,目前主流的统计分析、数值计算软件都以矩阵运算为基础,因此,对变量进行高精度的线性回归具有重要的基础意义。线性回归的方法很多,如简单线性回归[5]、主成分回归[6]等。如果样本点足够多或回归线向方差足够大,各种回归方法都能获得较好的回归效果,但当样本点很少(稀疏数据)且沿实际回归线方向的方差不大时,现有的回归方法的回归误差都经常很大且不容易控制。为解决稀疏数据回归误差较大的问题,本文提出了一种新的线性回归方法,具有坐标无关性及良好的鲁棒性,回归精度及稳定性都明显优于简单线性回归、主成分回归等方法。
1 基于极/最小轴对称包络集的线性回归方法
设有变量x,y 满足线性关系式:

式中,βi(i=0,1)为常数,ε为随机误差。对各变量进行n次观测,观测值以上数据与散点集等价。基于以上观测数据的变量x与y的一元线性回归直线为[5]:

线性回归的误差如图1所示,实线为两个变量实际的函数关系直线,虚线为简单线性回归的结果,由于样本点较少,回归误差很大。

图1 线性回归的误差
若∀a∈S,∃!a'∈S',使得线段aa'被直线L 垂直平分,则称S'为S 关于直线L的镜像对称点集,记作S' =MS(S,L)。
定理1 若L与S的一个主元方向相同,则MS(S,L)与S的主元方向相同。(证明略)
定义2 若MS(S,L)=S,称S为关于直线L的轴对称点集,直线L 称为该轴对称点集的对称轴。
定理2 若MS(S,L)=S,则其对称轴方向与其一个主元方向相同。
定义3 若S为平面内点集,L为同一平面内直线,Sout⊆S,且∀a∈SSout,∃!b∈Sout,使得ab⊥L,且|ao|<|bo|,其中o为ab与L的交点,称Sout为S 相对于L的外侧点子集(Outbound Subset,OS),记作
Sout=OS(S,L)。
定义4 设S为平面内点集,L为同一平面内直线,Sout=OS(S,L),将Sout与MS(Sout,L)中的所有点(统称为角点)按以下规则用一条关于L 对称的闭合折线相连:1)任何一条垂直于L的直线与该闭合折线所围区域的交集要么为空集,要么为一连续线段;2)闭合折线中任意两段线段没有除角点外的其他交点。称以上闭合折线所围区域为S 相对于L的对称包络区域(Symmetrical Envelope Domain,SED),记作SED(S,L),其面积(Area Of Symmetrical Envelope Domain,AOSED)记作AOSED(S,L)。
折线所围的区域SED(S,L)如图2所示。显然,S 相对于L的包络区域为单连通区域。
定义5 设S为平面内点集,Li为同一平面内直线,若AOSED(S,L#)=min{AOSED(S,Li)},称SMSED=SED(S,L#)为S的最小对称包络域(Minimal Symmetrical Envelope Domain,MSED),若不特意指出L#,可简记作SMSED=MSED(S)。L#称为MSED(S)的对称轴,MSED(S)的面积可表示为AOMSED(S)。
定理3 若MSED(S)=SED(S,L#),在满足某收敛条件时,L#的方程y =β#1x+β#0是变量组(x,y)的具有坐标无关性的回归直线的无偏估计。(证明略)
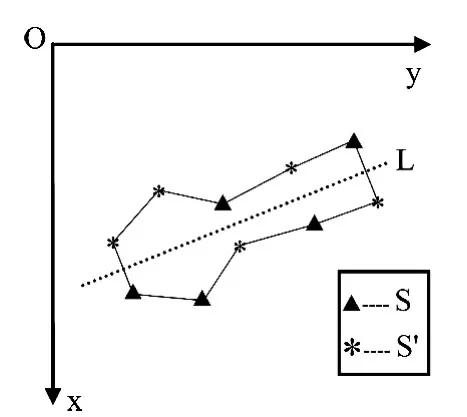
图2 SED(S,L)
定理3中的收敛条件在不同条件下有不同的形式,但一般都不难满足。在一些特殊情况下,(x,y)的回归直线的无偏估计可能对应于函数AOSED(α,β0)=AOSED(S,L)的某极小值点。
综上,可定义以下一种新的线性回归的方法。
定义6 先求取MSED(S),一般情况下,其对称轴就是以S的元素为样本点的变量组(x,y)的具有坐标无关性的回归直线的无偏估计,特殊情况下,函数AOSED(α,β0)的某极小值点对应于回归直线的无偏估计。这种线性回归方法称为基于极/最小轴对称包络域的线性回归方法(Minimal Symmetrical Envelope Domain Regression,MSEDR),简称包络域法。
当S的元素在空间上分布比较密集时,包络域法与主成分回归法的结果基本等价。当S的元素在空间上分布比较稀疏时,包络域法回归结果在稳定性及健壮性上具有优势。
2 仿真实验数据
2.1 算法设计
包络域法作为一种计算解运算量很大,为其设计特殊的高速算法是十分必要的。该方法的计算量主要集中在大量的求取对称包络域的运算,这其中求取点集相对于直线的镜像集更是占用了运算量的绝大部分。本文注意到,当直线的位置比较特殊,例如直线与坐标轴平行时,求取点集相对于直线的镜像只需做某种坐标“变号+平移”运算,运算量大幅度减少。为此,设计了以下算法,将绝大多数求取镜像集的运算转化为“变号+平移”运算,可实现包络域法的快速计算。
1)选择合适的线性回归方法进行回归直线粗定位运算,设运算结果为:

2)指定搜索范围为Ω ={(α,β0')|α∈(α1,α2),β0'∈(β1',β2')},须满足(β1',β2'),其中逆时针旋转角度α0后的对应直线。
3)若α∈(α1,α2),将S 逆时针旋转角度α,S1为S 旋转后的结果如图3所示。使β0'在区间(β1',β2')上遍历,计算AOSED(α,β0')=AOSED(S1,L')。若以S的重心c(X,Y)作为旋转的中心,且旋转后将坐标原点平移到c,坐标变换矩阵为:

SED(S1,L')的边界点连接顺序可这样确定:
①将OS(S1,L')中各点按横坐标升序排序为中各点按横坐标升序排序为
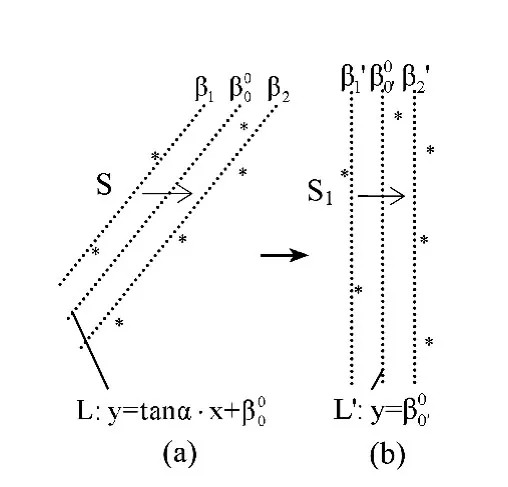
图3 S 旋转前后直线的对应关系
若多边形顶点顺序为(x1,y1),…,(xn,yn),根据向量外积公式,可推导出其面积其中xn+1= x1,yn+1= y1。
4)改变α值,重复步骤3。

2.2 仿真实验
为简化计算,构建的数学模型如图4所示,L为面内直线,5条虚线都垂直于L 且间隔为,5个随机散点分别位于5条虚线上且相对于L的垂直位移服从正态分布,数学描述如下:
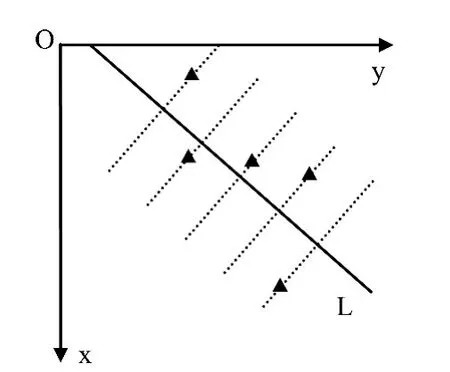
图4 随机产生初始数据
1)设D1,...,D5相互独立,且DiN(0,0.4),di为随机变量Di的观测值,i=1,...,5;
2)x与y为变量,其观测值向量分别为:X=(x1,x2,x3,x4,x5)',Y=(y1,y2,y3,y4,y5)',其中
显然,变量x与y的理论关系式为:

分别用简单线性回归法、主成分分析法、包络域法对以上数据进行回归计算,将计算结果与式(6)比较可得出相应的回归误差。简单线性回归法的回归系数为主成分分析法的回归系数其中
考虑到当回归直线的倾角较大时,其位置的微小变化将引起斜率的剧烈变动,因此将β1作为误差的度量变量并不合适,本文采用回归直线倾角的误差Δα 作为回归误差的度量指标;另外,回归直线的截距β0相对于β1(或α)并不独立,单独讨论其误差并无实际意义;综上,只选取Δα 一个指标来度量各回归方法的表现。对(X,Y)进行30次独立观测并用3种方法进行一元回归,回归直线倾角如表1所示,3种回归方法的平均误差及平均绝对误差如表2所示,其中,为
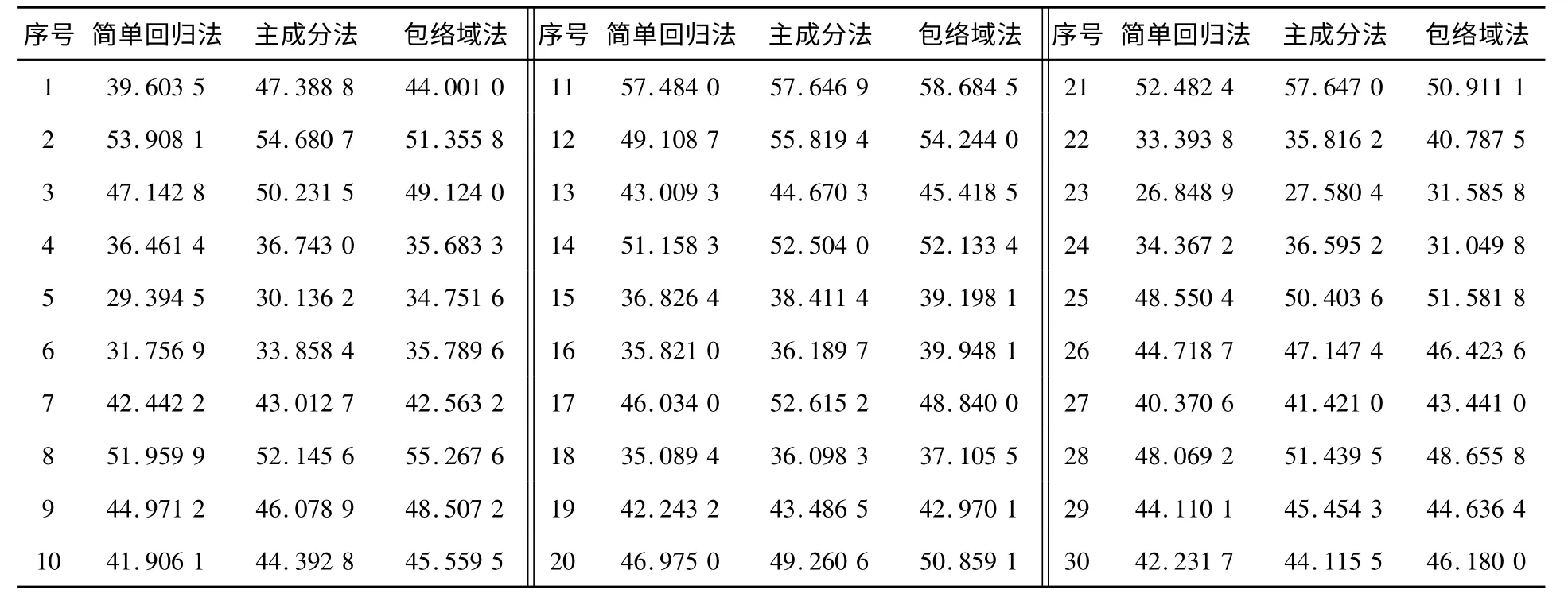
表1 一元线性回归倾角数据汇总表(单位:°)
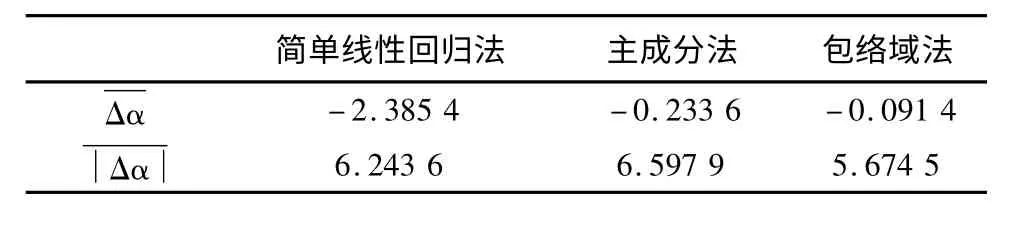
表2 一元线性回归倾角误差数据表(单位:°)
3 结束语
本文仿真实验证明了包络域法在一元线性回归时比主成分法和线性回归法精度更高、更加稳定。包络域法的结果是一种数值解,其计算量比主成分法这样的解析解大得多,但在绝大多数非实时运算的情况下,相对于计算精度的提高,其计算量上的缺点是可以接受的。本文只讨论了包络域法在一重一元线性回归中的应用,其在一重多元、多重多元线性回归中的应用情况还有待进一步的研究。
[1]Xu Weiwei.Risk Conversion of Debt Financing in the Coal Company[C].Zhengzhou:Artificial Intelligence,Management Science and Electronic Commerce,2011:5 142-5 145.
[2]许蔚蔚.基于煤炭企业债务期限结构的回归对比分析[J].会计之友,2011,(11):116-118.
[3]Xu Lili,Liu Shaowei.Establishing Prime System of Financial Management in Rural Enterprise[C].Sydney:Orient Academic Forum,2007:747-751.
[4]Ning Yuncai,Mao Yuyan.The risk monitoring of coal construction project based on system dynamics model[C].New York:Curran Associates,Inc.,2011:330-334.
[5]盛聚,谢式千,潘承毅.概率论与数理统计(第三版)[M].北京:高等教育出版社,2001:297.
[6]于秀林,任雪松.多元统计分析[M].北京:中国统计出版社,1999:156-161,239.

