Chaboche随动硬化模型参数确定及棘轮效应
姜金朋 陈 涛 金 平
(北京航空航天大学 宇航学院,北京100191)
王 珏
(中国运载火箭技术研究院 总体设计部,北京100076)
材料在平均应力非零的应力控制循环载荷作用下会出现塑性应变累积现象,即棘轮效应,这是材料在循环载荷作用下的重要循环塑性行为,对结构循环疲劳起重要作用,因此,准确预测棘轮发展及损伤对结构疲劳分析有重要影响.大部分循环硬化或软化金属达到一定循环次数后稳定,或是屈服面尺寸停止改变,但棘轮仍然增加,因此,随动硬化(屈服面的移动)是棘轮的主要原因.
Hassan,Corona和Kang等人针对材料循环棘轮特性,对不同材料和不同载荷条件进行了大量试验研究[1-6].其中,Hassan 等人[1-4]对碳钢1020、碳钢1026和碳钢1018、不锈钢304进行了较大应力范围的试验,很多研究者采用该文献结果验证模型对棘轮效应预测的准确性.
除了进行试验研究,研究者还提出不同的硬化模型预测材料的循环响应.Prager[7]提出最简单的随动硬化模型,能够反映循环载荷的包辛格效应,但是在描述平均应力非零的应力循环加载时,该模型给出封闭的应力应变滞回环,不能预测棘轮.对Prager硬化律的改进主要有两种:一种是Besseling[8]和 Mroz[9]提出的多面模型,后来又经进一步改进,但是多线性模型仍然不能预测棘轮;另一种改进是考虑逐渐减弱的记忆效应,引入所谓的“恢复项”,Frederick等人[10]最先提出非线性硬化律,Chaboche[11]在此基础上将背应力分解成不同分量,每一个分量遵循A-F硬化律.很多研究表明,Chaboche随动硬化模型能够有效地预测 棘 轮[12-16].Hassan 和 Bari[1,12]等 人 评 估 了Prager,A-F,Chaboche,Ohno-Wang 和 Guionnet 5种本构模型对碳钢棘轮预测的能力,并详细阐述了这些模型预测成功或失败的原因,结果表明,Chaboche和Ohno-Wang模型能很好地预测单轴棘轮.Lynda等人[13]进行了应变控制、应力控制的单轴试验,用Chaboche模型对棘轮效应进行模拟,结果发现,参数优化对得到较好模拟结果有重要作用,Chaboche模型预测单轴棘轮与试验接近.Rezaiee-Pajand等人[14]通过推导背应力演化和塑性应变累积的关系,建立了一套确定Chaboche硬化模型参数的系统数学方法,利用单轴棘轮试验数据确定参数,数值计算结果表明,Chaboche模型非常有效.Mahmoudi等人[15]采用多目标遗传算法计算Chaboche模型参数,同时考虑稳定的应力应变滞回曲线和棘轮曲线,得到的参数用于模型中进行单轴棘轮模拟,结果与试验吻合很好.Badnava等人[16]基于Chaboche随动硬化模型,研究了柱状管在不同加载类型下的循环行为,并且与试验结果符合良好.
本文利用Hassan等人对碳钢CS1026的试验结果,采用单目标遗传算法优化方法,考虑滞回曲线和棘轮曲线,确定3种不同Chaboche模型的参数,并用四分量模型研究加载顺序对棘轮的影响.
1 本构方程
1.1 屈服准则
CHABOCHE随动硬化模型基于Von Mises屈服准则:
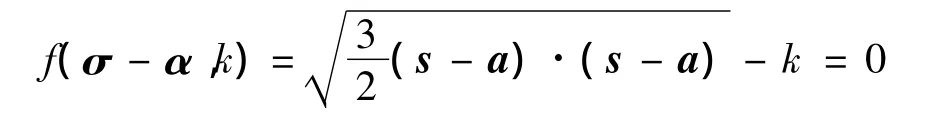
其中,σ为应力张量;α为背应力张量,即屈服面中心;s为偏应力张量;a为偏背应力张量,即偏应力空间中屈服面中心;k为屈服面尺寸,在随动硬化模型中为常数.
1.2 流动准则
描述塑性流动方向,塑性应变在屈服面梯度方向增加:
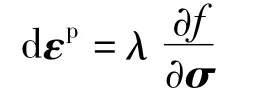
其中,dεp为塑性应变增量;λ为塑性乘子.
1.3 随动硬化律
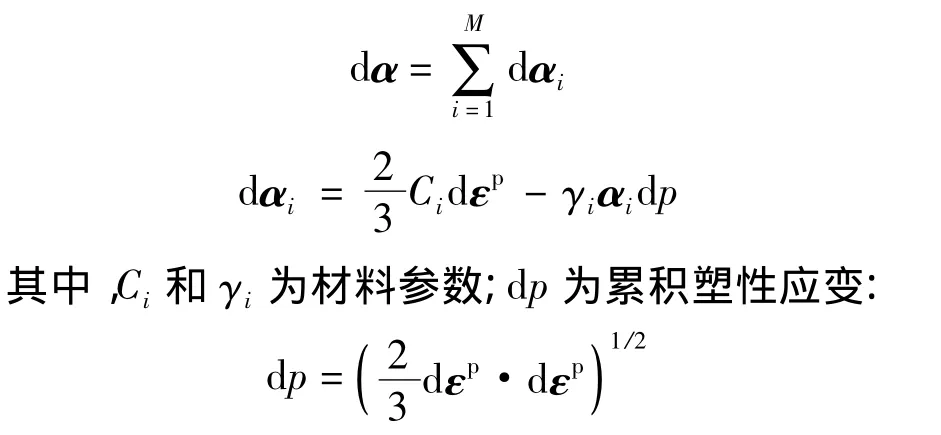
Chaboche硬化模型是几个Armstrong硬化模型的叠加,最初Chaboche提出3个背应力分量(即M=3)的模型,α1用来描述中等塑性应变时的非线性行为,α2用来描述塑性应变非常小的弹塑性过渡区的非线性行为,α3用来描述大塑性应变时的近似常切线刚度现象和极限棘轮应变的非线性行为,屈服面中心αx=α1+α2+α3.
2 Chaboche模型参数确定
由于Chaboche模型中参数较多,而且没有明显的物理意义,因此很难从试验数据中直接获得参数.本文采用单目标遗传算法优化方法,以应变控制循环加载试验得到的稳定应力应变滞回曲线(图1)和应力控制循环加载棘轮试验得到的应变峰值(每一次循环中的最大应变)vs循环次数曲线(图2)[5]的数据为输入,试验中应变控制的循环载荷和应力控制的循环载荷分别如图3、图4所示,图中,σm为平均应力,σa为应力幅值,应力控制的循环加载试验有6组,载荷取值水平如表1所示,优化算法中用作输入的是第2组;Chaboche随动硬化模型参数为输出,使预测的滞回曲线和棘轮曲线与试验的差距最小,目标函数如下式:



图1 应变循环加载试验稳定滞回曲线Fig.1 Hysteresis loop under strain controlled cyclic loading
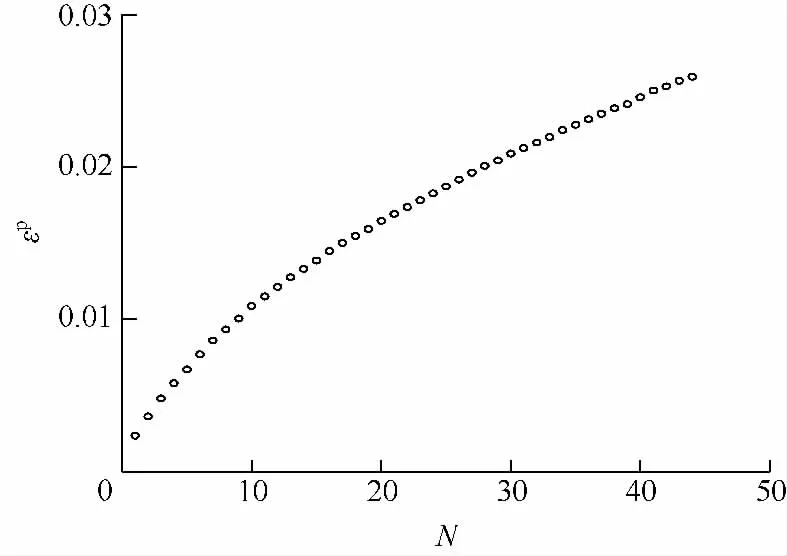
图2 试验应变峰值vs循环次数Fig.2 Experimental peak strain vs cyclic number
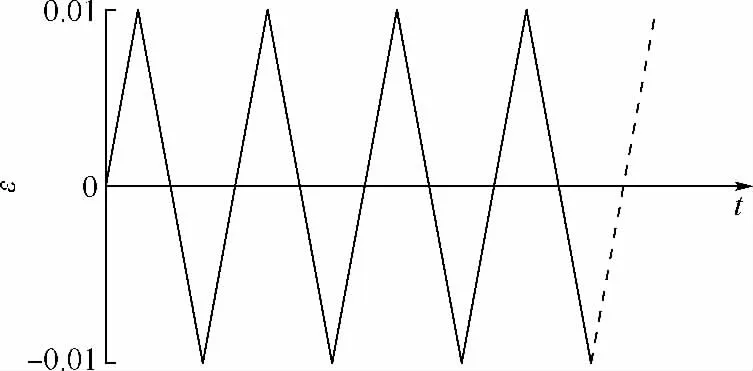
图3 应变控制的循环载荷Fig.3 Strain controlled cyclic loading

图4 应力控制的循环载荷Fig.4 Stress controlled cyclic loading
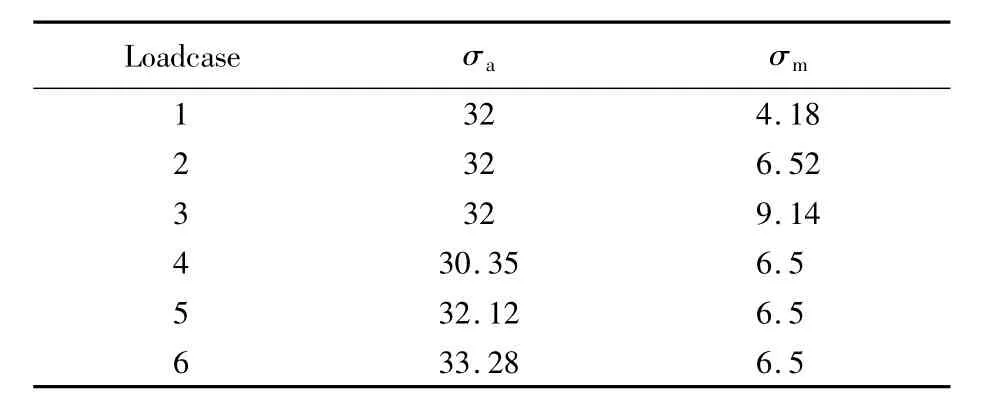
表1 应力控制循环加载试验取值水平Table 1 Mean stress and stress amplitudes in experiments psi
本文采用3种Chaboche模型,包括3个非线性背应力分量的模型(N3L0)、3个非线性分量和1个线性分量的模型(N3L1)以及4个非线性分量的模型(N4L0),通过遗传算法优化得到的模型参数如表2所示.所得Chaboche模型预测的滞回曲线如图5所示,从图中可以看出,3个模型对高应变范围的线性段预测与试验曲线基本一致;N3L0与N4L0模型预测的滞回曲线基本相同,对非线性过渡段预测结果与试验相差较大;N3L1模型在非线性过渡段的预测与试验基本相符,但在开始屈服段预测的应力值比试验结果稍低.
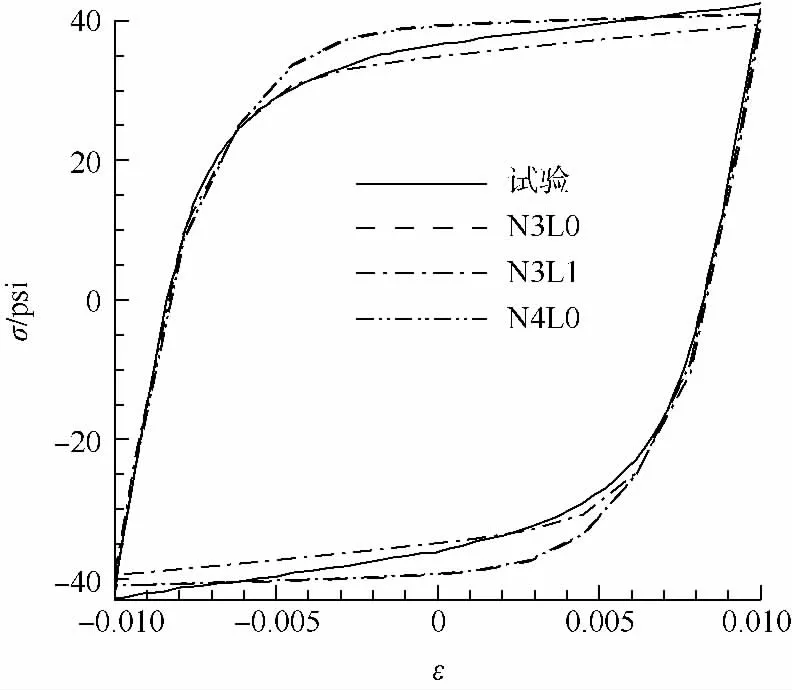
图5 应变控制的滞回曲线Fig.5 Strain controlled hysteresis loop
图6为3个模型预测的棘轮效应与试验结果的比较,可以看出,N3L0模型预测的应变峰值总体上比试验值偏大,Loadcase1和4结果与试验接近,Loadcase2和5的二十几次循环结果与试验吻合,后面的循环预测结果比试验大,可能是由于未考虑到循环硬化的影响,本文以Loadcase2的试验结果为优化输入,得到的模型预测Loadcase3和6结果与试验相差大;N3L1模型预测结果总体上比试验值低,这是因为模型中增加的线性项减弱了模型对棘轮的预测,因此Loadcase1~6的前十几次或三十几次循环预测结果与试验相符,而后面循环的预测值比试验低;N4L0模型预测结果除了Loadcase3比试验结果大,其他与试验结果吻合较好.

表2 CS1026的Chaboche模型参数Table 2 Material parameters of CS1026 in Chaboche model

图6 应变峰值vs循环次数Fig.6 Peak strain vs cyclic number
3 棘轮模拟
从图6可以看出,随着应力平均值或应力幅值增大,每一次循环中的应变峰值增大,近线性段斜率增大,表明应变累积速度增加.为研究加载顺序对棘轮的影响,采用上文中确定的四分量Chaboche模型N4L0对不同加载水平下的棘轮进行模拟.
对低-高、高-低两种不同的加载顺序分别进行棘轮模拟,应力取值水平如表3所示.每一应力水平进行10次循环加载,其中,先加载的应力平均值和应力幅值记为σm1,σa1,后加载的应力平均值和应力幅值记为σm2,σa2.Loadcase1~6中应力幅值一致,低应力水平的应力平均值相同,高应力水平的应力平均值取3组不同大小的值,棘轮模拟结果如图7所示,可以看出,加载顺序低-高的累积应变高于高-低加载的累积应变,而且,高应力水平的平均应力取值越大,两种加载顺序的累积应变相差越多;后加载的低水平应力下棘轮曲线斜率明显低于先加载的低水平应力下的斜率,说明前者的应变累积速度明显低于后者;比较Loadcase2,4,6的低平均应力水平加载可以看出,随着高应力水平的平均应力增大,低应力水平加载的棘轮曲线斜率变小,应变累积减小,Loadcase6甚至基本没有应变累积;图7表明,平均应力加载顺序影响棘轮应变累积,后加载的平均应力水平会受到先前加载应力水平的限制,先加载的平均应力水平越高,后加载的应力受限越明显,应变累积越小.Loadcase7~12中应力平均值一致,低应力水平的应力幅值相同,高应力水平的应力幅值取3组不同大小的值,棘轮模拟结果如图8所示,两种加载顺序下的累积应变几乎相同,说明应力幅值加载顺序对棘轮应变累积的影响小.

表3 应力取值水平Table 3 Mean stress and stress amplitudes psi

图7 应力平均值改变时加载顺序对棘轮的影响Fig.7 Influence of mean stress sequence on ratcheting
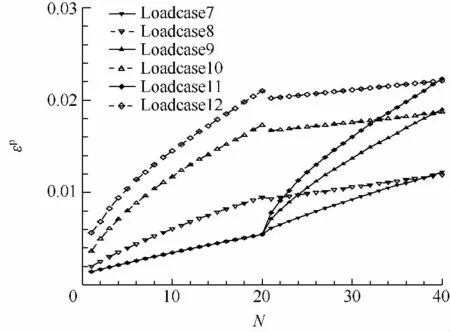
图8 应力幅值改变时加载顺序对棘轮的影响Fig.8 Influence of stress amplitude sequence on ratcheting
4 结论
本文采用遗传算法优化方法,利用文献中CS1026试验的应力应变滞回曲线和棘轮曲线获得Chaboche模型中的参数,并用包含4个随动硬化分量的模型进行棘轮模拟,研究加载顺序对棘轮的影响,得到以下结论:
1)利用试验的应力应变滞回曲线和棘轮曲线,采用遗传算法优化方法,可以有效地确定Chaboche随动硬化模型参数,3种模型中,N4L0模型对棘轮的预测与试验结果吻合最好.
2)增大应力幅值或应力平均值,都会使应变峰值增大,且应变累积速度加快;平均应力加载顺序对累积应变有较大影响,加载顺序高-低的累积应变低于加载顺序低-高的累积应变,而且先加载的平均应力越大,后加载的载荷产生的累积应变越小;而应力幅值加载顺序对应变累积几乎没有影响.
References)
[1] Hassan T,Kyriakides S.Ratcheting in cyclic plasticity,part I:uniaxial behavior[J].International Journal of Plasticity,1992,8(1):91-116
[2] Hassan T,Corona E,Kyriakides S.Ratcheting in cyclic plasticity,part II:multiaxial behavior[J].International Journal of Plasticity,1992,8(2):117-146
[3] Hassan T,Kyriakides S.Ratcheting of cyclically hardening and softening materials:I.uniaxial behavior[J].International Journal of Plasticity,1994,10(2):149-184
[4] Hassan T,Kyriakides S.Ratcheting of cyclically hardening and softening materials:II.multiaxial behavior[J].International Journal of Plasticity,1994,10(2):185-212
[5] Corona E,Hassan T,Kyriakides S.On the performance of kinematic hardening rules in predicting a class of biaxial ratcheting histories[J].International Journal of Plasticity,1996,12(1):117-145
[6] Kang G Z,Gao Q,Yang X J.Uniaxial cyclic ratcheting and plas-tic flow properties of SS304 stainless steel at room and elevated temperatures[J].Mechanics of Materials,2002,34(3):145-159
[7] Prager W.A new method of analyzing stresses and strains in work-hardening plastic solids[J].ASME Journal of Applied Mechanics,1956,23:493-496
[8] Besseling J F.A theory of elastic,plastic,and creep deformations of an initially isotropic material showing anisotropic strain-hardening,creep recovery and secondary creep[J].ASME Journal of Applied Mechanics,1958,25:529-536
[9] Mroz Z.On the description of anisotropic work-hardening[J].Journal of the Mechanics and Physics of Solids,1967,15:163-175
[10] Frederick C O,Armstrong P J.A mathematical representation of the multiaxial bauschinger effect[J].Materials at High Temperatures,2007,24(1):1-26
[11] Chaboche J L.Time-independent constitutive theories for cyclic plasticity[J].International Journal of Plasticity,1986,2(2):149-188
[12] Bari S,Hassan T.Anatomy of coupled constitutive models for ratcheting simulation[J].International Journal of Plasticity,2000,16(3/4):381-409
[13] Lynda D,Salim M.Performance of the Chaboche kinematic hardening modelto predictratchetusing differentdata bases[J].International Review of Mechanical Engineering,2009,3(4):467-472
[14] Rezaiee-Pajand M,Sinaie S.On the calibration of the Chaboche hardening model and a modified hardening rule for uniaxial ratcheting prediction[J].International Journal of Solids and Structures,2009,46(16):3009-3017
[15] Mahmoudi A H,Pezeshki-Najafabadi S M,Badnava H.Parameter determination of Chaboche kinematic hardening model using a multi objective genetic algorithm[J].Computational Materials Science,2011,50(3):1114-1122
[16] Badnava H,Farhoudi H R,Nejad K F,et al.Ratcheting behavior of cylindrical pipes based on the Chaboche kinematic hardening rule[J].Journal of Mechanical Science and Technology,2012,26(10):3073-3079

