基于三维最小二乘方法的空间直线度误差评定

王炳杰 赵军鹏 王春洁*，2

(1.北京航空航天大学 机械工程及自动化学院，北京100191;2.北京航空航天大学 虚拟现实技术与系统国家重点实验室，北京100191)

直线度误差是评定机械产品精度的重要指标之一，并且也是平行度、垂直度、圆柱度和同轴度等几何测量的基础［1］.国标 GB/T 11336—2004中的空间直线度误差评定方法有:最小包容区域法、最小二乘法和两端点连线法［2］.最小包容区域法为精确算法，其评定结果小于或等于其他两种评定方法，但是该方法求解复杂.目前针对最小包容区域法的求解已经发展了遗传算法［3］、坐标转换原理［4］、半定规划算法［5］、平面投影算法［6］、准粒子群优化算法［7］以及组合优化算法［8］等.在实际工程检测中常用两端点连线法与最小二乘法(LSM，Least Squares Method)，这两者均属于近似算法，其中两端点连线法的鲁棒性较差，LSM算法的数学模型在原理上存在缺陷［9］，该方法由于在最小二乘中线拟合时分别在两个平面上独立拟合直线，再合成空间直线，因此不是真正的三维空间直线拟合.当测量点坐标值的数量级不同时，LSM算法的评定结果不能满足精度要求高的实际工程的要求.

最小二乘法评定空间直线度误差的关键是准确拟合测点的最小二乘中线，其涉及到非线性规划问题的求解，通常采用优化算法求解［1］.非线性规划优化算法的缺点是需要迭代计算并且难以得到全局最优解.针对此问题一些学者提出了无迭代算法［10］、LSABC 算法［11］、改进的 LSABC 算法［12］以及3DLSA 算法［13］等.这些算法虽然完善了空间直线度误差评定方法，但是空间直线度误差是一种复杂的形状误差，其评定算法仍然值得探索.本文采用三维最小二乘方法建立了空间直线拟合的数学模型，给出了该数学模型的精确解，基于新解法提出空间直线度误差评定新方法，并用数值算例验证了新方法的有效性.

1 空间直线度误差评定数学模型

1.1 空间直线拟合

按最小二乘法评定空间直线度误差，首先需要进行测点的最小二乘中线拟合，得到测点最小二乘中线Lf.最小二乘中线是指使实际直线上各点到该直线的距离平方和为最小的一条理想直线［2］.如图 1，设(x1，y1，z1)，…，(xk，yk，zk)为 k 个直线度测量点，直线Lf的方向向量为(l，m，n)且通过点(x0，y0，z0)，则 Lf的方程为

为了方便起见，单位化直线Lf方向向量使l2+m2+n2=1.

图1 最小二乘法评定直线误差度示意图Fig.1 Diagram of spatial straightness error evaluation with LSM

根据最小二乘原理，使得各测量点到拟合直线距离的平方和最小:

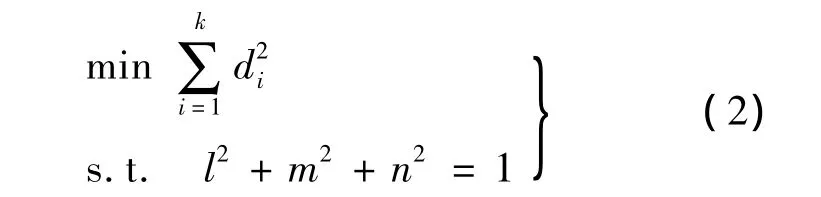
其中 di为测量点(xi，yi，zi)到拟合直线距离:

为了求解该优化问题，首先证明直线Lf一定通过各测量点的重心()，其中:

且当［l，m，n］T为矩阵 B 的最大特征值 λmax(B)对应的单位特征向量时式(12)可以取最小值.因此为了求解测点最小二乘中线Lf的方向矢量，只需要求解矩阵B的最大特征值对应的单位特征向量即可.

1.2 最小包容圆柱面直径求解

为了求解测点的最小包容圆柱面直径，通过空间投影将测点向垂直于最小二乘拟合直线Lf的平面投影，将空间问题转化为平面问题.显然投影点点集在该平面上的最小包容圆直径等于拟合直线最小包容圆柱面直径.为简化最小包容圆直径计算，在投影平面上构建局部坐标系并进行坐标变换，将投影点在空间坐标下的坐标转化为在局部平面坐标系中的坐标(Xi，Yi).假设Xmax=maxXi，Xmin=min Xi，Ymax=max Yi，Ymin=min Yi(i=1，2，…，k).采用格点法寻找最小包容圆直径.如图 2所示，将矩形区域 Xmin≤X≤Xmax，Ymin≤Y≤Ymax的横纵坐标均划分成N等份，从而得到(N+1)×(N+1)个结点，依次计算每一结点与投影点集中点的最大距离Dmaxpq(p=0，1，…，N;q=0，1，…，N)，则 Dmaxpq中的最小值即为最小包容圆半径R.最小包容圆柱面直径φf=2R即为空间直线度误差值.

2 数值实验与结果分析

图2 搜索区间节点Fig.2 Nodes in search interval

根据上述算法，利用Matlab R2008编写空间直线度误差评定程序.参考文献中测点数据进行数值实验，结果见表1.

表1 计算结果Table 1 Calculation results

计算结果显示新算法评定空间直线度误差时，可以得到2个或3个测量点与最小二乘中线包容圆柱面相接触，满足国家标准的要求［2］.因此该算法是一种有效的评定空间直线度误差的算法.

表1中的测量点分为3类:

1)文献［4］测量点数值数量级不同，LSM算法结果为771 845.670 0，3DLSA算法得出的结果为7.2448，本文方法结果为6.2399;

2)文献［3］与文献［6］测量点数值数量级相同，LSM算法结果分别为18.100 0和30.000 0，3DLSA算法结果分别为13.500 0和36.300 0，本文方法结果分别为9.9764和28.4760;

3)文献［15］与文献［5］中测量点坐标相对差值相同，只是调换了坐标轴次序，它们的空间直线度误差值应该相同，但是LSM算法的评定结果相差较大，3DLSA算法满足此要求，本文方法亦满足此要求，而且本文方法评定的直线度误差值更小.

由此可知，本文方法是一种更加准确稳健的直线度误差评定方法.

本文方法评定结果的误差大小只与搜索区间的划分精度有关，搜索区间划分越细密精度越高.本文数值实验将搜索区间细分成1001×1001个结点，计算机运算时间不超过3 s.

3 结论

1)本文采用三维最小二乘方法建立了空间直线拟合的数学模型，并给出了该数学模型的精确解，完善了空间直线拟合的理论基础.

2)本文方法相较于算例中提及的算法具有更好的稳定度和准确度.

3)本文方法计算效率较高可应用于精密测量以及数据处理中.

References)

［1］张新宝，谢江平.空间直线度误差评定的逼近最小包容圆柱法［J］.华中科技大学学报:自然科学版，2011，39(12):6-9 Zhang Xinbao，Xie Jiangping.Evaluating spatial straightness errorby approaching minimum enclosure cylinder［J］.Journal of Huazhong University of Science and Technology:Natural Science Edition，2011，39(12):6-9(in Chinese)

［2］GB/T 11336—2004 直线度误差检测［S］GB/T 11336—2004 Measurement of departures from straightness［S］(in Chinese)

［3］廖平，喻寿益.基于遗传算法的空间直线度误差的求解［J］.中南大学学报:自然科学版，1998，29(6):586-588 Liao Ping，Yu Shouyi.A method of calculating 3-D line error using genetic algorithms［J］.Journal of Central South University:Science and Technology，1998，29(6):586-588(in Chinese)

［4］李淑娟，刘云霞.基于坐标变换原理的最小区域法评定空间直线度误差［J］.计测技术，2006，26(1):24-25 Li Shujuan，Liu Yunxia.A method for minimum zone evaluation of space linearity error based on principle of coordinate transformation［J］.Metrology ＆ Measurement Technology，2006，26(1):24-25(in Chinese)

［5］ Ding Y，Zhu L M，Ding H.Semidefinite programming for chebyshev fitting of spatial straight line with applications to cutter location planning and tolerance evaluation［J］.Precision Engineering，2007，31(4):364-368

［6］黄富贵，崔长彩.任意方向上直线度误差的评定新方法［J］.机械工程学报，2008，44(7):221-224 Huang Fugui，Cui Changcai.New method for evaluating arbitrary spatial straightness error［J］.Chinese Journal of Mechanical Engineering，2008，44(7):221-224(in Chinese)

［7］ Wen X L，Xu Y X，Li H S，et al.Monte Carlo method for the uncertainty evaluation of spatial straightness error based on new generation geometrical product specification［J］.Chinese Journal of Mechanical Engineering，2012，25(5):875-881

［8］ Endrias D H，Feng H Y，Ma J，et al.A combinational optimization approach for evaluating minimum-zone spatial straightness errors［J］.Measurement，2012，45(5):1170-1179

［9］胡仲勋，杨旭静，金湘中.LSM算法评定空间直线度误差的分析与改进［J］.湖南大学学报:自然科学版，2010，37(2):27-31 Hu Zhongxun，Yang Xujing，Jin Xiangzhong.Analysis and improvement of the LSM algorithm for assessing spatial straightness error［J］.Journal of Hunan University:Natural Sciences，2010，37(2):27-31(in Chinese)

［10］郭际明，向巍，尹洪斌.空间直线拟合的无迭代算法［J］.测绘通报，2011(2):24-25 Guo Jiming，Xiang Wei，Yin Hongbin.Three-dimensional line fitting without iteration［J］.Bulletin of Surveying and Mapping，2011(2):24-25(in Chinese)

［11］胡仲勋，杨旭静，王伏林.空间直线度误差评定的LSABC算法研究［J］.工程设计学报，2008，15(3):187-190 Hu Zhongxun，Yang Xujing，Wang Fulin.Research on LSABC algorithm for evalution of spatial straightness error［J］.Journal of Engineering Design，2008，15(3):187-190(in Chinese)

［12］胡仲勋，王伏林，周海萍.空间直线度误差评定的新算法［J］.机械科学与技术，2008，27(7):879-882 Hu Zhongxun，Wang Fulin，Zhou Haiping.A new algorithm for evaluation of spatial straightness error［J］.Mechanical Science and Technology for Aerospace Engineering，2008，27(7):879-882(in Chinese)

［13］胡仲勋，杨旭静，金湘中.评定空间直线度误差的3DLSA算法研究［J］.中国机械工程，2010，21(3):325-329 Hu Zhongxun，Yang Xujing，Jin Xiangzhong.Research on 3DLSA for evaluating spatial straightness errors［J］.China Mechanical Engineering，2010，21(3):325-329(in Chinese)

［14］张筑生.数学分析新讲(第二册)［M］.北京:北京大学出版社，1990:294-295 Zhang Zhusheng.New lecture of mathematical analysis(book two)［M］.Beijing:Peking University Press，1990:294-295(in Chinese)

［15］ Wen X L，，Song A G.An improved genetic algorithm for planar and spatial straightness error evaluation［J］.International Journal of Machine Tools ＆ Manufacture，2003，43(11):1157-1162