典型壁板搭接区试验件疲劳寿命分析

龚思楚，张宪政，杜兴刚，江 鹏，王 震

（中航工业洪都，江西 南昌330024）

0 引 言

在现代飞机机体结构中， 最常用的连接形式就是铆接连接[1]。 试验表明，在疲劳载荷作用下，机体结构疲劳裂纹的萌生和扩展多半发生在这类连接结构件的细节处[2]。 疲劳破坏是飞机结构失效的主要形式，结构疲劳寿命也是飞机寿命的一个重要指标。

连接件的受载形式、孔的布置、孔径、紧固件和板件的材料、装配方法、表面处理及局部应力应变分布等因素决定了紧固件连接结构细节的疲劳品质。经分析可知， 结构的细节疲劳品质可以综合成应力严重系数这一参数描述[3]。

紧固件连接有限元仿真分析主要有用梁单元模拟，并耦合自由度；采用多个弹簧元来模拟，设置弹簧元的刚度系数以及采用三维实体建模， 设置接触三种方法[4]。

三维有限元模型能相对真实的反映结构的变形状态。 尤其是弯曲和次弯曲对应力集中的影响[5、6]，因此本文通过对典型壁板搭接区建立三维实体有限元模型进行应力分析，运用有限元分析、应力严重系数法和线性损伤累积理论对典型壁板搭接区试验件在随机载荷谱作用下的疲劳特性进行分析计算， 计算结果满足目标寿命要求。

1 有限元分析

由于试验件横向对称，在有限元模型中，为简化计算，根据结构对称情况，取一半建立有限元模型，并在对称面处建立对称约束。

典型壁板搭接区结构数模如图1 所示， 两块壁板通过沉头铆钉连接（铆钉牌号Q/5A996-5)，整体尺寸为500×172.8mm； 壁板和铆钉的材料属性为弹性模量E=71000 MPa，泊松比υ=0.33。

壁板试验件有限元模型中一端施加固支约束，另一端施加轴向载荷50 kN。

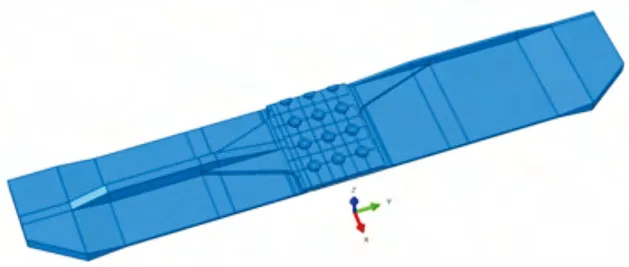
图1 搭接区结构图

图2 显示了壁板试验件沿厚度方向的位移云图，变形放大20 倍，从图2 看出两块壁板中间区域发生向下的弯曲变形， 而且筋条处向下弯曲最为严重，靠近搭接区。

图2 厚度方向位移（U3）云图

图3 显示了搭接区壁板钉孔应力云图， 从图3中可以看到最大应力发生在内壁板第一排第一列钉孔表面处。 最大应力σref=627.3MPa。 由此可知，第一排第一列的钉传载荷最大。

图3 内壁板钉孔应力云图

2 疲劳寿命预估

试验件的疲劳寿命估算值采用工程上普遍应用的应力严重系数法 （SSF）， 并在此基础上采用Miner 线性损伤累积理论估算出试验件的疲劳寿命。通过编辑计算程序实现对材料不同应力严重系数下的S-N 曲线进行插值， 估算出载荷谱下模拟件的疲劳寿命。

2.1 疲劳分析方法基本流程（图4）

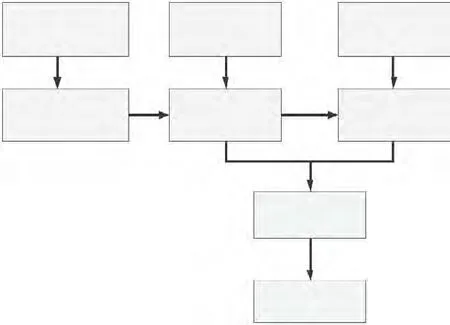
图4 疲劳分析流程图

2.2 疲劳分析具体实现

按照图4 中所示的基本分析流程编写Fortran 程序，自动读入给定的载荷谱的峰值、谷值以及频次，计算该载荷下的损伤累积量， 最后可直接输出疲劳寿命。 下面对其中的具体细节处理给出说明：

1）应力严重系数

由上述有限元计算可知， 最大应力发生在内壁板第一排第一列钉孔下表面处， 最大应力σref=627.3MPa。 内壁板第一排孔的净截面面积Anet=227.81mm2， 当外载荷为F=50kN 时第一排孔截面的名义应力σnom=F/Anet，应力严重系数：

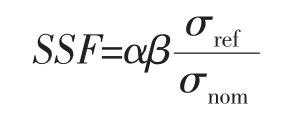
其中，α 表示孔表面状态系数，β 表示孔填充系数，试验件钻孔(α=1.1)，铆接(β=0.75)。 经计算得到应力严重系数为SSF=2.3579。

2）应力谱

Fortran 程序自动读入随机载荷谱， 有限模型中施加的载荷是F=50kN，产生的最大应力为σref=627.3MPa，若飞行剖面中的一个随机载荷值为Frandom， 则该随机载荷值对应的应力为

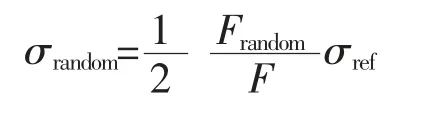
上式中，系数1/2 是因为有限元模型是半宽度模型。 按照上式关系，可得到整个加载周期内的应力谱。

3）SSF 的等寿命曲线

对于7475-T7351 铝，通过手册可以查询到Kt=1和Kt=3 的S-N 曲线，如图5、图6 所示，它们的拟合公式分别是：

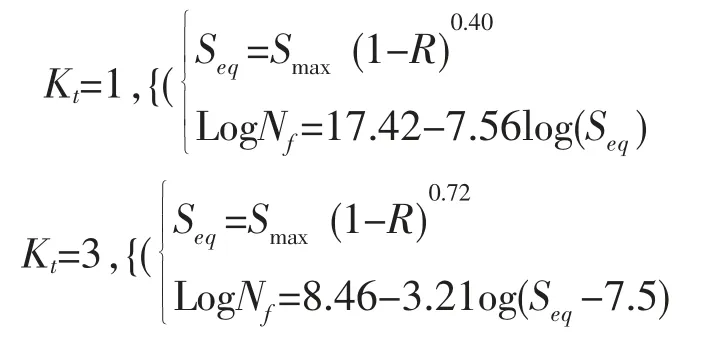
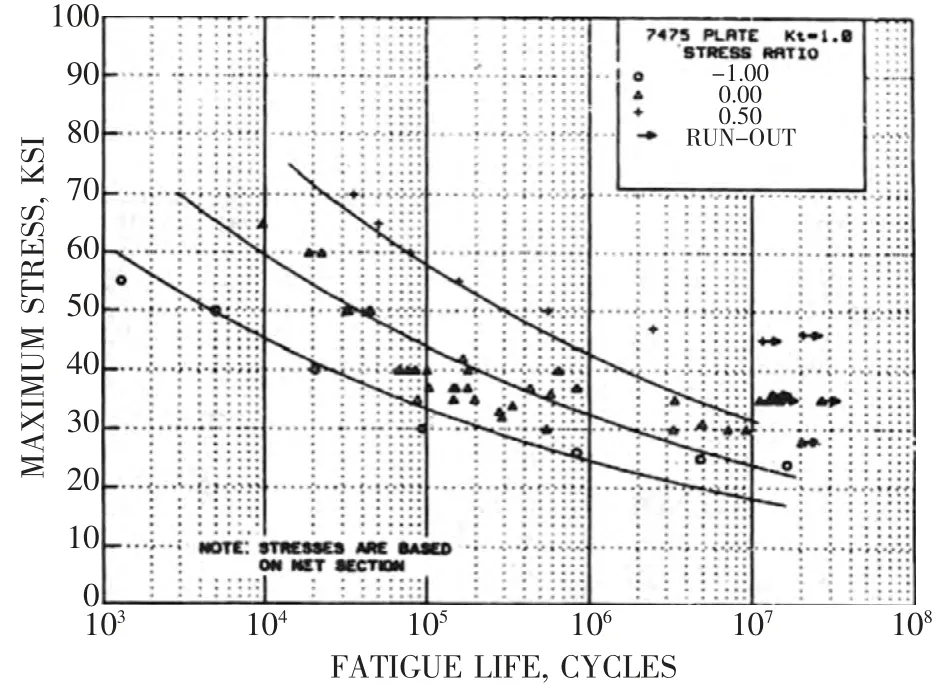
图5 7475-T7351 铝板在Kt=1 时，应力比R 为-1.0,0.0,0.5 最佳拟合S/N 曲线

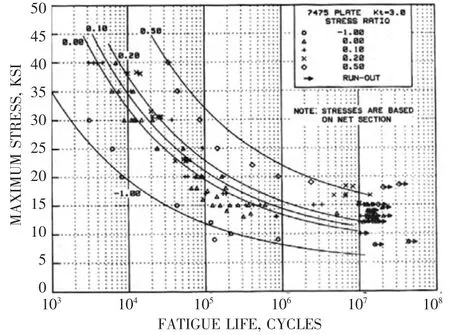
图6 7475-T7351 铝板在Kt=3 时，应力比R 为-1.0,0.0,0.1,0.2,0.5 最佳拟合S/N 曲线

上述拟合公式存在适用范围， 对于不在适用范围内的情况一律按照插值推得到。

4）Miner 线性疲劳累积损伤量

线性疲劳损伤累积理论指在循环载荷作用下，疲劳损伤是可以线性累积的， 当累加的损伤达到某一数值时，试件或构件就发生疲劳破坏。 一个循环造成的损伤量是

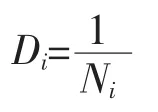
式中Ni为对应于当前载荷水平下的疲劳寿命。变幅载荷下，n个循环造成的损伤是

当损伤累积到1 时，Miner 理论认为结构发生疲劳破坏。

计算整个循环周期得到损伤累积， 考虑分散系数，根据下式计算出疲劳寿命；

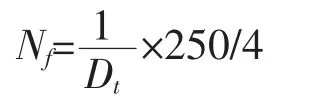
5）寿命估算结果

按照上述过程编辑Fortran 计算程序。 最终计算寿命为Nf=29951（飞行小时，考虑分散系数4），即2.9倍设计寿命，满足结构目标寿命。

6）试验对比

对典型壁板搭接区试验件进行疲劳耐久性试验， 在耐久性试验中， 在随机载荷谱下进行疲劳试验，在4 倍设计寿命期内未发生疲劳裂纹，与分析结果吻合较好，达到了预期疲劳寿命指标。

3 结 论

根据计算结果，可得出以下结论：

1）通常采用板和梁建立简化的有限元模型，提取钉载荷旁路载荷的方法计算最大应力， 进而算出应力严重系数， 而本文采用建立三维实体有限元模型的方法得到最大应力和应力严重系数。 三维有限元模型将更真实的反映结构的变形状态。 通过与模拟件的疲劳耐久性试验进行对比， 试验结果与分析结果吻合较好； 体现出了对搭接件进行三维实体有限元分析的优越性。

2）Miner 理论不考虑加载次序对疲劳寿命的影响，而实际上加载次序对疲劳寿命的影响很大，由于过载造成的超载迟滞效应也会增加疲劳寿命， 所以本文计算得到的结构疲劳寿命是偏保守的。

[1]姚卫星. 结构疲劳寿命分析. 北京: 国防工业出版社，2003.

[2]刘文珽等. 结构可靠性设计手册. 国防工业出版社，2008.

[3]中国航空研究院. 军用飞机疲劳；损伤容限，耐久性设计手册（第二册）—疲劳设计.

[4]王旭. 机翼下壁板螺栓连接疲劳寿命分析，航空计算技术. 西安:西北工业大学，2010.

[5]ABAQUS6.11User,Manual,ABAQUSInc,Province,RI,USA.2011.

[6]庄茁，张帆，岑松. ABAQUS 非线性有限元分析与实例. 北京:科学出版社，2005.

[7]Metallic materials and elements for aerospace vehicle structures, Department Of Defense Handbook,MIL-HDBK-5J,31 January 2003.